Управление амплитудой волн, вызванных донными смещениями
Аннотация
В этой статье был предложен метод управления амплитудами волн, вызванных смещениями дна, в плоскости рассмотрена задача о волновом движении идеальной однородной жидкости.
Ключевые слова: Управление амплитудами волн, возмущениями дна, идеальной однородной жидкости, интегральное преобразование, уравнению неразрывности, свободная поверхность.05.13.18 - Математическое моделирование, численные методы и комплексы программ
В последние годы существенно возросло число хозяйственных объектов, располагающихся у побережья морей и океанов, и, следовательно, подверженных катастрофическому воздействию волн. Значительная часть этих объектов характеризуется высокой степенью риска как в период их возведения так и, главным образом, в период эксплуатации.
В работе предложен метод управления амплитудами волн, вызванных донными смещениями.
-
Постановка задачи. В плоской постановке рассматривается задача о волновом движении идеальной однородной жидкости, вызванном возмущениями дна, поверхностными активными напряжениями и начальными условиями. возмущения дна .
![]()
![]()
![]() (1)
(1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Здесь,![]()
![]() - компоненты скорости частиц жидкости,
- компоненты скорости частиц жидкости, ![]() - динамическая часть гидродинамического давления,
- динамическая часть гидродинамического давления,![]() - возвышение свободной поверхности,
- возвышение свободной поверхности, ![]() - глубина жидкости,
- глубина жидкости, ![]() - плотность жидкости,
- плотность жидкости, ![]() - ускорение свободного падения,
- ускорение свободного падения, ![]() - коэффициент поверхностного напряжения [1],
- коэффициент поверхностного напряжения [1], ![]() - внешнее активное напряжение, действующее на свободной поверхности водоема,
- внешнее активное напряжение, действующее на свободной поверхности водоема, ![]() - заданная скорость смещения дна водоема,
- заданная скорость смещения дна водоема, ![]() - начальная деформация свободной поверхности жидкости,
- начальная деформация свободной поверхности жидкости,![]() - начальные скорости частиц жидкости,
- начальные скорости частиц жидкости,![]() - время,
- время, ![]()
![]() - координаты.
- координаты.
Начало координат взято на невозмущенной поверхности жидкости, ось![]() - направлена вертикально вверх против силы тяжести, ось
- направлена вертикально вверх против силы тяжести, ось![]() - направлена по горизонтали, в горизонтальных направлениях жидкость простирается до бесконечности.
- направлена по горизонтали, в горизонтальных направлениях жидкость простирается до бесконечности.
2. Интегральная форма решения. Применим к задаче (1) интегральное преобразование Лапласа по времени ![]() , и экспоненциальное преобразование Фурье по переменной
, и экспоненциальное преобразование Фурье по переменной![]() [2].
[2].
Здесь ![]() - параметр преобразования Лапласа,
- параметр преобразования Лапласа, ![]() - параметр преобразования Фурье,
- параметр преобразования Фурье,![]() - двойное преобразование Лапласа и Фурье
- двойное преобразование Лапласа и Фурье ![]() функции . Получим:
функции . Получим:
![]()
![]()
![]() (2)
(2)
![]()
![]()
![]()
![]()
![]()
В процессе применения интегральных преобразований учтены начальные условия и условия на бесконечности по ![]() (1).
(1).
Первое уравнение системы (2) умножим на![]() , второе продифференцируем по
, второе продифференцируем по ![]() и сложим их. При этом учтем, что начальное поле скорости удовлетворяет уравнению неразрывности:
и сложим их. При этом учтем, что начальное поле скорости удовлетворяет уравнению неразрывности:
![]() , и поэтому
, и поэтому![]() .
.
Имеем:
![]() ,
,![]() .
.
Здесь![]() ,
, ![]() - неизвестные постоянные, которые надо найти из граничных условий.
- неизвестные постоянные, которые надо найти из граничных условий.
Из первого и второго уравнений системы (2) находим:
![]()
![]() (3)
(3)
Далее имеем:![]()
![]()
Подставляем найденные выражения для ![]()
![]()
![]() в граничные условия системы (2), получим систему уравнений для определения
в граничные условия системы (2), получим систему уравнений для определения![]() и
и
![]() :
:

![]()
![]() (4)
(4)
Вычислим основной определитель![]() этой системы. Имеем:
этой системы. Имеем:
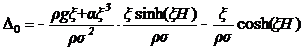
Далее находим ![]()
![]()
![]()
![]() :
:
![]() ,
, ![]() (5)
(5)
Формулы (3), (4), (5) дают решение поставленной задачи в трансформантах Фурье и Лапласа.
Проведем исследование свободной поверхности. Имеем:
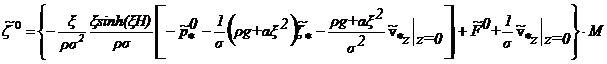
(6)
![]()
Отметим, что форма свободной поверхности зависит от всех возмущающих факторов: от внешнего давления, от возмущений дна, от начальных условий.
При этом каждый возмущающий фактор входит независимо один от другого в силу линейности задачи.
Применив теоремы о свертках для преобразования Лапласа
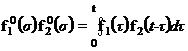
и для преобразования Фурье
![]() ,
,
мы получим решение задачи в интегральной форме. Для дальнейшего анализа формы свободной поверхности, надо задавать конкретные функции ![]()
![]() ,
,![]() ,
,![]() .
.
3. Управление амплитудой волн. Учитывая, что каждый возмущающий фактор можно изучать отдельно, положим ![]() .
.![]() Подберем теперь внешнее давление
Подберем теперь внешнее давление![]() так, чтобы его действие гасило волны, вызванные возмущениями дна. Имеем:
так, чтобы его действие гасило волны, вызванные возмущениями дна. Имеем:
![]() (7)
(7)
Приравняв числитель к нулю, находим:
![]()
Отсюда:
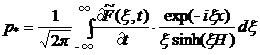 (8)
(8)
Вычисляя для конкретно заданной подвижки дна её трансформанту Фурье, находим, какое надо приложить внешнее напряжение к свободной поверхности водоема, чтобы на ней не возникали волны, вызванные движением дна.
4. Примеры. Пусть:
![]()
Здесь ![]() - любая функция от времени, которая описывает временную динамику деформации дна бассейна. Тогда:
- любая функция от времени, которая описывает временную динамику деформации дна бассейна. Тогда:
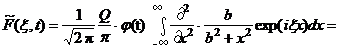
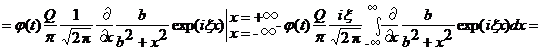
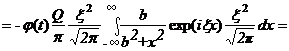
![]()
Такой выбор примера обусловлен тем, что в интеграле (8) в знаменатели стоит ноль второго порядка и его надо погасить для сходимости интеграла.
Теперь,![]() имеет вид:
имеет вид:
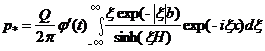 (9)
(9)
Последний интеграл табличный [3], (3.552)
![]()
Здесь![]() - дзета, функция Римана [3]:
- дзета, функция Римана [3]:
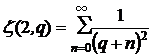 ,
, ![]()
Можно вычислить интеграл (9) и разложением подынтегральной функции на простейшие дроби:

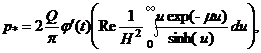
![]()
Или:
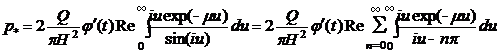
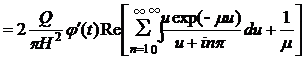
Последний интеграл табличный [3] (3.552). Имеем:

Воспользовались представлением [3] (8.215)
![]()

![]()
![]()
Окончательно выводим:
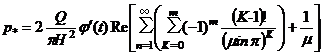
Конечно, в точно таком виде реализовать внешнее давление на поверхность водоема затруднительно. Но можно ограничиться несколькими членами построенных асимптотик. Безусловно, такие поверхностные воздействия не погасят полностью деформацию свободной поверхности жидкости. В асимптотическом плане соответствующие малые их значения могут быть рассчитаны исходя из полученных соотношений.
Литература
1 Кочин Н. Е., Кибель И. А., Розе И. В. Теоретическая гидродинамика, ч.1.// М.,физматгиз, 1963 г., 584 стр.
2 . К. Дж. Трантер. Интегральные преобразования в математической физике.// Государственное издательство технико-теоретической литературы. Москва 1956 г. 204 стр.
3 . И. С. Градштейн, и И. М. Рыжик. Таблицы интегралов, сумм, рядов и произведений// М., физматиз, 1962 г, 1100стр.