Численное решение нелинейной задачи устойчивости цилиндрических изотропных оболочек на основе динамического критерия
Аннотация
В рамках нелинейной потери устойчивости рассмотрена задача определения критического давления, распределенного по торцу цилиндрической оболочки. Критерием потери устойчивости является появление положительных ускорений, направленных по нормали к срединной поверхности оболочки. Численное решение осуществлено в системе MathCAD. Дан его сравнительный анализ с известным решением по формуле Папковича.
Ключевые слова: цилиндрическая оболочка, нелинейная устойчивость, численное решение, система MathCAD.Ключевые слова:
Уравнения, определяющие устойчивость цилиндрических изотропных оболочек относятся к классу «жёстких» нелинейных дифференциальных уравнений. Метод Рунге - Кутта - Фальберга и ему подобные требует много времени на составление программы численного решения, её отладку и само решение уравнений.
Самый простой способ их численного интегрирования предлагается системами руководства для решения инженерных задач Mathcad. Дифференциальные уравнения в них заменены уравнениями в конечных разностях и представлены в матричном виде.
Найдём критическое напряжение цилиндрической оболочки, сжатой силой q, равномерно распределённой по торцам оболочки (рис. 1).
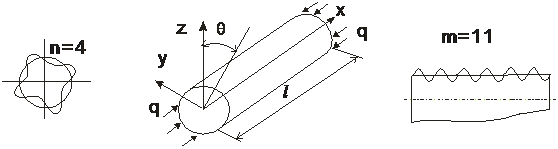
а б в
Рис.1
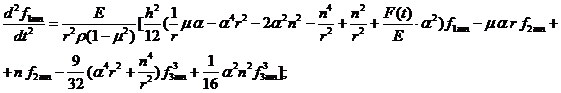
(1)
Уравнения (1) введением новых переменных, 
,
приводятся к нормальному виду задачи Коши и решаются численными методами.
В первом уравнении (1) заменим 
погонным значением силы q и будем считать, что она линейно изменяется во времени, а её наибольшее значение запишем через критическое напряжение 
, полученное по линейной теории устойчивости.
При таком представлении силы q критическое напряжение будет долей напряжения, найденного по линейной теории устойчивости.
Теперь уравнение (1) примет вид
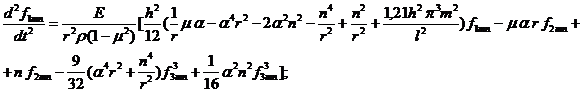
(2)
Для решения на ЭВМ оно приводятся к нормальному виду уравнений задачи Коши введением новых переменных
(3)
и уравнения (2) становятся уравнениями первого порядка.
Программы Mathcаdдлярешения систем этих уравнений очень просты, возможно и символьное, и численное решение задач.
Обозначим в (2) множители при квадратных скобках Ак , множители при амплитудах перемещений Вк , тогда (2 и 3) предстанут в виде
(4)
.
.
Программа решения «жёстких» дифференциальных уравнений для определения критической силы дана после представления в матричном виде.
Амплитуды перемещений точек fkи их производные
в начальных условиях обозначим
x1=f1, x2= f2, x3=f3 , x4=
,..x6=
,
а в решении задачи
t=z1, f1=z2, f2=z3, f3=z4; 
.
В этих обозначениях получится такая программа решения :
ORIGIN=1
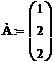
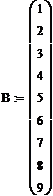
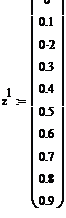
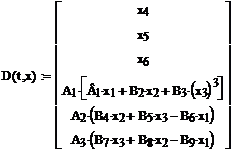. (5)
D(t, x) – матрица первых и вторых производных амплитуд перемещений, в ней А,- коэффициенты при первых производных,
,
,
;
,
Bk– коэффициенты при перемещениях,
x и z1- пределы интегрирования уравнений.
Последовательность вычисления амплитуд перемещений fi их производных 
c помощью операторов программирования Mathcad обычная – сверху вниз, справа налево.
Решение начинается с набора некоторой функции, например,
z= rkfixed (x, 0, 1, D, 100),
в которой начальное 0 и конечное 1 значения амплитуды прогиба, 100 – максимальное число шагов интегрирования уравнений.
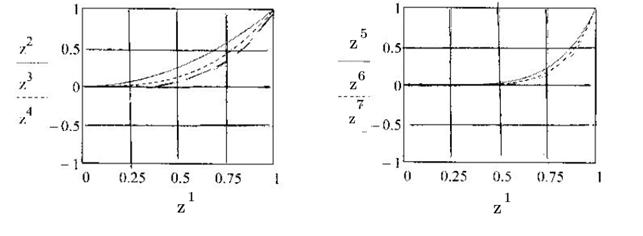
Решение выдаётся в виде графиков (рис.2).
Критическое время 
(рис.3б), время, до которого оболочка только сжимается по образующим её срединной поверхности, и докритическое состояние её безынерционно: ускорение по опасной гармонике амплитуды перемещений
Потеря устойчивости, динамический процесс, начинается с появления сил инерции (рис 3б), когда ускорение движения точки по нормали к срединной поверхности z5> 0.
При символьном решении уравнений Bkв матрице D (t, x) даны при числах волн т=п= 1.
Для численного решения уравнений элементы матрицы D (t,x)
B1=B1 (r, l, h, m, n, t), Bi=Bi (r, l , m, n ), i= 1, 2, 3,
коэффициенты при амплитудах перемещений fi=х1, f2=x2, f3=x3 , представляются векторами или функциями числа полуволн m=1, 2, 3, 4, 5, 6,7, 8 и числа волн n =2,3, 4, 5, 6,7, 8 , которые потом перебираются при каждом значении t < 1.
а б
Рис. 2
Решение может быть представлено и графиками, и таблицами.
Критическое время оболочки, как показано на рис. 2 соответствует z1= t=0.6, до которого оболочка только сжимается вдоль образующих её срединной поверхности.
Найденное таким решением уравнений устойчивости безразмерное критическое напряжение дюралюминиевой оболочки диаметром 0,5 м. длиной 2м. и толщиной 2мм. (r/h =250) соответствует математическому ожиданию безразмерного параметра критического напряжения 
=0,375 результатов известных экспериментов по рис.3.
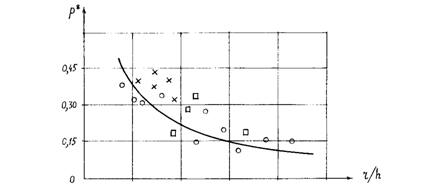
Рис.3
Критическое давление газа (жидкости), действующего на внешнюю поверхность цилиндрической оболочки, так же можно найти решением уравнений (1).
Если это давление одинаково по всей поверхности , в первом уравнении (1) оно представляется в виде 
.
Критическое время той же цилиндрической оболочки tkp = z1=0,5 (рис.2), соответствующее ему критическое давление составляет половину критического давления, найденного по формуле Папковича.
Заметим, кстати, что при практических расчётах найденное критическое давление для оболочек с r/h= 1000 по формуле Папковича умножают на 
= 0,5. Проекции вектора перемещений и вектора скоростей, когда при численном решении применяется функция z= rkfixed (x, 0, 1, D, 100), точны только в конечной точке.
По перемещениям точек оболочки определяются деформации,
,
,
,
затем напряжения по обобщённому закону Гука
,
,
.
По ним находят эквивалентное напряжение.