Априорная оценка термодинамических функций образования силикатных минералов и их кристаллогидратов

Аннотация

В.Т. Мальцев, Н.В. Мальцев

Процессы, связанные с получением различного назначения силикатных материалов всегда сопровождается энергетическим обменом между взаимодействующими фазами. Их термодинамический анализ не всегда возможен ввиду отсутствия соответствующего справочного материала.
В работе предлагается априорная оценка термодинамических функций образования силикатных, а так же других оксидных минералов,  и их кристаллогидратов.
Ключевые слова: силикаты, термодинамика, функции, образование, теплоемкость.

Ключевые слова:

05.23.05 - Строительные материалы и изделия

Физико-химический анализ многих процессов, связанных с получением силикатных материалов, в том числе керамик различного назначения, тепловые расчеты теплообменных агрегатов, включая обжиговые печи, в той или иной степени связаны с количественной оценкой энергетических эффектов протекающих в них химических реакций. Такая оценка возможна, если известны термодинамические функции образования (∆Н, ∆С, S) соединений, участвующих в них, и нх зависимости от температуры.
Согласно известному закону Гесса, изменение обобщенной термодинамической функции Z_xр при протекании химической реакции при фиксированной температуре равно разности термодинамических функций образования продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов, стоящих в уравнении реакции
Так, например, для реакции
aA+bB=сС+dD+ Z_xр,
(где А, В — исходные вещества С и D — продукты реакции; а, b, с, d — стехиометрические коэффициенты)
Z_xр = (с Z_С+ dZ_D) — (аZ_А + bZ_B).

 Зависимости Z_xр = f(T) определяются известными уравнениями

, где ∆C_p— разность сумм теплоемкостей продуктов реакции и исходных веществ с учетом коэффициентов, стоящих в уравнении реакции.
Теплоемкость твердых индивидуальных веществ в зависимости от температуры обычно описывается степенными рядами
C_p =a + bT +C/T² или
Cp =a + bT +C/T²+dT³
Справочные данные [1, 2, 3, 4] по термодинамическим функциям образования и температурной зависимости Ср = f(T) носят ограниченный характер и обычно относятся к простым по составу минералам. В связи с этим значительное развитие получили различные методы сравнительного расчета [3, 5, 6] термодинамических функций одних веществ и реакций по экспериментальным данным, относящихся к другим Веществам и реакциям.
Практически все они основаны на закономерной аналогии термодинамических свойств соединений, близких по химическому составу и строению, или связаны между собой с определенным положением в периодической системе, входящих в них элементов.
Однако в химии силикатов, большое количество соединений, включая и кристаллогидраты, не имеет или ограниченно имеет аналоги по составу и строению. Из-за отсутствия достаточного количества справочного материала фактически невозможно оценить их термодинамические функции образования по известным аддитивным схемам и, как следствие, провести соответствующие термодинамические расчеты по химическим реакциям с их участием.
Следовательно, изыскание априорных методов расчета термодинамических функций образования таких соединений является довольно актуальной задачей.
Рассмотрим последовательно термодинамику химического взаимодействия в двойных, тройных оксидных системах при стандартных условиях и в зависимости от температуры.
Изменение стандартных термодинамических функций образования (Z⁰(1-x)A·xB) двойных и более сложных соединений можно рассматривать как состоящее из двух составляющих: 1 — «аддитивной», являющейся алгебраической суммой термодинамических свойств компонентов и 2 — «избыточной», определяющей энергетику взаимодействия оксидов с образованием рассматриваемого соединения. Для соединения (1-x)A·xB образующегося по реакции 
(1-х)А+хВ=(1-х)A∙xB+Z⁰x.p., где А и В — исходные оксиды; х — мольная доля одного из них,
Z⁰_(1-x)A·_xB=(i-x)Z⁰_A+xZ_B+Z_x.p.
Учитывая, что термодинамические свойства оксидов хорошо изучены и широко представлены в справочной литературе, задачу сводим к нахождению Z⁰_x._p, т.е. к нахождению термодинамических функций образования соединений из компонентов в частности, оксидов.
Как было отмечено [7] энергетическую структуру сложного минерала можно интерпретировать как кристаллическую решетку более простого минерала с конденсацией в ней одного из оксидов. Взаимная конденсация основных и кислых оксидов, как имеющих положительное сродство (ΔG_x.p.<0), всегда связана с процессом деполимеризации и перераспределением химических связей. Поскольку взаимное химическое средство имеется при любых соотношениях исходных компонентов, следует ожидать, что в первом приближении Z⁰_x.p.должна быть непрерывной функцией состава, при выражении последнего в мольных долях. Следует признать, что в двойных, тройных системах с химическим взаимодействием возможно образование бесконечного числа соединений, из которых в силу геометрических, структурных и иных факторов стабильными являются только дискретные.
Максимальное химическое сродство можно наблюдать при полном взаимном насыщении химических связей, т.е. в соединениях островного характера, построенных из ионов: ВО₃^-3, Si0₄^-4, РО₄^-3, Cr0₄^-2и т.д., связанных между собой ионами металлов, например, в орто — силикатах, - фосфатах. Анализ справочных данных (табл. 1) в целом подтверждает вышесказанное, а также и то, что основной вклад значения ∆Н­⁰₂₉₈и ΔG⁰₂₉₈вносит химическое средство, а не структурный факт
Отличие этих функций для различных кристаллических модификаций одних и
же соединений составляет менее 3%.
Таблица 1

∆Н­⁰₂₉₈ -, ΔG⁰₂₉₈образование некоторых двойных соединений из оксидов

При выражении составов соединений в мольных долях изменение ∆S⁰_{298 x.p.}
при реакциях их образования из оксидов, включая процессы гидратации, мало зависит от их соотношения (табл. 2), по крайней мере, в области умеренных температурах следовательно, ∆Н_m, ΔG_m— образования соединений в зависимости от мольных долей их компонентов можно описать уравнениями, отличающимися значением только одного из слагаемых, равного Т ΔS_m практически мало зависящего от состава, т.е. уравнением одного вида.
∆S­0298 - образование соединений из оксидов

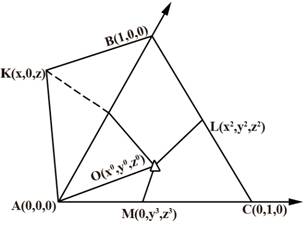
В двойной системе А — В (см. рисунок) с соединением К — соответствующей
составу (1 — х)А∙хВ и характеризующейся максимальным значением химического
средства компонентов (Z₁), изменение z = f(х) можно описать уравнениями двух

Таким образом, для расчета ∆Н⁰₂₉₈ -, ΔG⁰₂₉₈— образования соединений с любым соотношением компонентов требуются данные по одному любого состава.

Из сравнительного анализа (табл. 3) справочных и расчетных данных по термодинамическим функциям образования соединений из простых веществ можно сделать вывод о правомочности такого подхода. Расхождения составляют менее 1%, что значительно меньше, чем экспериментальные данные различных авторов по одним и тем же соединениям.
В приложении в тройной системе АВС (см. рисунок), где К, L, М соответствуют составам двойных соединений с максимальными взаимно насыщенными связями между компонентами изменение Z — образования тройных соединений можно задать уравнениями шести плоскостей, пересекающихся в точке O(x₀, у₀, z₀). Координаты точки О в мольных долях вероятнее всего будут определяться численными значениями Z — образований двойных соединений:

где ∑Z_i — сумма Z_i — образования двойных соединений с максимальным взаимным насьпцением компонентами химических связей.
Таблица 3
Справочные и расчетные данные по стандартным термодинамическим функциям образования некоторых соединений

Уравнения плоскостей можно записать в следующем виде:

Таким образом, для расчета ∆Н⁰₂₉₈ - или ΔG⁰₂₉₈— образований тройных соединений из компонентов любого состава требуются знания этих функций одного из них.
В табл. 4 проведено сопоставление справочных и расчетных данных ∆Н⁰₂₉₈ образования некоторых силикатов, алюминатов, их кристаллогидратов из простых веществ. Как следует из табличных данных, относительное расхождение в редких случаях составляет более 1%.
Реальные процессы протекают при температурах, как правило, отличных от стандартной. Расчет термодинамических функций при этих условиях предполагает знание Ср = f(т) всех участников реакций. Справочные данные по таким зависимостям так же носят ограниченный характер.
Таблица 4

Поэтому необходима априорная оценка этих величин.
Известно, что зависимость молярной теплоемкости соединения от температуры обычно описывается степенными рядами С_p = а + bТ+сТ^-2или Ср = а + bТ+сT².
Основной вклад в значения теплоемкостей минералов, вероятно, вносят прежде всего валентные и деформационные колебания атомов в анионной подрешетке, лежащие в инфракрасной области, и колебания катионов, лежащие в более длинноволновой части спектра. ИК — спектры практически всех силикатов алюмосиликатов, боратов, фосфатов их кристаллогидратов характеризуются одинаковым набором фундаментальных полос поглощения полиэдров — [ЭО₄],[ ЭО₃] с некоторым расщеплением, зависящим от соотношения основного и кислого оксидов в соединениях [10].
Можно полагать, что теплоемкость минералов и их кристаллогидратов, в первом приближении, будет аддитивной функцией теплоемкостей и мольных долей образующих их оксидов. Это означает, что при умеренных температурах значения констант а, b, с  в Сp=f(T)соединений с любым соотношением компонентов также будут аддитивными функциями мольных долей оксидов. Сопоставление справочных и расчетных зна-чений теплоемкостей (табл. 5) говорит о правомочности такого подхода. Расхождение, например, для силикатов натрия в температурном интервале 298-800К составляет не более 2Дж/град моль.
Таблица 5
Справочные [2] и расчетные значения Ср = 1(т) силикатов натрия

Представленные методы позволяют априори на основе имеющегося справочого материала оценивать термодинамические функции образования многих сложных по составу соединений и проводить термодинамический анализ процессов с их участием.

Литература
1. Карапетьянц МХ, Карапетьянц МЛ.Основные термодинамические константы неорганических и органических веществ. — М.: Химия, 1968. - 470с.
2. Гороновский И.Т.и др. Краткий справочник по химии. — Киев: Наукова думка, 1974. - 984с.
3. Киреев В.А.Методы практических расчетов в термодинамике химических реакций. — М.: Химия, 975. - 535с.
4. Бабушкин В.И.и др. Термодинамика силикатов. — М.: Госстройиздат, 1962.26бс.
5. Кутолин С.А. Аддитивная схема расчета стандартных теплот образования минералов класса силикатов //Изв. Сибир. отд. АН СССР. Химия, 1965. - С. 141-143.
6. Карапетьянц М.Х .Методы сравнительного расчета физико-химических свойств. — М.: Наука, 1965. — 403 с.
7. Кутолин С.А., Смирнова Е.Г.Физико-химический смысл инкрементов в методах сравнительного расчета и их применения к анализу свойств соединений редкоземельных элементов // Физическая химия. — 1977. — Т. 51. — №10. — С. 2571-2575.
8. Куколев ГВ.Химия кремния и физическая химия силикатов. -Мл Высш. школа, 1966. — 462с.
9. Николаев В.А., Доливо-Добровольский В.В.Основы теории процессов магнетизма и метафоризма. — М.: Наука, 1961. -209с.
10. Власов А.Г., Флоринская В.А.Инфракрасные спектры неорганических стекол и кристаллов. — Лл Химия, 1972. -303с.