Модели кооперации в системе социального партнерства

Аннотация

Л.В. Тарасенко, Г.А. Угольницкий, В.К. Дьяченко

Дата поступления статьи: 13.03.2013

Предлагается формализация социально-партнерских отношений в системе дополнительного профессионального образования с помощью математического аппарата теории кооперативных игр. Построена игра голосования трех лиц, проведен сравнительный анализ различных принципов оптимальности для характерных значений числа голосов игроков

Ключевые слова: социальное партнерство, дополнительное профессиональное образование, игры голосования, С-ядро, НМ-решение, вектор Шепли

05.13.18 - Математическое моделирование, численные методы и комплексы программ

22.00.04 - Социальная структура, социальные институты и процессы

Неразработанность механизмов социального партнерства, сохраняющегося разрыва связей с работодателями, социальными партнерами порождает проблему разработки концептуальных основ формирования региональной социокультурной модели социального партнерства в системе дополнительного профессионального образования (ДПО) [1].В рамках общей теории социального управления Г.П. Зинченко рассматривает понятие «социальное партнерство» как форму взаимодействия многообразных субъектов социума (государственных институтов, корпораций, некоммерческих организаций, социальных групп и др.), позволяющую им свободно выражать свои интересы и находить цивилизованные способы их реализации [2]. Данное определение принято авторами в качестве рабочего понятия при изучении механизмов социального взаимодействия в дополнительном профессиональном образовании, как частном случае его применения. Все совокупные субъекты социального партнерства в системе ДПО могут быть разделены на две группы: 1 – субъекты, вступающие во взаимодействия между собой на мезосоциальномуровне (учреждения ДПО, органы государственной власти, работодатели); 2 – на  микросоциальном (преподавательский состав учреждений ДПО и контингент обучающихся). Таким образом, «партнерство» - это взаимодействие участников образовательного процесса, с одной стороны. С другой, социальное партнерство субъектов в системе ДПО – это отношения между коллективными субъектами, заинтересованными на определенном этапе взаимодействия в эффективности ДПО. К тому же партнерство является культурным явлением, потому что в нем отражены традиции конкретного этапа культурного развития общества. Сущность социального партнерства заключается в равноправном взаимодействии социальных (административно-правовых, гражданских, культурных и образовательных учреждений), производственных субъектов и бизнес-структур, направленном на целесообразное выполнение профессионально – образовательной миссии образовательным учреждением системы ДПО [3].
Из вышеизложенного вытекает целесообразность описания процессов социального партнерства вообще и в системе ДПО в частности с помощью математического аппарата теории кооперативных игр, позволяющего моделировать образование коалиций субъектов и их взаимодействие [4,5,6]. Методика моделирования социальных процессов описана авторами в работах [7,8,9]
Удобной кооперативно-игровой моделью служат так называемые игры голосования [10]. Игра голосования с характеристической функцией определяется формулой

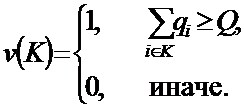(1)

Здесь величина  интерпретируется как число голосов, которыми располагает игрок . Таким образом, коалиция побеждает , если набирает не менее нужного числа голосов , и проигрывает в противном случае. Удобно задавать игру голосования строкой .
В модели социального партнерства в системе дополнительного профессионального образования (ДПО) игроками являются работодатель (i=1), ВУЗ (i=2) и студент (i=3). В общем случае можно интерпретировать qi как комплексный ресурс игрока i, а Q - пороговое значение ресурса, при котором социальное партнерство является эффективным. В качестве примера будем придерживаться трактовки, согласно которой Q – стоимость реализации программы ДПО, q_i – сумма, которую игрок i готов инвестировать в проект. Программа может быть выполнена, если участники совместно инвестируют в ее реализацию необходимую сумму Q.
Рассмотрим игру голосования вида (1). В предложенной трактовке выигрывающими являются те и только те коалиции, которые располагают необходимыми средствами для реализации программы ДПО, а решение игры показывает принцип распределения полученных доходов.
Положим для определенности q₁ < q₂ < q₃ , то есть упорядочим участников по возрастанию их готовности инвестировать в программу. Будем считать также, что  q₁ + q₂ > q₃ (в противном случае инвестиционный ресурс третьего игрока превосходит суммарный ресурс двух остальных, и объединение становится  существенно неравноправным). Очевидно, что представляет интерес рассмотрение программ, стоимость реализации которых находится в диапазоне  Действительно, если Q ≤ q₃ , то третий игрок может реализовать программу самостоятельно, и необходимости в объединении не возникает. Если же Q > q₁ + q₂ + q₃ , то даже объединения ресурсов всех игроков все равно недостаточно для реализации программы. Проведем анализ всех возможных случаев соотношения ресурсов игроков и стоимости программы при сделанных предположениях.
1. q₃ < Q ≤ q₁ + q₂. В этом случае все одноэлементные коалиции проигрывающие, а все двухэлементные и максимальная коалиция – выигрывающие. Игра симметрична, С-ядро в ней отсутствует. Вектор Шепли имеет вид то есть в этом распределении все игроки получают одинаковую долю дохода от реализации программы. Имеется устойчивое множество , которое представляет собой так называемое дискриминирующее решение. Это означает, что те два игрока, которые первыми объединятся и создадут выигрывающую коалицию, исключают третьего игрока из распределения дохода, деля его поровну между собой.
2. q₁ + q₂ < Q ≤ q₁ + q₃ . Здесь участия третьего игрока необходимо и достаточно, чтобы неодноэлементная коалиция была выигрывающей, поэтому С(v) = {(0,0,1)},  Хотя третий игрок не является здесь в полном смысле слова диктатором, но его роль в инвестировании существенно выше, чем у двух других игроков, поэтому в С-ядре он забирает весь доход полностью, а в более демократичном векторе Шепли – две трети дохода.
3. q₁ + q₃ < Q ≤ q₂ + q₃ . Здесь в системе для определения С-ядра ненулевую правую часть имеют соотношения
 поэтому . Из соображений симметрии и неучастия первого игрока получаем вектор Шепли в виде  Таким образом, здесь основную роль в инвестировании играют более сильные второй и третий игроки, которые и делят между собой инвестиционный доход, исключая первого игрока из распределения.
4. q₂ + q₃ < Q ≤ q₁+ q₂ + q₃ . Здесь единственной выигрывающей коалицией является максимальная (то есть для реализации программы требуется обязательное объединение усилий всех игроков, которые в этом случае делят инвестиционный доход поровну).

Литература:
1.Тарасенко, Л.В. Моделирование социального партнерства в системе дополнительного профессионального образования // Общество: социология, психология, педагогика. 2011. - №4.
2.Михеев, В.А. Основы социального партнерства: теория и политика [Текст] / В.А. Михеев. – М., 2001.
3.Зинченко, Г.П., Рогов, И.И. Социальное партнерство: [Текст]: Учебник / Г.П. Зинченко, И.И. Рогов. – М.: Издательско-торговая корпорация «Дашков и К°»; Академцентр, 2009. – 224 с.
4.Петросян, Л.А. Теория игр [Текст] / Л.А.Петросян, Н.А.Зенкевич, Е.В.Шевкопляс. - СПб.: БХВ-Петербург, 2012. - 432 с.
5.Petrosjan, L.A., Zenkevich, N.A. Game theory. - Singapore, London: World Scientific Publishers, 1996.
6.Petrosjan, L.A., Zaccour G. Time-consistent Shapley value allocation of pollution lost reduction [Text] // Journal of Economic Dynamics and Control. - 2003. - Vol.27. - P.381-398.
7.Розин М.Д., Сущий С.Я., Угольницкий Г.А., Антоненко А.В. Дескриптивный подход к моделированию коррупции как фактора социальной конфликтности // Инженерный вестник Дона. 2011. №3.[Электронный журнал]. - № гос.регистрации 0421100096. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2011/561.
8.Сущий С.Я., Угольницкий Г.А., Дьяченко В.К., Сивогривов А.А. Математическая модель кадровой пирамиды бандподполья на Северном Кавказе // Инженерный вестник Дона. 2012. №2. [Электронный журнал]. - № гос.регистрации 0421100096. –http://ivdon.ru/magazine/archive/n2y2012/845.
9.Сущий С.Я., Угольницкий Г.А., Дьяченко В.К., Сивогривов А.А. Сценарное моделирование борьбы с экстремизмом на Северном Кавказе // Инженерный вестник Дона. 2012. №2. [Электронный журнал]. - № гос.регистрации 0421100096. –http://ivdon.ru/magazine/archive/n2y2012/847.
10.Мазалов В.В. Математическая теория игр и ее приложения. - СПб.: Лань, 2010. - 448 с.