Концепция организации обработки информации в системах диагностики и распознавания

Аннотация

М.П. Берестень, А.Ю. Зенов

Дата поступления статьи: 12.03.2013

В статье рассмотрены проблемы, возникающие при построении систем диагностики и распознавания, приведены методы позволяющие выявить отклонения в функционировании различных объектов.

Ключевые слова: диагностика, разложение на эмпирические моды, экстремальная фильтрация, время-частотное распределение

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Проектирование любой системы диагностики (распознавания) начинается с создания модели диагностируемого (распознаваемого) объекта. Такую модель можно, например, построить на основе априорной информации об объекте или по экспериментальным данным, регистрируемым датчиками – вибрациям, акустическим шумам, переменным давлениям и т.д.
Невозможно построить универсальную модель различных объектов, но можно построить универсальную модель быстропеременных процессов, которые сопровождают их работу и отражают свойства. Часто быстропеременный процесс представляет собой комбинацию узкополосных составляющих аддитивно смешанных с широкополосным шумом.
Свойства процесса претерпевают изменения с течением времени или под действием влияющих факторов. Это проявляется в изменении амплитуд и частот узкополосных составляющих, уровня широкополосного шума, появление гармоник или субгармоник основной частоты возбуждения и др. При таких условиях задача выявления отклонений в функционировании объектов может быть сведена к обнаружению моментов изменения частотных свойств случайного процесса.
Такая модель (сумма узкополосных составляющих) объясняет, почему классические системы диагностики строятся на парадигме спектрального анализа – в спектре, как правило, выделяются выраженные резонансы (моды), по которым можно судить об изменении в объекте.
Известно, что спектральный анализ подразумевает разложение по ортогональному тригонометрическому базису. Трудоемкость такого анализа достаточно высока, а так как нас интересует изменение свойств во времени, то стоит говорить о спектрально – временном анализе, т.е. о время - частотном распределении, вычисление которого еще более трудоемко.
Рассмотрим методы цифровой обработки сигналов, наиболее согласованные с предложенной моделью сигнала.
В настоящее время широко применяется преобразование Гильберта – Хуанга (HHT), которое включает в себя две части: разложение по эмпирическим модам (EMD) и спектральный анализ Гильберта (HSA), при котором определяют мгновенную частоту как функцию времени, позволяющую получить отчетливую идентификацию внутренней структуры процесса. Итоговым результатом является трехмерное представление “амплитуда (мощность) – частота - время”. На первом этапе (EMD - разложение) выделяются именно те составляющие, которые характеризуют модель в текущий момент времени [1, 2].
У этого преобразования имеется аналог – экстремальная фильтрация, позволяющая разложить сигнал на знакопеременные составляющие. В результате фильтрации выделяются субполосные составляющие (моды), каждая из которых характеризуется частотой и амплитудой (мощностью). Основные принципы экспресс-анализа изложены в работах [3-7]. На рис. 1 представлено разложение на знакопеременные составляющие с помощью EMD - разложения (сплошная линия) и экстремальной фильтрации (точки на графиках).

Рис. 1. – Разложение сигнала на знакопеременные составляющие

Знакопеременную составляющую можно выделить путем центрирования относительно скользящего среднего. Наиболее простым является метод, в котором используются лишь экстремальные значения x_эi, где i=1,2,...,m. Сглаживание производится оператором вида:
, (1)
который соответствует пропусканию данных через цифровой фильтр нижних частот. Первая, высокочастотная, составляющая определяется из соотношения:
.
Составляющая может быть выделена непосредственно из экстремумов фильтром высоких частот:
   (2)
Далее преобразования вида (1), (2) повторяются над составляющей . Так как расстояние между экстремумами на каждом шаге увеличивается, то фильтры (2) – полосовые по отношению к диапазону , определяемому шагом дискретизации .
Каждую из знакопеременных составляющих можно связать с полосой частот, что дает возможность оценить частотные (в том числе и время-частотные) характеристики сигнала.
Параметры разложения частота и амплитуда (мощность) каждой составляющей сигнала характеризуют модель объекта в текущий момент:

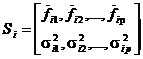
где  – значения центральной частоты j-й компоненты на i-м участке (при анализе в скользящем окне);  – значения мощности j-й компоненты на i-м участке; р– количество компонент.
Зависимость  характеризует спектр мощности в текущий момент времени, а  - время частотное распределение.
Распределение по шкале моментов появления экстремумов в разных составляющих имеет важное свойство: самая высокочастотная составляющая содержит экстремумы, абсциссы которых определяют положение экстремумов и всех низкочастотных составляющих. Это свойство может быть использовано для дополнительного сжатия данных без потерь информации об абсциссах экстремумов.
При оценивании характеристики не используется разложение по ортогональному базису. Кроме того, коэффициенты фильтра допускают использование вместо умножения сдвиг вправо на 1 или 2 разряда, соответственно, что более экономично с точки зрения вычислений.
Для восстановления составляющих могут быть использованы различные способы аппроксимации функций, но важно, чтобы при этом учитывались особенности выделенных составляющих, а именно тот факт, что они представляют собой последовательность знакопеременных экстремумов. В частности, аппроксимация может быть выполнена полупериодами косинусоиды соответствующей частоты, соединяющими соседние экстремумы или же колокольными составляющими вида , амплитудные параметры которых определяются экстремумами, а временные – расстояниями между соседними экстремумами.
Хотя в этом методе выделяются субполосные составляющие (то есть не разделяются близкие гармоники), он является достаточно эффективным, простым, нетрудоемким способом спектрального оценивания, а параметры выделенных знакопеременных составляющих позволяют сформировать диагностические признаки. Количество знакопеременных составляющих p, их параметры – амплитуды (или среднеквадратические отклонения) A_i, частоты , i= 1... p могут быть положены в основу формирования диагностических признаков. На рис. 2 представлен спектр полигармонического сигнала и его экспресс-оценка.
Отметим, что метод экстремальной фильтрации удовлетворяет противоречивым требованиям к методам цифровой обработки в системах диагностики: вычислительная трудоемкость анализа не должна превышать заданного времени; достоверность анализа должна быть не менее заданной.

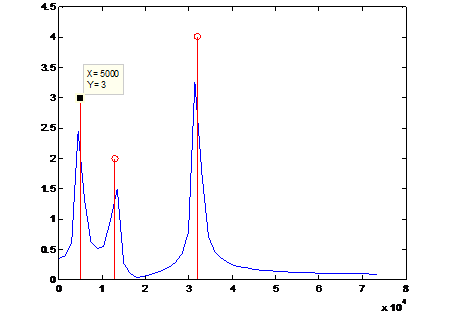
Рис. 2. – Спектр Фурье и экспресс-спектр

На рис. 3 приведен пример анализа сейсмического сигнала [8-10]. На рисунке видно изменение параметров при переходе от сейсмошума при вторжении в зону ответственности. Два нижних графика на этом рисунке в совокупности образуют время-частотное распределение сигнала.
Вопросы обработки и принятия решения в технических системах остаются актуальными и многие авторы уделяют им внимание [10, 11].
Авторы в качестве вторичного признака предлагают использовать моменты спектра мощности, характеризующие его форму. Центральный момент порядка n спектра мощности определяется как
,   (3)
где  – центральная частота процесса, которая может быть определена как отношение начальных моментов спектра – первого и нулевого порядков.

 Для экспресс-оценки спектра центральная частота определяется соотношением:
,
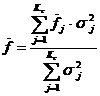где K_c – количество узкополосных компонент сигнала.
Тогда, переходя к форме представления спектра , перепишем (3) в виде:
.
По аналогии с моментами распределения случайной величины второй центральный момент µ₂ характеризует компактность спектра (аналог – дисперсия), третий центральный момент µ₃ – его симметрию (аналог – коэффициент асимметрии) и т.д.
Решающее правило имеет следующий вид:
,
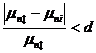где µ_nб – центральный момент порядка n спектра мощности на базовом участке; µ_ni – центральный момент порядка n спектра мощности на i-м участке; d – допуск.
Считается, что если относительное изменение величины момента спектра мощности на текущем участке больше допуска, то имело место изменение свойств сигнала.

Выводы

1. Предложена концепция единства модели сигналов в сейсмических, вибрационных системах, описываемой суммой узкополосных составляющих аддитивно смешанных с шумом и способов цифровой обработки, выделяющих узкополосные составляющие из сигнала: разложения на эмпирические моды и разложение на знакопеременные составляющие на основе экстремальной фильтрации. Параметры выделенных составляющих характеризуют объект в текущий момент времени. По изменению этих параметров можно судить о вторжении и его типе в режиме реального времени.
2. Обосновано применение для анализа сейсмических и вибрационных сигналов экстремальной фильтрации как наименее трудоемкого метода, позволяющего интерпретировать результаты фильтрации как параметры модели, частотные и время-частотные характеристики.

Литература:

1. Flandrin, P. Empirical mode decomposition as filter bank / P. Flandrin, P. Gonçalves, G. Rilling // IEEE Sig. Proc. Lett. – 2004. – Vol. 11, №2. – P. 112-114.
2. Norden E. Huang, Samuel S. Shen Hilbert-Huang Transform and Its Applications // World Scientific Publishing Company – 2005.  − Vol.  5. − 324 p.–ISBN: 9812563768
3. Строганов, М.П., Обработка сигналов в системах диагностики: моногр. / М.П.Строганов, М.П.Берестень, Н.В Мясникова; под редакцией Е.П. Осадчего: Монография. - Пенза: Изд-во Пенз. гос. техн. ун-та, 1997.- 119 с.:32 ил., библиогр. 44 назв.
4.Мясникова, Н.В., Экспресс-анализ сигналов в технических системах: моногр. / Н.В. Мясникова, М.П.Берестень. – Пенза: Изд-во ПГУ, 2012.–152с.;72 ил., библиогр. 44 назв., 2012г.
5. Мясникова Н.В., Экстремальная фильтрация и ее приложения / Н.В. Мясникова, М.П. Берестень // Датчики и системы, №4, 2004. - С. 8-11.
6. Мясникова, Н.В., Теоретические основы экспресс-анализа / Н.В. Мясникова, М.П. Берестень // Известия высших учебных заведений. Поволжский регион. Технические науки. №6, 2006.- С.117-123.
7. Мясникова, Н.В., Берестень М.П., Дудкин В.А. Экспресс-анализ сейсмических сигналов/ Н.В Мясникова, М.П.Берестень, В.А. Дудкин // Известия Вузов. Поволжский регион. Технические науки, №4, 2007. – С. 144 – 151.
8. Мясникова, Н.В. Применение разложения по эмпирическим модам в задачах цифровой обработки сигналов/ Н.В. Мясникова, Л.А. Долгих, М.Г. Мясникова// Датчики и системы – №5, 2011, С. 8-10.
9. Зенов, А. Ю. Комплексный подход к обнаружению и классификации нарушителя на охраняемой территории / А. Ю. Зенов // Известия высших учебных заведений. Поволжский регион. Технические науки. – 2012. – № 2. – С. 23–32.
10. Зенов, А.Ю. Применение нейросетевых алгоритмов в системах охраны периметра /А. Ю. Зенов, Н. В. Мясникова / Известия ВУЗов. Технические науки. Поволжский регион. №3. С. 15–24.
11. Обработка диагностической информации при оценке технического состояния электроприводной арматуры АЭС. [Электронный ресурс]: Инженерный вестник Дона №3 2011 – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2011/502/ - Загл. с экрана. – Яз. рус.
12. Антонова А.С., Аксенов К.А. Многокритериальное принятие решений в условиях риска на основе интеграции мультиагентного, имитационного, эволюционного моделирования и численных методов [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (Часть 2). – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1466 (доступ свободный) - Загл. с экрана. – Яз. рус.