Математическая модель и оптимизация параметров работы пластинчатого рекуператора

Аннотация

И.В. Кряклина

Дата поступления статьи: 30.12.2013

Использование нетрадиционных и возобновляемых источников энергии имеет важное народнохозяйственное значение для энергосбережения. Пластинчатые рекуператоры применяются для повторного использования тепла отходящего воздуха в системе вентиляции зданий. Для повышения энергоэффективности и оптимизации параметров работы пластинчатого рекуператора разработана  его функциональная математическая модель. На основании математической модели определен критерий оптимизации и установлены оптимальные режимы функционирования рекуператора вентиляционного воздуха. В результате исследований установлено, что для повышения эффективности работы рекуператора необходим подогрев наружного воздуха перед входом  в рекуператор. Для решения этой задачи предлагается использовать грунтовой теплообменник.

Ключевые слова: математическая модель, пластинчатый рекуператор, нетрадиционные источники энергии, оптимизация, энергосбережение

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Важное народнохозяйственное значение для энергосбережения и повышения энергоэффективности имеет использование нетрадиционных и возобновляемых источников энергии (НВИЭ). Строительство энергоэффективного жилья с НВИЭ является актуальным для  России [1]. Поэтому необходимо интенсифицировать работы по внедрению для отопления, вентиляции и кондиционирования зданий  машин и устройств, которые могут уменьшить  энергопотребление при сохранении  комфортных условий [2, 3]. Рекуператоры как раз такие устройства, которые применяются для повторного использования тепла отходящего воздуха в системе вентиляции зданий.
Рекуператоры вентиляционного воздуха бывают различными по конструкции: пластинчатыми, роторными, камерными, рекуператорами с промежуточным теплоносителем, рекуператорами – тепловыми трубами      [4,5].  
Для повышения эффективности работы пластинчатого рекуператора вентиляционного воздуха необходимо использовать его максимальные возможности для возврата тепла отработанного воздуха при оптимальных режимах функционирования. 
Разрабатываем функциональную математическую модель процесса работы пластинчатого рекуператора в виде динамической системы, которая выполняет преобразование входных возмущающих  и управляющих воздействий в выходные переменные параметры [6]: 
Ф_i ( X, Y, Z, t ) = 0,
где   X = [x₁, x₂, x₃, …, x_n] t  - вектор входных параметров; Y = [y₁, y₂, y₃, …, y_n] t - вектор выходных параметров; Z = [z₁, z₂, z₃, …, z_n] t  - вектор управляющих параметров; t– координата времени.
Принимаем входными параметрами процесса возврата тепла в энергоэффективный дом параметры наружного и удаляемого воздуха, значения которых заранее известны и определяют режим работы пластинчатого рекуператора.  Выходными параметрами являются параметры приточного и вытяжного воздуха. Значения выходных параметров определяются режимом процесса работы пластинчатого рекуператора и управляющими параметрами. Управляющие параметры – это переменные характеристики процесса, на которые можно оказывать прямое воздействие в соответствии с требованиями, что позволяет управлять процессом возврата тепла в энергоэффективный дом.
Графическое изображение  функциональной математической модели пластинчатого рекуператора представлено на рисунке.

 
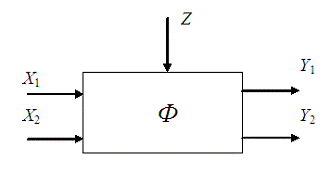
Схема функциональной  динамической математической модели  пластинчатого рекуператора

Обозначим векторы:
X₁ = {t_н; G_н; с_н; φ_н} – входной вектор параметров наружного воздуха.
t_н  - температура наружного воздуха, ºC;G_н – расход наружного воздуха, кг/с; с_н – теплоемкость наружного воздуха, Дж/(кг·К); φ_н – относительная влажность наружного воздуха, %.  
X₂ = {t_у;G_у; с_у; φ_у; q₁} – входной вектор параметров удаляемого воздуха.t_у, ºC – температура удаляемого воздуха; G_у – расход удаляемого воздуха, кг/с;  с_у – теплоемкость удаляемого воздуха, Дж/(кг·К); φ_у – относительная влажность удаляемого воздуха, %; q₁ – тепловой поток, передающийся удаляемым наружному воздуху, Вт.   
Y₁ = {G_п; с_п; φ_п; q₂} – выходной вектор приточного воздуха.
G_п – расход приточного воздуха, кг/с; с_п – теплоемкость приточного воздуха, Дж/(кг·К); φ_п – относительная влажность приточного воздуха, %; q₂ – тепловой поток, получаемый приточным воздухом, Вт.
Y₂ = {t_в;G_в; с_в; φ_в} – выходной вектор вытяжного воздуха.  t_в – температура вытяжного воздуха, ºC;G_в – расход вытяжного воздуха, кг/с; с_в – теплоемкость вытяжного воздуха, Дж/(кг·К); φ_в – относительная влажность вытяжного воздуха, %.
Z = {t_п; q₃; G_к} –  вектор переменных управляющих параметров;tн  - температура  приточного воздуха, ºC; q₃ – потери тепла рекуператором  в окружающую среду, Вт; G_к – расход конденсата, кг/с.
В соответствие с проведенными исследованиями имеем выражения для функциональной математической модели пластинчатого рекуператора вентиляционного воздуха:
Y₁= Ф₁ [X₁, X₂, Z] =  Ф₁ [t_н;G_н; с_н; φ_н;t_у;G_у; с_у; φ_у; q₁; q₃ ](1)                                                       
Y₂= Ф₂ [X₁, X₂, Z] = Ф₂ [t_н;G_н; с_н; φ_н;t_у;G_у; с_у; φ_у; q₁; q_{3 ]  (2)                    
На основании разработанной функциональной математической модели пластинчатого рекуператора вентиляционного воздуха переходим к расчету и оптимизации параметров пластинчатого рекуператора с определением целевой функции для нахождения критерия оптимизации.
Главная цель практического использования пластинчатого рекуператора – получение максимума тепла от удаляемого из помещения воздуха при имеющихся технических возможностях рекуператора и физических параметрах наружного и удаляемого воздуха [7, 8].
В соответствии с функциональной математической моделью функционирование пластинчатого рекуператора полностью характеризуется следующими информационными переменными:  tн;Gн; сн; φн;tу;Gу; су; φу; q1; q2; q3; tп .
Регламентированными переменными являются: tн;Gн; сн; φн;tу;Gу; су;φу.
Устанавливаем, что оптимизирующей информационной переменной является  tп  - температура приточного воздуха.
На основании функциональной математической модели  пластинчатого рекуператора для расчета используем математический аппарат, который включает в себя систему уравнений, отражающую сущность явлений, протекающих в объекте моделирования, и неравенств, которые определяют область изменения значений независимых переменных. Неравенства являются ограничениями, которые позволяют сформулировать требования, накладываемые на границы изменения характеристик функционирования системы.
Система уравнений включает  5 уравнений: основное уравнение  энергетического баланса (3); уравнения термодинамики (4 -6), уравнение для определения коэффициента полезного действия пластинчатого рекуператора (7):
q1 = q2+ q3,  (3)                                                                  
q1 = суGу (tу – tв) (4)                                           
q2 = сн Gн (tп – tн)  (5)                                          
qм = снGн (tу – tн)(6)   ηр = q2/ qм , (7)                                                                    
где qм - количество тепла, теоретически максимально возможного, получаемого приточным воздухом, с помощью разности температур удаляемого (внутреннего) воздуха и наружного воздуха, т.е. соотношением между теплом, полученным в действительности приточным воздухом, и теоретически максимально возможным полученным теплом.
Берем для примера энергоэффективный дом площадью 280 кв.м  и вводим ограничения:
+15°C < tу< + 25°C;
-20°C < tн< + 30°C;
+10°C < tп< + 15°C;
+16°C < tв< + 18°C;
100 < Gн < 600 м³/час;
100 < Gу < 600 м³/час
В результате решения системы уравнений (3- 7) получаем целевую функцию для определения критерия оптимизации - коэффициента полезного действия пластинчатого рекуператора:
ηр = (tп – tн)/(tу – tн) →  max   (8)                                  
Таким образом, полученная оптимизационная задача с целевой функцией (8), уравнениями (3 - 7) и условиями ограничений представляет собой задачу получения максимального коэффициента полезного действия пластинчатого рекуператора при изменении температуры приточного воздуха tп.
Формулируется оптимизационная задача следующим образом: среди множества допустимых управляющих воздействий  tп , обладающих тем свойством, что соответствующее решение  системы уравнений (3-7) удовлетворяет условиям (ограничениям), найти такие значения tп , которые максимизируют функционал (8).
В результате исследований устанавливаем, что для получения оптимальных режимов работы пластинчатых рекуператоров при низких температурах наружного воздуха и получения высоких значений коэффициента полезного действия, необходим подогрев наружного воздуха перед входом в рекуператор, который приводит к увеличению температуры приточного воздуха  tп [9]. С помощью грунтовых теплообменников можно также решить такую проблему односекционных пластинчатых рекуператоров, как образование конденсата. Из-за выпадения конденсата при низких температурах существует опасность замерзания рекуператора и выхода из строя всей вентиляционной системы. Если расчетные значения температуры наружного воздуха ниже  -10º С, необходимо, в зависимости от предполагаемой влажности вытяжного воздуха, выбрать установку предварительного подогрева воздуха перед рекуператором, которая обеспечит повышение температуры воздуха на входе в рекуператор, или установку байпаса рекуператора с активной защитой от замерзания. Для подогрева наружного воздуха, поступающего в рекуператор, предлагаем использовать грунтовые теплообменники [10].
На основании разработанной математической модели  был определен критерий оптимизации параметров работы пластинчатого рекуператора и установлены оптимальные режимы его работы.}

Литература:

1. Краснов С.А., Краснов В.С., Кряклина И.В., Загребельный М.Н., Лисиенков И.Д. Концепция энергоэффективного интеллектуального дома с ВИЭ  для различных слоев  населения в агломерации мегаполиса // Стратегия развития мегаполиса (некоторые аспекты). Взгляд в 2014 год. Международная конференция. Издательство Информиздат, Москва. 2012. С.48-55.
2. Ивакин Е.К.,  Вагин А.В. Классификация объектов малоэтажного строительства [Электронный ресурс]//  «Инженерный вестник Дона», 2012. № 3. – Режим доступа: http://ivdon.ru/magazine/archive/nly2012/937// (доступ свободный) – Загл. c экрана. – Яз. рус.
3. Магомадова Х.А. Методологические подходы формирования инновационно-инвестиционного механизма средозащитных инноваций в строительном комплексе [Электронный ресурс]//  «Инженерный вестник Дона», 2012. № 4 (часть 2) – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1463// (доступ свободный) – Загл. c экрана. – Яз. рус.
4. Барановский Н.В. Пластинчатые рекуператоры [Текст]/ Н.В. Барановский. -М.: Агропромиздат. 1962.- 210 с.
5. Барон В.Г. Рекуперация тепла в современных системах вентиляции [Текст] // Новости теплоснабжения. –М.: 2006. №6. С. 46-51.
6. Таха, Хемди А. Введение в исследование операций: пер. с англ. М.: Издательский дом «Вильямс», 2001.  912 с.
7. Olesen B.W. A simplified calculation method for checking the indcorclimate// ASHRAE Transactions 98(28). 1983. P. 710-723.
8. Olesen B.Wetal. Thermal comfort in a room heated by different methods// ASHRAE Transactions 86(1). 1980. P. 34-48.
9. Кряклина И.В. Теоретическое обоснование оптимальных режимов работы пластинчатых рекуператоров на основе метода золотого сечения [Текст]// Актуальные проблемы энергетики АПК. Материалы 3 Международной научно-практической конференции. Саратов. СГАУ имени Н.И. Вавилова. 2012. С.127-130.
10. Кряклина И.В. Использование грунтовых теплообменников для повышения энергосбережения рекуперационных систем вентиляции в АПК // Актуальные проблемы науки в АПК. Сборник статей 63-й международной научно-практической конференции.  Кострома. КГСХА. 2012. Т2. С. 107-111.