Нечеткие методы принятия решений поиска объектов на море
Аннотация
Дата поступления статьи: 25.02.2014Рассматриваются некоторые аспекты использования аппарата нечёткой логики для формирования математической модели поиска объектов на море. Описывается порядок использования алгоритма Мамдани для создания модели нечёткого вывода. Даётся пример использования раздела Fuzzy Logic Toolbox пакета Matlab для моделирования работы нечеткой системы поиска и определения оптимального варианта решения задачи на поиск объекта.
Ключевые слова: математическая модель, нечёткая логика, поиск объектов, алгоритм Мамдани, функция принадлежности
05.13.18 - Математическое моделирование, численные методы и комплексы программ
При осуществлении поиска на море действия руководителя поиска - лица принимающего решение (ЛПР) осуществляются применительно к конкретной поисковой ситуации по предписанным процедурам [1], которые можно формализовать в виде элементов математической модели рис.1. Результатом проводимых действий является выбор оптимального способа поиска, позволяющего выполнить поставленную задачу с минимальными затратами.

Рис.1. – Математические модели поиска объектов.
Для формирования математического аппарата модели, поиск можно представить в виде случайного процесса. В реальной обстановке ЛПР присутствует по определению, а объект поиска может осуществлять маневрирование для уклонения. В таком случае рассматривают варианты нормативных и нечетких моделей на основе исследований [2, 3].
Особенность нормативной модели в том, что в зависимости от составляющих той или иной поисковой ситуации (см. рис.1) можно сформировать ее на одном из уровней: детерминированном, стохастическом или неопределенном.
При наличии известных регулярных закономерностей и факторов, имеющих влияние на исход поиска, т.е. при наличии полной и достоверной информации [4] применяют детерминированный уровень нормативной модели.
При наличии достаточного фактического материала для оценки характеристик вероятностных закономерностей поискового процесса (математическое ожидание, дисперсия и т.п.) [5] применяют построение нормативной модели поиска стохастического уровня. Для этого применяются методы статистических испытаний, с использованием оптимизации математического ожидания по критерию эффективности, в качестве основного принципа выбора решения.
В случаях "конфликтной ситуации", при которой объект поиска и поисковые силы придерживаются противоположных стратегий действия и, соответственно, при наличии множества вариантов поисковой ситуации, формируется нормативная модель неопределенного уровня. При этих неопределенностях можно применить теорию нечетких множеств, принципы которых рассмотрены во многих исследованиях, в том числе, при управлении морскими объектами [6 - 8].
В поисковой ситуации в нечетких условиях, поисковым силам ставится задача успешного поиска объектов. Район поиска определен условно, в районе сложные гидрометеорологические условия, запасы для осуществления поиска ограничены. В качестве модели нечеткого вывода для этих целей лучше использовать алгоритм Мамдани, так как созданные на его основе базы знаний являются интуитивно понятными и прозрачными [9,10], по сравнению с другими алгоритмами: Такаги-Сугено, Ларсена, Цукамото [9, 11].
Для того чтобы поиск считался "успешным", необходимо, чтобы он был "быстрым" и "результативным".
В соответствии с исследованием [5] система нечеткого вида создается моделированием вероятности обнаружения за отведенное время поиска рис.2
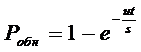 (1)
(1)
где Робн - вероятность обнаружения за отведенное время поиска;
u - производительность поиска, мили2/ч;
t - время поиска, ч;
s - площадь района поиска (в данной работе 1000 миль2).
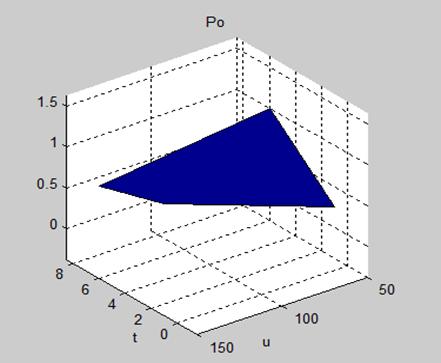
Рис.2. – Вероятность обнаружения за отведенное время поиска.
Понятие быстроты поиска введено, в связи с тем, что в случае спасательной операции людей временной фактор является определяющим. В данном случае задается функция принадлежности, принимающая значение от 0 до 1, которая будет выделять нечеткое множество "быстрых поисков" - T
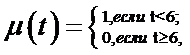 (2)
(2)
где μ(t) - функцией принадлежности "быстрых поисков".
Предельное время пребывания человека в гидрокостюме в воде принято 6 часов, для времени поиска от 1 до 10 часов [12].
Градации времени поиска представлены уровнями:
6 -10 часов - "не быстрый" поиск;
3 - 6 часов - поиск "средней быстроты";
1 - 3 часов - поиск "высокой быстроты".
Для определения множества "успешных поисков" - Р найдем взаимосвязь понятия "результативность" с поисковой производительностью. Расчет поисковой производительности приведен во многих работах, например [13]. Зададимся функцией принадлежности, которая будет выделять нечеткое множество "результативных поисков" - U:
![]() (3)
(3)
где μ(u) - функцией принадлежности "результативных поисков".
Порядок расчета поисковой производительности приведен в руководстве [1], в данной работе диапазон поисковой производительности принят от 50 до 200 мили2/ч, при результативном поиске u > 180 мили2/ч.
Зададимся градацией результативности поиска для данной работы:
50 - 180 мили2/ч - "не результативный" поиск;
180 - 190 мили2/ч - поиск "средней результативности";
190 - 200 мили2/ч - поиск "высокой результативности".
Соответственно, нечеткое множество "успешных поисков" - Р будет находиться на пересечении двух нечетких множеств "быстрых поисков" - T и "результативных поисков" – U, т.е
Р ∈T ∩U, (4)
с функцией принадлежности, оптимизирующей функции принадлежности (2), (3) для любого P:
![]()
![]() , (5)
, (5)
где μ(р) - функцией принадлежности "успешных поисков".
Исходя из выражения (1), зададимся градацией успешности поиска:
Робн ∈ (0 - 0,5] - "не успешный" поиск;
Робн ∈ (0,5 - 0,7] - поиск "средней успешности";
Робн ∈ (0,7 - 0,99] - поиск "высокой успешности".
Определение оптимального варианта решения задачи выполняется моделированием работы нечеткой системы поиска в пакете Matlab с помощью раздела Fuzzy Logic Toolbox [14]. С этой целью для выражения (1) формулируются следующие нечеткие правила выбора решения по поиску:
1. ЕСЛИ t = "не быстрый" И u = " не результативный", ТО р = "не успешный";
2. ЕСЛИ t = "не быстрый" И u = " высокой результативности ", ТО р = "не успешный";
3. ЕСЛИ t = " высокой быстроты " И u = " не результативный", ТО р = "не успешный";
4. ЕСЛИ t = " средней быстроты" И u = " не результативный", ТО р = "не успешный";
5. ЕСЛИ t = "не быстрый" И u = " средней результативности", ТО р = "не успешный";
6. ЕСЛИ t = " средней быстроты " И u = " средней результативности ", ТО
р = "средней успешности";
7. ЕСЛИ t = " средней быстроты " И u = " высокой результативности ", ТО р = "средней успешности";
8. ЕСЛИ t = " высокой быстроты " И u = " средней результативности ", ТО р = " средней успешности ";
9. ЕСЛИ t = " высокой быстроты " И u = " высокой результативности ", ТО р = " высокой успешности ";
На рис.3 приведены результаты нечеткого вывода "успешных поисков" в виде окна визуализации при моделировании процессов поиска в среде Matlab.

Рис.3. – Результаты нечеткого вывода "успешных поисков".
На рис.4 и рис.5 приведены результаты работы синтезированной нечеткой системы по оптимальному выбору вариантов "успешных поисков" в виде поверхности "входы-выход" по выражениям (1)-(5) и правилам нечетких выводов.
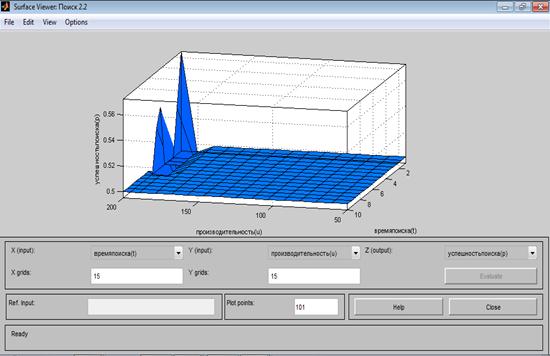
Рис.4. Поверхность "входы-выход" для базы знаний в Surface Viewer.
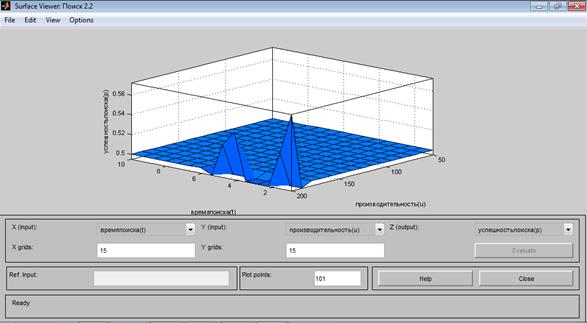
Рис.5. Поверхность "входы-выход" для базы знаний в Surface Viewer.
Сравнивая поверхности результатов поиска на рис.2, 4, 5, можно сделать вывод, что нечёткие правила описывают особенности нелинейной зависимости, а именно:
1. При заданных нечётких правилах, достижение "высокой успешности" не возможно;
2. Возможно достижение "средней успешности" с вероятностью Робн = 0,546, при u = 200 мили2/ч, и t = 2,5 часа;
3. Возможно достижение "средней успешности" с вероятностью Робн= 0,57), при u = 200 мили2/ч, и t = 1 час.
Таким образом, изменяя начальные условия можно добиться получения лучших результатов. Соответственно, использование аппарата нечёткой логики позволяет ЛПР успешно действовать в неопределенных условиях и обеспечивать принятие оптимального решения.
Литература:
1. Руководство по Международному авиационному и морскому поиску и спасению (IAMSAR): Т.2. Координация операций [Текст].- ИМО, 2010.- 474 с.
2. Антонова А.С., Аксенов К.А. Многокритериальное принятие решений в условиях риска на основе интеграции мультиагентного, имитационного, эволюционного моделирования и численных методов [Электронный ресурс]// Инженерный вестник Дона, 2012. №4 (ч. 2) – Режим доступа: http://www.ivdon.ru/magazine/ archive/n4p2y2012/1466 (доступ свободный) — Загл. с экрана. — Яз. рус.
3. Лапыгин Ю.Н. Управленческие решения [Текст]/ Ю.Н.Лапыгин, Д.Ю. Лапыгин.- М.: Эксмо, 2009.- 448 с.
4. Злобина Н.В. Управленческие решения [Текст]. – Тамбов: Тамб. гос. техн. ун-та, 2007.- 80 с.
5. Абчук В.А., Поиск объектов [Текст]/ В.А.Абчук, В.Г.Суздаль.- М.: Советское радио,1977.- 336 с.
6. Бабосюк Н.А., Каргин А.А. Метод вычислительного интеллекта, заимствующий модель взаимодействия молекул внутри клетки [Электронный ресурс]// Инженерный вестник Дона, 2013. №3 – Режим доступа: http://www.ivdon.ru/magazine/ archive/n3y2013/1845 (доступ свободный) — Загл. с экрана. — Яз. рус.
7. Васьков В.А. Методы интеллектуальной поддержки маневрирования судна в стесненных водах [Текст].- Автореф. дисс. на соиск. уч. ст. к.т.н.- Новороссийск: ФГОУ ВПО ГМУ им.адм. Ф.Ф.Ушакова», 2011.- 24 с.
8. Махин В.П. Страшко А.Н. Влияние волнения на движение судна в условиях ветра [Текст].- Эксплуатация морского транспорта. 2010, № 2 (60) - 29 - 31 с.
9. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы [Текст]. – М.: Гор. Линия-Телеком, 2004. – 452 с.
10. Botta A., Lazzerini B., Marcelloni F. New Operators for Context Adaptation of Mamdani Fuzzy Systems [Текст]// Applied artificial intelligence
Proceedings of the 7th International FUNS Conference Genova, Italy 29-31 August 2006. – P. 35-42.
11. Kosko B. Fuzzy systems as universal approximators [Текст] // Proc. 1-st IEEE Int. Conf. On Fuzzy Systems. – San Diego, Ca, 1992. – P. 1163-1170.
12. Международный кодекс по спасательным средствам (Кодекс ЛСА) [Текст].- СПб.: ЗАО ЦНИИМФ, 2004.-156 с.
13. Справочник штурмана/ Под общей ред. В.Д.Шандабылова [Текст]. - М.: Воениздат, 1968.- 544 с.
14. Штобва С.Д. Проектирование нечётких систем средствами MATLAB [Текст].- М.: Горячая линия - Телеком, 2007.- 288 с.