Система расчета равновесного состояния упругой среды, ослабленной плоской симметричной трещиной
Аннотация
Известно, что в настоящее время в промышленности находят широкое применение конструкции, содержащие оболочки, одной из главных причин разрушения которых является наличие неоднородностей, например, трещин. Поэтому задача расчёта элементов конструкций, содержащих неоднородности достаточно широко встречаются в теории упругости и строительной механике. Задача о плоской трещине нормального разрыва в упругом пространстве сведена к решению интегро-дифференциального уравнения, не содержащего оператора Лапласа. Это уравнение позволило получить приближённое решение задачи в форме двукратного интеграла по области, занятой трещиной. Для уточнения полученного решения построен рекуррентный процесс. Результаты вычислений свидетельствуют о его сходимости. Ключевые слова: упругое пространство, трещина нормального разрыва, интегро-дифференциальное уравнение, рекуррентный процесс, коэффициент интенсивности напряжений
Донской государственный технический университет
ВВЕДЕНИЕ
Известно, что в настоящее время в промышленности находят широкое применение конструкции, содержащие оболочки, одной из главных причин разрушения которых является наличие неоднородностей, например, трещин. Поэтому задача расчёта элементов конструкций, содержащих неоднородности достаточно широко встречаются в теории упругости и строительной механике [1 - 3].
Задача о плоской трещине нормального разрыва в упругом пространстве сведена к решению интегро-дифференциального уравнения, не содержащего оператора Лапласа [1]. Это уравнение позволило получить приближённое решение задачи в форме двукратного интеграла по области Ω, занятой трещиной. При этом считается, что область Ω имеет две взаимно-ортогональные оси симметрии, а ограничивающий эту область контур L является достаточно гладким. Для уточнения полученного решения построен рекуррентный процесс, аналогичный предложенному в [2]. Результаты вычислений свидетельствуют о его сходимости. Данное решение является обобщением результатов работы [3], где рассмотрена задача для трещины, форма которой в плане близка к круговой.
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим интегро-дифференциальное уравнение задачи о плоской трещине нормального разрыва в упругом пространстве в виде
(1)
Здесь 
- амплитуда раскрытия трещины; 
- интенсивность нормальной нагрузки, приложенной к берегам трещины; 
, E – модуль Юнга, v – коэффициент Пуассона. Функция удовлетворяет очевидному условию
(2)
Непосредственное интегрирование уравнения (1) и учёт симметрии задачи приводит его к виду:
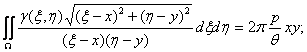(3)
Если кривизна контура L, рассматриваемая как функция дуги S, принадлежит 
, то решение уравнения (3) имеет вид [1]
(4)
где 
- уравнение контура L, ограничивающего область трещины Ω, a – постоянная, имеющая размерность длины.
При сделанных предположениях относительно области Ω функция является четной функцией по обеим переменным. С учетом этого, преобразуем уравнение (3) к виду
(5)
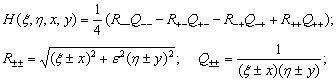(6)
Можно показать, что 
является четной функцией по ε и η и нечетной – по x и y.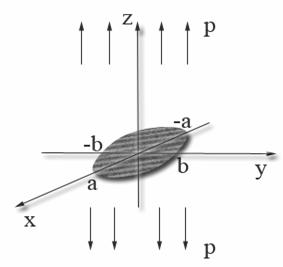
ε – отношение характерных размеров трещины a и b в плане, соответственно, по осям Ox и Oy: 
- интенсивность нормальной нагрузки, приложенной к берегам трещины (рисунок 1);
(рис. 1)
РЕШЕНИЕ
Для решения задачи в безразмерных величинах использована следующая замена переменных
Итерационный процесс определения последовательных приближений функции 
строится по следующей схеме
(7)
(8)
Из предположения о том, что удовлетворяет условию Гельдера по обеим переменным, можно сделать вывод, что выделение в (7) разностных множителей (в отличие от [2]) позволяет устранить сингулярную особенность по одной из переменных. Это приводит к повышению эффективности вычислительного процесса по схеме (7). На осях симметрии функция 
принимает вид
(9)
(10)
Из (9) легко найти
(11)
Интегралы в (9) – (11) могут быть вычислены с использованием формулы Адамара. Соотношения (9) и (10) получены соответствующими предельными переходами (6). Предварительно произведена группировка слагаемых в (6), в результате чего
(12)
где
Интеграл (12) представим в виде суммы интегралов
где
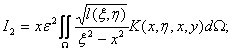
Учтём, что
Здесь также учтено, что область, занятая трещиной, является симметричной относительно обеих осей, ее контур задан уравнением
где m,n – натуральные числа.
При m=2, n=1 имеем
Для повышения эффективности вычисления интеграла 
, область интегрирования 
разобьем на две, выделив внутри круг максимального радиуса 
, т.е. 
, где контур области - определяется уравнением 
В результате для рассматриваемой области получим:
где
Выделим разностный множитель в выражение для 
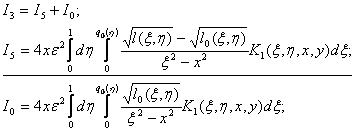
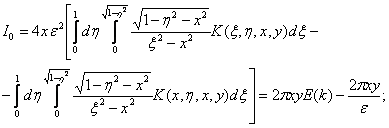
где E(k) – полный эллиптический интеграл 2-го рода,
Итак, суммируя проведённые рассуждения, получим:
(13)
Подставляя выражение (13) в (8), получим начальное приближение
(14)
Вычисление функций 
в схеме (7) осуществлялось по следующей методике. Рассчитывались значения функций 
в узлах равномерной сетки 
, после чего функция 
в интегралах (7) заменялась интерполяционным многочленом Лагранжа
(15)
ЗАКЛЮЧЕНИЕ
Задача о плоской трещине нормального разрыва в упругом пространстве решена на основе интегро-дифференциального уравнения (1). Нулевым приближением решения является уравнение (14). Для уточнения полученного решения построен рекуррентный процесс (7).
ЛИТЕРАТУРА
[1] Александров В.М., Сметанин Б.И., Соболь Б.В. Тонкие концентраторы напряжений в упругих телах. М.: Физмалит, 1993. 224 с.
[2] Сметанин Б.И., Соболь Б.В. Равновесие упругого слоя, ослабленного плоскими трещинами //ПММ.1984.Т. 48. Вып. 6. с. 1030-1038.
[3] Рашидова Е.В., Сметанин Б.И., Соболь Б.В. Равновесная плоская симметричная трещина в неограниченной упругой среде. В кн.: Одиннадцатая международная конференция «Современные проблемы механики сплошной среды». Ростов-на-Дону, ЮФУ, 2007 г.
20 июня 2008 г.