Имитационное моделирование потоков пешеходов на основе модели социальных сил

Аннотация

И.О. Яловой

Описана предметная область исследования — поведение пешеходов в сложных ситуациях. Дан концептуальный обзор модели социальных сил и её последующей разработки. Обсуждается инструментарий разработки, проводится верификация модели и последующий анализ экспериментов, проведенных с её помощью. Представлена разработанная среда имитационного моделирования потоков пешеходов, позволяющая создавать, конфигурировать, отлаживать, исполнять эксперименты на основе модели социальных сил, а также получить необходимые статистические данные для последующего анализа.
Ключевые слова: модель социальных сил, потоки пешеходов, движение пешеходов, поведение пешеходов, имитационная модель, многоагентная модель, моделирование. № гос. регистрации 0420900096\0008

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Введение

Невозможно эффективно спланировать транспортный узел или массовое мероприятие без знаний о поведении пешеходов. Поведение пешеходов является сложным феноменом, поэтому необходимо имитационное моделирование при планировании объектов с высокой плотностью пешеходов и ограниченным пространством для оптимизации потока пешеходов и гарантированного предотвращения давки в случае паники.
За последние сорок лет было предложено несколько моделей для моделирования потоков пешеходов. Одна из таких моделей это модель социальных сил, которая описывает несколько феноменов, наблюдаемых при движении пешеходов. Эта модель была выбрана для реализации, так как является непрерывной, многоагентной, позволяет менять точность в зависимости от выбранного численного метода. Её единственным существенным недостатком является низкая производительность при реализации на ЭВМ.

Модель социальных сил

Полное, детальное изложение модели социальных сил превышает рамки статьи, но любой желающий может ознакомиться с ней [1,2,3,4] и её модификациями [5], дадим лишь необходимую информацию.
Модель социальных сил была разработана D. Helbing и P. Molnar [1]. В этой модели различные мотиваторы и воздействия на пешехода выражены в форме различных сил, показанных на рис. 1.

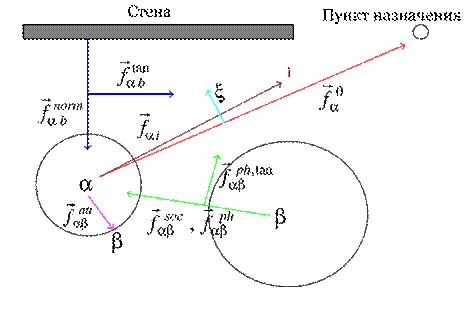
Рис.1. График модели социальных сил пешехода

Модель использует Ньютоновскую динамику для описания движения пешеходов. Модель демонстрирует несколько естественных поведенческих феноменов пешеходов в процессе движения:

1. Пешеходы выбирают самый короткий путь;
2. Пешеходы двигаются с индивидуальной скоростью, с учетом ситуации, пола, возраста, ограничений;
3. Пешеходы держаться на определенном расстоянии друг от друга. Дистанция зависит от плотности потока пешеходов и скорости движения.

Движение пешехода в модели социальных сил описывается суммой действующих на него сил. Решая полученную систему дифференциальных уравнений, можно узнать положения в пространстве, скорость и ускорение пешехода в любой момент времени. Существует множество численных методов для решения дифференциальных уравнений: метод Эйлера, метод предиктора-корректора, методы Рунге-Кутта, методы Гира. Они различаются по производительности и точности, имеет смысл подбирать метод для конкретной задачи. Суммарная социальная сила, действующая на пешехода, зависит не только от его положения в пространстве, но и от его скорости, поэтому метод Гира пятого порядка является оптимальным для данной задачи.

Имитационное моделирование

Реализация модели социальных сил на ЭВМ представляет собой нетривиальную задачу. Было предпринято немало попыток, все они представляют собой компромисс между точностью и скоростью.
Как и любая другая имитационная модель, она выполняется в цикле, пока не будет достигнуто условие остановки. Упрощено алгоритм выглядит следующим образом:

1. Установить параметры модели
2. Если условие окончания цикла недостигнуто, то
   1. Для каждого пешехода
      1. Рассчитать движущую силу
      2. Для всех других пешеходов
         1. Рассчитать социальную силу
         2. Добавить её к движущей силе
      3. Для всех стен и препятствий
         1. Рассчитать силу взаимодействия
         2. Добавить её к движущей силе
      4. Рассчитать новые значения положения, скорости и ускорения пешехода
3. Окончание цикла

После установки параметров модели, управление передается в основной цикл, в котором вычисляются силы, действующие на каждого пешехода. Чтобы рассчитать силу, действующую на каждого пешехода, необходимо просуммировать силы от всех других пешеходов, стен, препятствий и аттракторов, что приводит к сложности алгоритма . Сложность алгоритма  достаточно требовательна к ресурсам ЭВМ, при том, что некоторые модели потоков пешеходов имеют сложность n.
Модель социальных сил была реализована с использование среды разработки Microsoft Visual Studio 2008 на языке программирования C# с использованием фреймоворка WPF. Конфигурация компьютера на котором проводились эксперименты, представлена ниже:

1. Операционная система: Microsoft Windows Vista;
2. Процессор: Intel® Core™ 2 CPU 4300 @1.8GHz;
3. Оперативная память: 4GB DDR2 PC6400 Hynix;
4. Видео карта: NVIDIA GeForce 9600 GT.

Для постановки эксперимента необходимы эмпирические данные, которые были взяты из работ [1,2]. Ввиду большого количества параметров не будем рассматривать их все в данной статье, лишь укажем самые важные. В соответствии с данными из работ [1,2] скорость пешеходов распределена по нормальному закону с медианой 1.34 м/c и стандартным отклонением 0.26 м/c. Пешеходы входят в помещение в случайных позициях.
Первый эксперимент моделирует движение двух встречных потоков пешеходов по просторному коридору. На рис.2 показано одно из состояний модели в процессии работы.

Рис.2. Иллюстрация эксперимента движение двух встречных потоков пешеходов по просторному коридору

Мы видим сформированные, так называемые, полосы движения, несмотря на то, что движение пешеходов начинается в случайных позициях. Движение полосами оптимально, что подтверждается жизненным опытом и математическими расчетами. Каждый пешеход руководствуется достаточно простыми правилами при движении, но явления демонстрируемые системой выходят за рамки поведения пешеходов. Такие явления самоорганизации проявляются в многоагентных системах, какой модель социальных сил и является. Данный феномен был зафиксирован многими исследователями движения поток пешеходов и исследователями модели социальных сил в частности, что говорит в пользу правильности её реализации.
Следует также отметить, что количество полос движения линейно зависит от ширины коридора.
Во втором эксперименте демонстрируется прохождение дверного проема в коридоре двумя встречными потоками пешеходов. На рис.3 видно, что в то время, пока один поток пешеходов проходит через дверной проём, другой поток вынужден ждать. Но через некоторое время инициатива поменяется. Такое явление самоорганизации получило название колебание инициативы потоков пешеходов. Оно хорошо подтверждено как наблюдателями, так и исследователями.

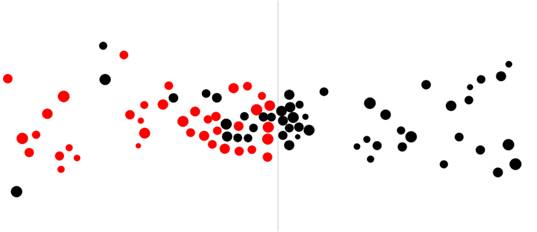
Рис.3. Иллюстрация эксперимента прохождения дверного проема в коридоре двумя встречными потоками пешеходов

Программное обеспечение для моделирования потоков пешеходов

Для создания экспериментов, обсуждаемых ранее, была разработана программа. Она позволяет создавать и проводить эксперименты на основе модели социальных сил. На рис.4 представлен интерфейс это программы. Созданная программа носит экспериментально-научный характер и поэтому не удовлетворяет критериям коммерческого программного обеспечения. Существуют коммерческие программы для моделирования потоков пешеходов, такие как Vissim, SimWalk, Anylogic и.т.д. Несмотря на очевидно превосходство этих программ над собственными разработками, стоит отметить, что при разработке собственной модели с «нуля», разработчик получает полный контроль, как над моделью, так и над проведением экспериментов, сам определяет дальнейшие направления развития, закладывает базу под дальнейшие возможные коммерческие разработки, исключает зависимость от какой либо компании.

Рис.4. Интерфейс программы компьютерных экспериментов на основе модели социальных сил

Заключение

Разработанная имитационная модель описывает движение потоков пешеходов в пространстве, демонстрируя несколько явлений, которые являются результатом самоорганизации и не заложены в поведение пешеходов. Полученная модель верифицирована при помощи типовых экспериментов, результаты которых совпали с результатами других исследователей, эмпирическими данным и наблюдениями.
Разработана среда для создания, модификации, исполнения и отладки имитационной модели потоков пешеходов на основе модели социальных сил. Создан графический интерфейс пользователя, который позволяет легко осуществлять операции над моделью. Визуальное представление хода эксперимента позволяет непосредственно наблюдать за движением пешеходов и событиями.
Полученная имитационная модель предоставляет практическую пользу для ученных и инженеров заинтересованных в моделирование движения пешеходов. С её помощь возможна дальнейшая разработка модели социальных сил, конструкций улучшающих пропускную способность и повышающих уровень безопасности, анализ и прогнозирование поведения пешеходов на массовых мероприятиях и в транспортных узлах.

Библиографический список

1. Helbing, D. et al, Social force model for pedestrian dynamics, Physical review E, May 1995 .
2. Helbing, D. et al, Simulation of Pedestrian Crowds in Normal and Evacuation Situations, Pedestrian and Evacuation Dynamics Springer-Verlag, Berlin; Heidelberg; New York (2002) pp. 21-58.
3. Helbing, D. et al, Simulating dynamical features of escape panic, Nature, v. 407, pp 487-490, 2000.
4. Helbing, D. et al, Self-organization phenomena in pedestrian crowds, in Self-Organization of Complex Structures: From Individual to Collective Dynamics, pp. 569-577, F. Schweitzer (Ed.) (Gordon and Breach, London, 1997).
5. Lakoba, T. I. et al, Modifications of the Helbing-Molnár-Farkas-Vicsek Social Force Model for Pedestrian Evolution, Simulation, 2005, 81, pp. 339-352