Метод выбора оптимальной стратегии развития фирмы

Аннотация

Л. В. Долятовский

Поставлена задача выбора оптимальной стратегии развития фирмы на основе комбинации ее объемных и структурных изменений. Задача решена методом множителей Лагранжа путем построения функции зависимости прибыли от объемных и структурных изменений. Показано практическое применение разработанного метода.
Ключевые слова: Развитие фирмы, стратегия развития, комбинация объемных и структурных изменений, оптимизация стратегии, метод множителей Лагранжа, эффективность изменений.

08.00.13 - Математические и инструментальные методы экономики

Поставлена задача выбора оптимальной стратегии развития фирмы на основе комбинации объемных и структурных изменений. Задача решена методом множителей Лагранжа. Показано практическое применение разработанного метода.
Задача выбора стратегии развития фирмы становится все более важной в условиях возрастания нестабильности внешней среды и необходимости обеспечения экономической устойчивости фирмы. Имеется несколько подходов к задачам обоснования стратегии развития, Ильенкова предлагает учитывать структурные сдвиги во внешней среде [1], Я.В. Гамалей отмечает важность качественных изменений в экономике региона [2], предложено формировать стратегию развития путем комбинации объемных и структурных изменений [3]. Однако полностью эта задача не решена, в статье приведена формальная постановка и решение задачи обоснования оптимальной стратегии развития.

1. Основные концепты теории развития.

Современное предприятие на всех фазах жизненного цикла реализует два взаимосвязанных процесса: функционирование и развитие (рис.1).

Рис. 1 – Процессы жизненного цикла предприятия

Функционирование заключается в выполнении заданных функций производства и получения конечных результатов. Развитие направлено на адаптацию предприятия к изменяющейся внешней и внутренней среде, именно эти процессы обеспечивают экономическую и финансовую устойчивость предприятия. Особую роль играют качественные изменения, заключающиеся либо в применении  структуры деятельности (например, номенклатуры производимой продукции), либо в радикальных изменениях качества деятельности (внедрении принципиально новых технологий, инноваций, систем управления).
Опыт последних лет показывает часто большую эффективность качественных изменений по сравнению с увеличением выпуска продукции.
Развитие повышает устойчивость предприятия, функционирование которого определяется s-образным законом (рис.2)

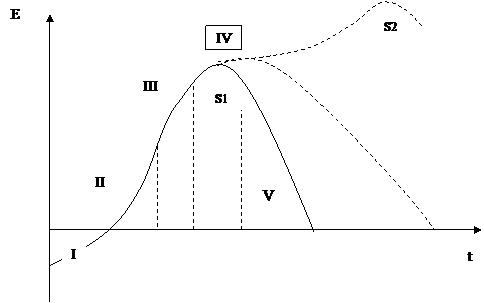
Рис. 2 – Кривая жизненного цикла фирмы

Ввиду конечного характера жизненного цикла предприятия для повышения его устойчивости применимы два способа: 1) продление участка насыщения за счет структурных изменений, 2) радикальные качественные изменения при переходе на новую s-образную кривую (S₁→ S₂). Таким образом, продлить жизненный цикл предприятия можно за счет количественных q_i и структурных φ_i изменений, причем одинаковый результат (например, размер прибыли) можно получить при разных комбинациях этих факторов (рис.3), определенных линиями равной прибыли (изопрофитами).

Рис. 3 – Положение изопрофиты фирмы

Уравнение изопрофиты можно записать в виде:
,   (1)
где α, β – эластичности факторов развития.
,  (2)
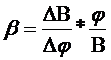 ,      (3)
Задача выбора стратегии развития фирмы состоит в определении такой комбинации (q*, φ*), которая обеспечит максимальное значение прибыли при ограничении затрат на изменения q и φ.

2.Постановка задачи выбора стратегии развития.

Для определения оптимальной стратегии развития предприятия нужно выбрать такие значения структурных сдвигов φ* и количественных изменений q*, которые обеспечат достижение максимума прибыли предприятия:
,   (4)
при ограничениях  с₁q+c₂ φ ≤ C_доп,  q≥0, φ ≥0.
Графическое решение этой задачи определяется точкой касания изопрофиты и изокосты (рис.3). возникает вопрос определения эластичностей α и β. Их значение можно рассчитать либо методом наименьших квадратов на основе таблицы значений В, q и φ, либо по формулам (2), (3) на основе эмпирических данных предприятия. При этом структурные сдвиги φ имеют четыре показателя (рис.4).

Рис. 4 – Показатели структурных сдвигов

Для решения задачи (4) используем линейный коэффициент абсолютных сдвигов, характеризующий средний сдвиг структуры портфеля в анализируемый период по сравнению с базовым: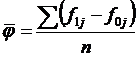
,      (5)
где f_0j, f_1j – начальные и конечные частоты j-той продукции в портфеле фирмы,
n – номенклатура изделий.

3.Пример решения оптимизационной задачи.

Для рассматриваемого примера на основе статистических данных рассчитана изопрофита в виде уравнения:
,     (6)
И определена изокоста:
,    (7)
Аналитическое решение оптимизационной задачи (4) можно найти методом множителей Лагранжа. Записываем лагранжиан в виде:
,   (8)
и находим его частные производные:
,    (9)
Для конкретного примера имеем:
,   (10)

Разделив (11) на (12) имеем:
,    - оптимальное соотношение факторов развития.
Из уравнения (12):
35-3*0,57φ-10φ=0.
Оптимальные значения факторов равны:
φ*=2,98
q*=7,13.
То есть, необходимо изменить структуру производства на 2,98%, чтобы получить В=мах. Таким образом, оптимальная стратегия имеет вид: S*=(q*; φ*)=(7,13;2,98)%, и тогда Вмах=q^2,5φ^4,3=7,13^2,5*2,98^4,3=14,85 млн. рублей.
Таким образом, анализ реальной статистики работы предприятия при изменениях объемов и структуры выпускаемой продукции дает возможность определить эластичности факторов развития и найти такую их комбинацию, которая обеспечивает максимальный эффект работы предприятия.

Литература

1.Ильенкова С. Д., Инновационный менеджмент. - М. - Инфра-М, 2005, 234с.
2.Долятовский В.А., Толстых Т. Н., Гамалей Я.В. Моделирование процессов управления региональной экономикой – Тамбов: ТГУ, 1998, 314с.
3.Долятовский Л.В. Оптимизация стратегии развития фирмы // Молодежь и наука: Реальность и перспективы. – Невинномысск: НИЭУП, 2011, 542с.