Числовые характеристики релаксации напряжений в пропитанном растворами песчаном бетоне

Аннотация

Г.Г. Смелик, А.К. Сысоев, О.Я. Печикин

Исследовалась кинетика релаксации напряжений в песчаном бетоне, пропитанном растворами петролатума в дизельном топливе и полиэтилгидроксилоксановой жидкости 136-41 в керосине в возрасте 7, 14 и  28 суток с помощью контрактометра – релаксометра.
Экспериментальные тренды практически совпадают с вычисленными значениями по предлагаемой формуле с дробной степенью времени. Параметры функциональной зависимости определены по предложенной методике с помощью компьютера на базе 10–суточного эксперимента. Кроме этих параметров и выборочного коэффициента линейной корреляции для количественной и качественной характеристики кинетики релаксации напряжений предлагаются известные в теории вероятностей и математической статистике числовые характеристики.  
Ключевые слова: компьютер, контрактометр – релаксометр, коэффициент затухания, песчаный бетон, релаксация, статистические характеристики.

05.23.05 - Строительные материалы и изделия

Для цементных бетонов характерно непрерывное взаимодействие с окружающей средой и изменение с течением времени внутренней структуры.
В отличии от свойств упругого тела, характеризующегося мгновенным возникновением деформаций при приложении к нему нагрузки и мгновенным восстановлением их после снятия нагрузки, ползучесть – замедленная деформация нагруженного тела, нарастающая со временем. С явлением ползучести непосредственно связано явление релаксации напряжения при постоянной нагрузке.
Известно, что для повышения коррозийной стойкости изделий из бетонов их пропитывают растворами кремнийорганических соединений, петролатума и других веществ [1].
Пропитка цементных бетонов очевидно влияет и на кинетику релаксации, поэтому для получения числовых характеристик влияния пропитывания образцов из песчаного бетона на релаксируемость и были выполнены описываемые ниже эксперименты.
Релаксация напряжений исследовавшихся образцов измерялась с помощью контрактометра – релаксометра [2], работающего по принципу компенсации деформаций изменением механической нагрузки. Создаваемая деформация (прогиб балочек) вызывалась в начале нагрузкой, равной 30 % от разрушающей. Конструкция прибора дает возможность получить кривую, характеризующую падение напряжений в нагруженном образце при поддержании заданной величины деформации.
Пропитка образцов из песчаного бетона осуществлялась путем окунания их в растворы петролатума в дизельном топливе, полиэтилгидросилоксановой жидкости 136-41 (ГОСТ 10834).
Песчаный бетон для образцов изготавливался на портландцементе Новороссийского завода «Октябрь» марки 400 с плотностью 3,1 г/см и нормальной густотой 25%, заполнителем являлся песок Донского карьера Ростовской области с модулем крупности Мкр=1,38.
Состав бетона принят 1:1,82, при В/Ц=0,34 (расход цемента 730 кг, песка – 1339 кг на 1 м). Предел прочности при сжатии 320 кг/см, а при изгибе R=6,9 Мпа, динамический модуль упругости  Мпа.
Исследования проводились на образцах 20х20х240 мм, в течение 28 суток твердевших на воздухе (с промежуточными испытаниями 7, 14 и 28 суток).
Пропитка 14 суточных образцов производилась 30 минутным окунанием их в растворы полиэтилгидросилоксановой жидкости 136-41 в керосине (1:20), петролатума в дизельном топливе (1:4). После суточного хранения на воздухе эти образцы подвергались загружению на контрактометре – релаксометре. Пропитка 7 суточных образцов производилась только раствором полиэтилгидросилоксановой жидкости 113-63. Затем после 1, 7 и 28 суточного хранения на воздухе эти образцы подверглись испытанию, т.е. загружению на контрактометре – релаксометре.
Одновременно с этими составами изготавливались образцы – кубы размером 50х50х50 мм для определения открытой пористости. Открытая пористость для непропитанных образцов составила –0,15. пропитанная петролатумом –0,09 и кремнийорганической жидкостью – 0,076.
Как показывает анализ результатов, наибольшей способностью к релаксации обладают непропитанные образцы. Пропиточный материал блокирует испарение влаги из образца, увеличивает вязкость структуры, вследствие чего у пропитанных образцов скорость релаксации снижается.
Наименьшей она оказалась у пропитанных раствором петролатума. Промежуточная – у пропитанных раствором 113-63. Снижается скорость релаксации напряжений и с возрастом образцов за счет заполнения пор гидратными новообразованиями.
Кинетика релаксации напряжений хорошо описывается функцией [3]
,     (1)
где  – коэффициент затухания релаксирующих напряжений, вычисленный в момент времени ;
 – возраст бетона в момент загружения;
 – постоянная, характеризующая промежуточное положение гелевой составляющей бетона между телами Гука и Ньютона ;
 – постоянная, характеризующая скорость релаксации напряжений (особенно в начальной промежуток времени).
Вычисление параметров  и  выполнялось по матрице экспериментальных данных релаксации напряжений:
,                   
,                          
где ;
 – число экспериментальных пар точек;      
,  ,
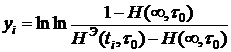 – экспериментальное значение коэффициента затухания в момент времени  .
Оптимальные значения ,  и  вычислялись на компьютере по разработанной нами программе, написанной на различных алгоритмических языках. Критерием оптимальности служил принцип Лажандра, по которому сумма квадратов разностей опытных значений  и вычисленных по формуле (1) должна быть наименьшей. Компьютер затрачивает на обработку одной матрицы экспериментальных данных 6 секунд.
Сравнение вычисленных по формуле (1) и экспериментальных определений релаксирующих напряжений, приведенное в таблице 1, показывает, что во все моменты наблюдений погрешность расчетных величин  не превышает 3% от опытных, то есть экспериментальные тренды практически совпадают с расчетными кривыми. Об этом же свидетельствуют значения выборочного коэффициента линейной корреляции  между  и  , приведенные в таблице 2, которые, как правило, превышает 0,99, то есть очень близки к единице.
Вычислением  выполнялось по формуле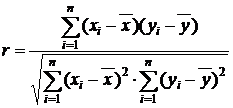
 ,               
где , .
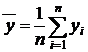Таким образом, функция (1) с большей точностью описывает кинетику релаксации напряжений в песчаном бетоне. Следовательно, она позволяет прогнозировать с помощью компьютера предельное значение коэффициента затухания  и экстраполировать величины  на основе опытных наблюдений в течении конечного отрезка времени. Это прогнозирование выполнено в настоящей работе на базе 10-суточного эксперимента (таблица 2).
Равенство (1) можно представить в виде
,                     
где  – нормированный коэффициент роста отрелаксированной части напряжений к моменту времени .
Величина  монотонно возрастает от 0 до 1 и представляет собой известную в теории вероятностей и математической статистике интегральную функцию распределения времени релаксации [4]. Это позволяет ввести для количественной и качественной характеристики релаксации напряжений, кроме параметров уравнения (1) и коэффициента корреляции , статистические характеристики: математическое ожидание , медиану , среднее квадратическое отклонение , которые вычислялись по формулам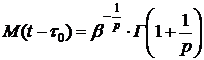
,                              
,                                     
,                   
где 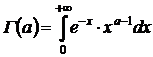 – гамма – функция.
Математическое ожидание – это средневзвешенное время релаксации напряжений или иначе абсцисса центра группирования распределения релаксирующих напряжений, которое характеризует релаксационную податливость бетона во всем диапазоне времени релаксации: чем меньше , тем бетон более релаксационно податлив.
Среднее квадратическое отклонение  характеризует релаксационную устойчивость бетона. Чем больше , тем больше разброс времени релаксации, то есть тем в течение большого промежутка времени бетон способен к значительной релаксации напряжений. Медиана  распределения – это время, за которое напряжения в бетоне релаксируют на величину, равную 50 % от .
Численные значения параметров функции (1) и статистические характеристики для всех опытов приведены в таблице 2. Только непропитанные образцы, загруженные в возрасте =7 сут, отрелаксировали напряжения более, чем на половину от начального напряжения , а наибольшие предельные значения коэффициента затухания показали образцы опытов 3, 8, 9, соответственно 0,74; 0,77 и 0,74. Существенно отличается от других кинетика релаксации напряжений непропитанных образцов (опыт 1). Структура этих образцов оказалась наиболее далекой от структуры идеального вязкоупругого тела , что свидетельствует о преобладании кристаллических контактов по сравнению с коагуляционнонными. Через шесть часов после испытания напряжения в этих образцах уменьшилась на половину общей части отрелаксировавших напряжений за весь диапазон времени . Напряжения в образцах остальных восьми опытов достигли 50%  уровня только через 9 и более часов.
Значение  сут. Для образцов первого опыта свидетельствует об их наихудшей релаксационной податливости, а величина  – о наибольшей релаксационной устойчивости.
Экспериментальное определение величин релаксируемых напряжений показало, что образцы, пропитанные 136-41 (опыт 2) и петролатумом (опыт 3),  занимают среднее положение между идеально упругим и вязкоупругим телами соответственно  и , причем образцы, пропитанные петролатумом, обладают меньшей релаксационной устойчивостью , чем пропитанные  136-41 в керосине . Наилучшую релаксационную податливость обнаружили непропитанные образцы, загруженные в возрасте =28 сут. , эти же образцы обладают наименьшей релаксационной устойчивостью .
Кинетика релаксации напряжений непропитанных и пропитанных 134-41 образцов, загруженных после суточного хранения на воздухе в возрасте 7 сут., существенно отличается от других. Предельное значение коэффициента затухания для непропитанных образцов оказалось меньше, чем для пропитанных (соответственно 0,46 и 0,51), релаксационная податливость первых  меньше последних , но релаксационная устойчивость у них примерно одинаковая ( и ), причем структура пропитанных образцов оказалась наиболее близкой к идеальному вязкоупругому телу . Есть основания утверждать, что существует некоторый возраст загружения =7  сут. такой, что пропитанные и непропитанные образцы имеют одинаковый коэффициент затухания . Существование этих экстремальных точек ранее обнаруживалось при изучении влияния других факторов (температура, влажность, размеры и др.) на кинетику длительных процессов в бетонах, особенно раннего возраста. Причинами этого является интенсивно продолжающаяся гидратация цемента и влияние на нее механической нагрузки, различное время хранения образцов на воздухе после пропитки, влияние напряжения от высыхания при испытании.    

 Таблица 1.

Сравнение расчетных по формуле (1) и экспериментальных определений
релаксирующих напряжений в песчаном бетоне

Таблица 2.

Параметры формулы (1) и статистические характеристики
кинетики релаксации напряжений песчаного бетона

Выводы

  1. Деформация ползучести цементно – песчаного бетона, пропитанного растворами различных импрегнирующих составов уменьшается, что объясняется блокировкой влаги внутри бетона и затруднительной вследствие этого текучестью гелевой структурной  составляющей цементного камня.
2. Сушка бетона способствует значительному изменению гелевой составляющей цементного камня и ускоренной кристаллизации новообразований, что снижает ползучесть бетона.
3. Сравнение расчетных и эксперементальных определений релаксируемых напряжений в песчаном бетоне показывает, что погрешность вычисленных величин коэффициента затухания  не превышает 3% от опытных, то есть экспериментальные тренды практически совпадают с расчетными кривыми. Формула (1) позволяет прогнозировать предельные величины  с помощью компьютера на базе экспериментальных данных, полученных за относительно короткий срок испытания загруженных образцов.

Литература

  1. Печикин О.Я., Минас А.И. и др. Исследование стойкости песчаного бетона в условиях, способствующих развитию солевой формы коррозии. /Долговечность строительных материалов и конструкций. – Ростов н/Д : РИСИ, 1977.
2. Дибров Г.Д., Остриков С.М. и др. Исследование внутренних напряжений в дисперсных структурах, развивающихся при замораживании. //ДАН СССР, 187,2.–М.: 1969.
3.Полисмаков А.И., Смелик Г.Г., Сысоев А.К. Математическая модель релаксации напряжений в бетоне. //Известия Северо-Кавказского научного центра высшей школы. Технические науки.–1984, №2.
4. Хрущева И.В., Щербаков В.И., Леванова Д.С. Основы математической статистики и теории случайных процессов. – Спб.:  Лань, 2009.