Дефектоскопия стальной проволоки методом тензорной магнитной топологии
Аннотация
Описана методика исследования топологии тензорных величин магнитного поля рассеяния естественных дефектов при естественном намагничивании геомагнитным полем, на основе которой реализован цифровой холловский дефектоскоп. С его помощью удалось зарегистрировать дефекты с характерным размером от 15 мкм в стальной проволоке, используемой для навивки пружин амортизаторов грузовых автомобилей.
Ключевые слова: Неразрушающий контроль, датчик Холла, магнитная томография.Ключевые слова:
Приоритетным направлением в области неразрушающих методов контроля является создание систем компьютерной диагностики, обеспечивающих классификацию дефектов в процессе автоматизированного контроля. Параметры дефектов можно определить путем подбора параметров математической модели, описывающей поле рассеяния дефекта [1]. В настоящее время достаточно точное решение прямой задачи магнитостатики получено для внешнего дефекта типа бесконечно длинной прямоугольной канавки [2] и для внутреннего дефекта типа цилиндрического сверления [3]. Однако поля рассеяния реальных дефектов значительно отличаются от теоретических двумерных моделей [4]. В этом случае эффективны методы распознавания образов [5], например, на основе обучающих эталонов [6], когда рассматриваются признаки, позволяющие делать вывод о наличии или отсутствии дефекта в образце по топологии измеренных компонент магнитного поля [7]. По существующим представлениям определение параметров дефекта при этом потребует повышения информативности измерений, то есть существенного увеличения, как числа точек измерений, так и количества величин, определяемых в каждой точке [8]. В случаях, когда важно знать не только примерный суммарный объём дефектов, но и определить их количество, возникает проблема разрешения дефектов [7], которую можно решить, имея максимально точную информацию о микротопологии поля.
Необходимую информативность измерений в задачах магнитной дефектоскопии может обеспечить анализ топологии тензорных величин магнитного поля рассеяния. Так, в задаче магнитной пеленгации определение координат дипольного источника поля основано на измерении пространственных производных компонент вектора магнитной индукции, создаваемой этим источником в окрестностях точки наблюдения [9]. По измеренным пространственным производным, образующим тензор, определяют направление на диполь, а затем вычисляют магнитный момент диполя, и расстояние до него [9, 10]. Разумеется, поле рассеяния внутреннего дефекта с учетом поверхностных и объемных магнитных зарядов может быть существенно сложнее, чем в дипольном приближении [11], но есть основания полагать, что измеренная с высоким пространственным разрешением топология тензорных величин полей рассеяния может использоваться как обучающие эталоны для построения экспертных систем распознавания и классификации дефектов [12 – 15].
В качестве примера применения метода тензорной магнитной топологии рассмотрим задачу обнаружения дефекта в продольно намагниченном стержне. На производстве к такой задаче сводится магнитная дефектоскопия стальных прутков, труб [16], тросов, канатов [17] и т. д., которая производится при намагничивании исследуемого изделия до технического насыщения, когда магнитная проницаемость практически постоянная, а намагниченность однородна. В таких условиях поля рассеяния велики в сравнении с полем Земли, что упрощает регистрацию дефектов. Вместе с тем, необходимость намагничивать объект контроля до состояния технического насыщения существенно затрудняет построение автоматизированных комплексов магнитометрического неразрушающего контроля, сочетающих технологичность и высокую производительность с возможностью оперативного контроля инженерных конструкций путем дистанционного опроса системы датчиков, установленных в критических точках.
Отказ от технического насыщения усложняет идентификацию дефекта, в зависимости от ориентации объекта контроля относительно вектора геомагнитного поля его намагниченность и поле рассеяния дефекта могут значительно изменяться. С другой стороны, в слабых полях, сравнимых с полем Земли, нелинейность кривой намагничивания приводит к возникновению объемных магнитных зарядов и их добавочных полей. В результате связанный с дефектом магнитный диполь оказывается вытянутым, иногда в сотни раз, вдоль направления намагниченности, и приближенным к границе изделия [18 – 20], что улучшает разрешение внутренних дефектов микронных размеров при обеспечении необходимой чувствительности магнитных измерений.Анализ тензорных компонент поля рассеяния, наиболее чувствительных к структурным неоднородностям, можно выполнить в рамках модельной задачи об эквивалентном диполе в вакууме, которую удобно рассмотреть в цилиндрической системе координат. В слабых намагничивающих полях длинный стержень будет намагничен продольно, и эквивалентный дефекту диполь будет направлен вдоль оси стержня [21]. Пусть эквивалентный диполь располагается в точке с цилиндрическими координатами z = z1, ρ = rd, θ = 0. Радиальная, тангенциальная и продольная компоненты индукции магнитного поля в точке наблюдения на поверхности стержня радиуса R имеют вид:
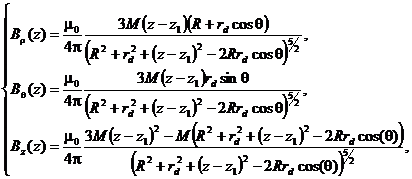
где M – эквивалентный магнитный момент диполя. Заметим, что компоненты поля рассеяния быстро затухают с удалением от диполя, следовательно, регистрацию дефектов следует производить при минимальном удалении от поверхности объекта контроля. Наибольший интерес для исследования представляет радиальная компонента поля, поскольку она существенно меньше зависит от угла θ, чтобы минимизировать зависимость от угла следует использовать в качестве индикатора наличия дефекта сумму сигналов трех магнитометрических датчиков, расположенных на окружности под углом 120° друг относительно друга. Несложно показать, что в однородном поле при одинаковой крутизне преобразования датчиков при любом угле поворота такой системы датчиков сумма будет равна нулю, а продольная компонента градиента суммы сигналов с трех датчиков равна
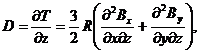 |
(1) |
где T(z) = Bρ(z, R, θ) + Bρ(z, R, θ+2π/3) + Bρ(z, R, θ+4π/3) = 3R(∂Bx/∂x + ∂By/∂y)/2, R – радиус стержня, θ – азимутальный угол первого датчика, отсчитанный от прямой, соединяющей дефект с осью z, а производные взяты в начале координат.
Известно, что любой магнитометрический датчик, вообще говоря, измеряет среднеинтегральное по некоторому объему значение поля, причем, чем меньше размер датчика, тем выше точность определения производной поля. Феррозонд, обеспечивающий необходимую чувствительность, имеет сравнительно большой объем, кроме того, он возмущает поле в значительной окрестности. Поэтому для исследования тензорных величин магнитного поля феррозонды не пригодны, так как из-за взаимного влияния их нельзя располагать близко. Более удобен для микромагнитной томографии пленочный датчик Холла.
Обычно считается, что такой датчик измеряет среднеинтегральное по площади чувствительного элемента значение магнитной индукции [23, 24]. Проведенные нами исследования показали, что пространственное разрешение датчика Холла на порядок меньше размеров самого чувствительного элемента, то есть составляет 0,1 мм, и его сравнительно несложно значительно улучшить [25]. Систематические погрешности датчика Холла, обусловленные остаточным напряжением, смещением измерителя, а также магнитным полем управляющего тока датчика также исключаются применением специального алгоритма измерений [26].
Натурные исследования компонент поля рассеяния проведены разработанным трехканальным нанотеслометром, датчик которого содержит три преобразователя Холла ПХЭ602117А с крутизной преобразования около 800 мкВ/мТл. Они располагаются в латунной гильзе по окружности прутка под углом 120° друг относительно друга. В гильзе выфрезерованы канавки, в которые вклеиваются датчики так, что их чувствительные зоны максимально приближены к стержню. В гильзе закреплена оправка с отверстием под диаметр стержня, защищающая датчики от повреждения. Сигнал от каждого датчика, пропорциональный нормальной к поверхности стержня компоненте индукции магнитного поля, обрабатывается измерительным модулем, построенном по схеме прецизионного магнитометра [27], с чувствительностью не хуже 10 нТл/√Гц в полосе частот 0,1 – 10 Гц. Данные от модулей в цифровом виде поступают в блок цифровой обработки, который осуществляет синхронную работу модулей и передачу данных в персональный компьютер для дальнейшей обработки.
С помощью трехканального нанотеслометра проводилась магнитная дефектоскопия четырех прутков диаметром 3 мм и длиной 2 м из стали марки 65С2ВА. Гильза с датчиками закреплялась неподвижно, прутки равномерно протягивались через него со скоростью примерно 7,2 мм/с. Для обеспечения равномерного движения прутка его поверхность смазывалась машинным маслом. Во время исследования магнитограмма контролировалась на экране компьютера, и при возникновении подозрительного участка, он помечался краской. Металлографическая экспертиза, проведенная на предприятии ОАО «Северсталь-Метиз», показала наличие серии раковин с характерным размером до 0,04 мм на расстояниях 80 мм, 980 мм, 1000 мм и серии дефектов на расстоянии 1460 мм от начала прутка. В остальных прутках в отмеченных местах также были обнаружены раковины размером от 0,015 мм до 0,03 мм.
На магнитограммах, кроме полезного сигнала, присутствует шумовая составляющая. Оценка ее спектральной плотности мощности, произведенная по 100 отсчетам, равна 2 мкТл /√ Гц в полосе частот 1 – 6 Гц, что на два порядка выше собственных шумов нанотеслометра, то есть этот шум в основном определяется микроструктурой металла.
Совпадение результатов магнитографии естественных дефектов с результатами металлографического контроля подтверждает высокую разрешающую способность предложенного индикатора (1), который может использоваться для построения обучающих образов при проектировании экспертных систем, позволяющих разрешать дефекты с характерным размером менее 0,015 мм в деталях, которые не нужно дополнительно намагничивать.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы (государственный контракт 14.740.11.0830).
Литература
1.Загидулин Р.В., Дударев М.С., Щербинин В.Е. Определение параметров искусственных и естественных поверхностных дефектов в ферромагнитных изделиях // Дефектоскопия. – 1994. – № 2. – С. 38 – 46.
2.Щур М.Л., Загидулин Р.В., Щербинин В.Е. Самосогласованный расчет магнитостатического поля поверхностного дефекта. // Дефектоскопия. – 1988. – № 10. – С. 3 – 13.
3.Золотовицкий А.Б., Щур М.Л., Загидулин Р.В. Влияние нелинейной ферромагнитной среды на формирование магнитного поля внутреннего дефекта. // Дефектоскопия. – 1989. – № 5. – С. 42 – 50.
4.Новикова И.А. Математическая модель, количественно описывающая магнитостатические поля поверхностных дефектов, и ее применение в задачах дефектометрии // Дефектоскопия. – 1986. – № 2. – С. 37 – 45.
5.Загидулин Р. В., Щербинин В. Е. Определение геометрических параметров дефектов сплошности методами теории распознавания. Детерминированные признаки классификации // Дефектоскопия. – 1994. – № 12. – С. 70 – 83.
6.Хватов Л. А., Колтовой Н. А., Жукова Г.А. О применении методов распознавания образов для автоматизации магнитного контроля труб // Дефектоскопия. – 1986. – № 3. С. 55 – 60.
7.Загидулин Р.В., Мужицкий В.Ф., Курозаев В.П. О разрешении дефектов сплошности по топографии магнитного поля // Дефектоскопия. – 2000. – № 5. – С. 46 – 56
8.Шлеенков А.С., Мельник Р.С., Кротов Л.Н., Щербинин В.Е. Анализ возможностей метода восстановления магнитного поля применительно к магнитной дефектоскопии. 1. Дефектоскопия. – 1991. – № 5. – С. 33 – 38.
9.Семенов В. Г., Дзария Г. М. Решение обратной задачи по определению дипольного магнитного момента // Метрология. – 1977. – № 12. – С. 29 – 34.
10.Семенов В. Г. Синтез сферических методов определения параметров источников магнитного поля внутреннего и внешнего происхождения // Измерительная техника. – 1990. – № 12. – С. 35 – 37.
11.Вонсовский С.В. Простейшие расчеты для задач магнитной дефектоскопии // ЖТФ. – 1938. – Т. 8. – вып. 16. – С. 1453 – 1467.
12.Дремин И. М., Иванов О. В., Нечитайло В. А. Вейвлеты и их использование // Успехи физических наук – 2001. – Т. 171. – № 5. – С. 465 – 501.
13.Загидулин Р. В., Щербинин В.Е. Качество и информативность признаков классификации дефектов сплошности. Количество информации о параметрах дефектов // Дефектоскопия. – 1994. – № 12. – С. 55 – 60.
14.Загидулин Р. В. К расчету признаков классификации дефектов сплошности конечной протяженности в ферромагнитных изделиях // Дефектоскопия. – 1995. – № 10. – С. 50 – 58.
15.Кулеев В.Г., Лопатин В.В. О связи тангенциальной составляющей поля рассеяния с упругим изгибом ферромагнитной трубы // ЖТФ – 2000. – Т. 73. – Вып. 12. – с. 39 – 44.
16.Загидулин Р.В. Некоторые особенности топографии магнитных полей дефектов сплошности // Дефектоскопия. – 1995. – № 9. – С. 55 – 62.
17.Баштанов М.Е., Курбатов Н.В., Немцов М.В., Петровский А.Н. Канатный дефектоскоп // Научная сессия МИФИ-99. – Т. 9. – М.: МИФИ, 1999. – С. 41 – 44.
18.Сапожников А.Б., Мирошин Н.В. К вопросу о роли магнитной нелинейности среды при формировании поля скрытого дефекта // Труды ИФМ АН СССР – 1967. – Вып. 26. – С. 189 – 198.
19.Печенков А. Н., Щербинин В. Е. Некоторые прямые и обратные задачи технической магнитостатики – Екатеринбург: УрО РАН, 2004. – 177 с.
20.Янус Р. И. Некоторые расчеты по магнитной дефектоскопии // ЖТФ. – 1938. – Т. 8. – № 4. – С. 307 – 315.
21.Сапожников А.Б. Поля рассеяния от скрытых дефектов с малым раскрытием // Труды СФТИ. – 1948. – Вып. 26. – С. 189 – 193.
22.Гусев А.П. Магнитное поле двух взаимодействующих включений // Дефектоскопия. — 1992. — № 12. — C 25 – 28.
23.Волков Б. И. Оценка точности измерений полей дефектов датчиками Холла // Дефектоскопия. – 1976. – № 6. – С. 57 – 66.
24.Кобус А., Тушинский Я. Датчики Холла и магниторезисторы. – М.: Энергия, 1971. – 352 с.
25.Игнатьев В. К., Протопопов А. Г. Повышение разрешающей способности магнитометра на основе эффекта Холла // Известия ВУЗов. Приборостроение. – 2003. – Т. 46. – № 3. – С. 38 – 44.
26.Пат. 2311655 Российская Федерация. Способ уменьшения погрешностей Холловского магнитометра / Игнатьев В. К.; опубл. 27.11.2007.
27.Голубев А.А., Игнатьев В.К., Никитин А.В. Прецизионный магнитометр. Приборы и техника эксперимента. – 2008. – № 5. С. 123 – 128.