О запасе прочности и оценке надежности узлов металлоконструкций
Аннотация
Предлагается стохастическая модель оценки механических характеристик прочности на основе анализа функции надежности. Коррелируется связь функции надежности с нормативным коэффициентом запаса прочности. Даются рекомендации по назначению механических характеристик прочности по гауссовскому уровню и коэффициентам вариации. Предлагается аналитическая и графическая зависимость для оптимального назначения параметров надежности узлов металлоизделий по проведенным прочностным исследованиям.
Ключевые слова: Прочность, надежность, коэффициент запаса, механические характеристики, вероятностный анализ.Ключевые слова:
Из практики работоспособности узлов металлоконструкций известно, что распределение усилия (напряжения), а также распределение прочности всей конструкции подчиняются нормальному закону распределения с соответствующими плотностями вероятности [1,2]. Целью расчета надежности является определение критического напряжения, при котором запас прочности оказывается наименьшим. Пусть распределение усилия подчиняется нормальному закону с плотностью вероятности f1(x), математическим ожиданием m1 усилия (напряжения) и средним квадратическим отклонением σ1. Распределение прочности подчиняется нормальному закону с плотностью вероятности f2(x), математическим ожиданием прочности m2 и средним квадратическим отклонением σ2.
Графически распределение плотностей вероятности показано на рисунке 3.
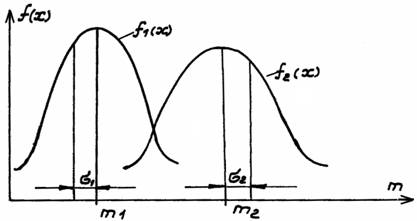
Рис. 1. Распределение плотностей вероятностей напряжений и усилий в узле.
Функция надежности такой системы определяется выражением вида [3]
![]() ,
,
где ![]() - нормированная нормальная функция распределения.
- нормированная нормальная функция распределения.
Практически функция надежности в проектных расчетах определяется, исходя из величины запаса прочности, т.е.
![]() ,
,
где n- коэффициент запаса прочности.
Расчет надежности узлов проводится для самых критических сечений, где запас прочности минимальный, а затем надежность узла находится как произведение надежности критических сечений, т.е. как последовательная схема соединений. Из практики известно, что при коэффициенте запаса прочности n≥1,4 надежность узла близка к единице: ![]()
Выберем нормативный коэффициент запаса прочности. Назначение нормативного коэффициента Кнорм запаса прочности является весьма сложной задачей, решение которой в настоящее время представляется возможным лишь в некоторых частных случаях нагружения.
Пусть выборка из опытных образцов изделия наблюдалась в эксплуатации достаточно длительное время Т, определяемое как функция точности и достоверности результатов эксперимента. При этом удалось установить:
M(Rmin)n- значение нижней границы доверительного интервала минимального параметра прочности;
M(σmax)в- значение верхней границы доверительного интервала максимальной нагрузки.
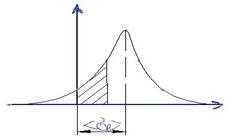
За эти значения можно принять, например предел прочности или предел текучести материала, выбираемые из нормативных документов или с использованием зисунка 2 . Тогда нормативный коэффициент запаса приближенно рассчитывается по формуле
![]()
Р
 σв
σв
Рис.2. Функция распределения механических характеристик материалов.
Если условия нагружения и внутреннего состояния конструкции позволяют принять исходные гипотезы, то решение удается привести к виду, более удобному для практического использования
![]()
где![]() ,
, ![]() - коэффициенты вариации параметра прочности и нагрузки, соответственно; μ- гауссовский уровень надежности [3].
- коэффициенты вариации параметра прочности и нагрузки, соответственно; μ- гауссовский уровень надежности [3].
В частном случае такого нагружения, когда σ=‹σ›- детерминированная величина,
![]()
Поэтому вероятность Q отказа будет равняться вероятности события противоположного, то есть
![]()
или с учетом первой гипотезы (о нормальном распределении)
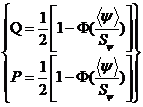
В соответствии с другой исходной гипотезой и теоремами теории вероятностей находятся параметры распределения

где ![]() - средние значения параметров прочности и нагрузки;
- средние значения параметров прочности и нагрузки; ![]() - дисперсии параметров прочности и нагрузки.
- дисперсии параметров прочности и нагрузки.
Отношение ![]() называется характеристикой безопасности или гауссовским уровнем надежности. Это понятие оказывается весьма удобным при пользовании таблицей значений функции Лапласа φ2 [3] , так как вероятность безотказной работы (неразрушения) составит
называется характеристикой безопасности или гауссовским уровнем надежности. Это понятие оказывается весьма удобным при пользовании таблицей значений функции Лапласа φ2 [3] , так как вероятность безотказной работы (неразрушения) составит
Р=φ2(μ)
и находится в этом случае непосредственно по таблице.
Наряду с вероятностным анализом оценивается и надежность аналогов и (или) конструктивных исполнений изделия. Если она не отвечает регламентированным требованиям, то устанавливают причины недостаточной надежности и рассматривают возможные мероприятия по ее повышению [2]. Для этого определяют достигнутый уровень надежности P, а также затраты С и полезный эффект E в стоимостном выражении. Наилучшим является такое решение Ропт, которое соответствует максимальному значению разности между Е и С (рисунок 3) , т. е.
Ропт![]()
или когда величина С достигает предельно допустимого значения.
Когда имеется большое число вариантов изделия, то каждый вариант изделия изображается на графике (рисунок 4) в виде точек с координатами Pи С. Линия, огибающая множества слева и сверху , проходит через наиболее предпочтительные варианты, соответствующие определенной стоимости. Остальные варианты заведомо хуже и их рассмотрение нецелесообразно.

Литература:
1.Труханов В. М. Надежность мобильных автоматических установок.- Волгоград: Волгоградский политехнический институт, 1989.
2.Кубарев А.И. Надежность в машиностроении.-М. : Издательство стандартов, 1989.-224 с.
3.Гмурман В.Е. Теория вероятностей и математическая статистика - М., Высш.шк., 2003.-479 с.