Математическая модель кадровой пирамиды бандподполья на Северном Кавказе
Аннотация
Математическая модель формализует решение задачи оптимального управления и имеет смысл минимизации численности региональной экстремистской системы (бандподполья) с учетом относительной важности составляющих ее частей при ограничениях, обусловленных «волей» государства к борьбе с экстремизмом и объективной динамикой численности групп экстремистов, определяемой факторами этносоциокультурной протестности (протестным потенциалом общества). Задача решалась с помощью имитационного моделирования по методу сценариев.
Ключевые слова: Математическая модель, метод сценариев, экстремизм, динамика численности групп экстремистов, проблемный регион, Северный Кавказ.Ключевые слова:
05.13.18 - Математическое моделирование, численные методы и комплексы программ
В настоящее время необходимым условием результативности исследовательской работы в области террористической деятельности на Северном Кавказе представляется широкое применение имитационных подходов, разнообразного моделирования, соединяющего социальные и математические методы. Именно моделирование позволяет, не ограничиваясь анализом сложившейся ситуацией, изучать возможные сценарии развития сложных социальных систем на короткую и более отдаленную перспективу [1-3].
На изложенной выше концептуальной основе была построена и исследована в режиме компьютерной имитации математическая модель, параметры которой идентифицированы на фактических показателях и экспертных оценках по Дагестану и Чечне [2,3]. Основу модели составляют балансовые соотношения, описывающие динамику численности различных групп-слоев двух крупнейших на Северном Кавказе республиканских ТП (Дагестана и Чечни) с учетом наличествующих и потенциально возможных действий государства по борьбе с экстремизмом [4,5].
Перед тем, как приступить к описанию построенной модели укажем, что любые количественные оценки размера отдельных групп-ступенек кадровой пирамиды ТП, в пределах всего Северного Кавказа или отдельных его республик по необходимости носят сугубо приблизительный характер. Даже самые информированные специалисты фиксируют скорее общий порядок данных образований, нежели их точную величину.
Как результат, количественные оценки северокавказских НВФ, располагаются в весьма широком диапазоне, который – не только свидетельство отсутствия у экспертного сообщества, силовиков или чиновников полной информации о количестве боевиков, но, в не меньшей степени, констатация того, что подобной «точной» цифры просто не существует. Речь идет о непрерывно пульсирующей величине, способной в зависимости от многих факторов в разы менять свой количественный формат в течении достаточно ограниченного времени. Менее динамичными во времени, но и менее поддающимися даже приблизительной количественной оценке являются группы пособников и сочувствующих бандподполью. В такой ситуации корректнее называть не конкретные цифры, но фиксировать именно диапазон, заключающий в своих пределах анализируемую социальную группу. Однако выставление вместо точного числа количественного диапазона было способно самым существенным способом осложнить построение «работающей» математической модели, сделав ее инструментальный аппарат слишком громоздким. Взвесив все «за» и «против», мы посчитали возможным упростить математическую часть, обозначив размер различных групп-прослоек кадровой пирамиды бандподполья точными цифрами (в качестве таковых были взяты примерные центры количественных диапазонов, фиксирующих края данных пульсирующих социальных образований).
Опишем построенную модель.
Балансовые соотношения:
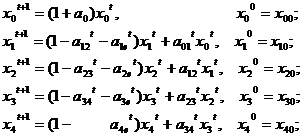(1)
где 
- численность i–й группы в году t (i=0 – население в целом; i=1 – среда психологического сочувствия бандподполья и пассивной эмоциональной поддержки; i=2 - среда соучастия, пассивного или активного пособничества ТП; i=3 – группа боевиков (республиканские НВФ); i=4 – организационное ядро бандподполья, группа лидеров, направляющих и регулирующих деятельность бандподполья;
- коэффициент перехода из группы i в группу i+1 за год t;
- коэффициент условно-безвозвратных потерь численности группы i в году t;
- численности групп в базовом году t=0, i=0,1,2,3,4; t=0,1,…,T-1.
Модельные гипотезы:
, (2)
- значение k-го фактора социальной протестности в году t (в баллах от 0 до 4);
k=1 – этносепаратизм; k=2 – материальная нужда; k=3 – стремление к наживе; k=4 – трансформированное (как правило, в религиозную форму) социальное «левачество»; k=5 – личностная мотивация (униженное достоинство, кровная месть и т.п.); k=6 – этносоциокультурный традиционализм; k=7 – исламский радикализм, представленный как последователями чистого ислама – салафитами/ваххабитами, так и фанатиками традиционного ислама;
- относительный вес фактора протестности k, 
Величина 
характеризует «протестный потенциал» общества в году t, который считается причиной движения снизу вверх по группам-слоям кадровой пирамиды бандподполья; 
- коэффициент пересчета суммарного взвешенного «протестного потенциала» в долю перехода из группы i в группу i+1 за год. Будем считать, что максимальная доля перехода составляет половину численности группы. Данное ограничение отражает известную консервативность социальных перемещений (в действительности доли перехода, как правило, в десятки раз меньше введенного нами ограничения); во-вторых, даже при максимальных значениях величин перехода и ухода из группы ее численность остается неотрицательной. Поскольку 
, то 
, где значения 
соответствуют полному отсутствию перехода и переходу половины состава i-й группы в (i+1)-ю. Далее,
(3)
- значение l-го способа борьбы с экстремизмом в году t (в баллах от 0 до 4); l=1 – ликвидация; l=2 – трансформация; l=3 – развитие и коррекция общества; l=4 – самокоррекция власти; l=5 – договор;
- относительный вес l-го способа борьбы с террористическим подпольем, 
Величина 
характеризует «потенциал борьбы с экстремизмом» в году t, который предполагается причиной сокращения численности региональной экстремистской системы; 
- коэффициент пересчета суммарного взвешенного потенциала борьбы с экстремизмом в долю ухода из группы i за пределы данной экстремистской системы за год. Аналогично предыдущему рассуждению будем считать, что максимальная доля возможного ухода составляет половину численности группы. Поскольку 
, то 
, где значения 
соответствуют полному отсутствию сокращения и уходу половины состава i-й группы.
С учетом гипотез (2) и (3) соотношения (1) можно переписать в виде
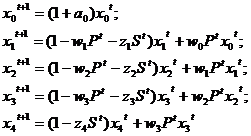(4)
с теми же начальными условиями. Помимо балансовых соотношений, вводится
Целевая функция (критерий оптимальности управления):
(5)
- коэффициент относительной важности сокращения численности группы i;
T – период рассмотрения.
Ограничения на управления:
(6)
- условный показатель желания/«воли» государства к борьбе с террористическим подпольем в году t 
.
Итак, задача оптимального управления (4)-(6) имеет смысл минимизации численности региональной экстремистской системы (бандподполья) с учетом относительной важности составляющих ее частей при ограничениях, обусловленных «волей» государства к борьбе с экстремизмом и объективной динамикой численности групп экстремистов, определяемой факторами этносоциокультурной протестности (протестным потенциалом общества). Задачу (4)-(6) целесообразно решать с помощью имитационного моделирования по методу сценариев [6].
Переменные состояния модели:
- численность i–й группы в t–м году, i=0,1,2,3,4;
Переменные управления:
- значение l–го способа борьбы государственной власти с экстремизмом в году t, l=1,2,3,4,5, t=1,…,T.
Модельные данные:
- начальные численности групп в базовом году t=0;
a0 – коэффициент естественного прироста населения данной республики;
- коэффициенты относительной важности сокращения численности отдельных групп-прослоек республиканского бандподполья;
{b1,…,b7} – относительные веса факторов социальной протестности;
{c1,…,c5} – относительные веса способов борьбы государства с террористическим подпольем;
{w0,…,w3} – коэффициенты пересчета суммарного взвешенного «протестного потенциала» в долю перехода из группы i в группу i+1 за год;
{z1,…,z4} - коэффициенты пересчета суммарного взвешенного потенциала борьбы с экстремизмом в долю ухода из группы i за пределы экстремистской системы (бандподполья) за год.
Указанные данные считаются постоянными и задаются экспертно.
- значения факторов социальной протестности на рассматриваемом периоде времени;
- значения показателя «воли» государства к борьбе с бандподпольем на рассматриваемом периоде времени.
Все эти последовательности данных задаются по сценариям.
Цель исследования:
решение задачи оптимального управления (4)-(6) с использованием имитационного моделирования.
Задачи исследования:
- получение сценариев моделирования отражающих различные варианты развития республиканских ТП на ближайшую и более отдаленную (среднесрочную) перспективу;
- идентификация модельных параметров в соответствии со сценариями;
- интерпретация полученных результатов и практические рекомендации по оптимизации борьбы с региональным террористическим подпольем.
- значения показателя «воли» государства к борьбе с экстремизмом на рассматриваемом периоде времени.
Литература:
1.Розин М.Д. Модельный подход к анализу и прогнозированию процессов социальных взаимодействий на Юге России // Инженерный вестник Дона, 2010. – №2. – Режим доступа: http://www.ivdon.ru/magazine/ latest/n2e2010/195/.
2.Розин М.Д., Сущий С.Я. Бандподполье Дагестана – моделирование динамики во втором десятилетии XXI века// Инженерный вестник Дона, 2011. – №3. – Режим доступа: http://www.ivdon.ru/magazine/ archive/n3y2011/562/.
3.Розин М.Д., Сущий С.Я. Реалии и перспективы Чеченской республики – экспертный анализ и моделирование ситуации// Инженерный вестник Дона, 2011. – №3. – Режим доступа: http://www.ivdon.ru/magazine/ archive/n3y2011/563/.
4.Розин М.Д., Сущий С.Я., Угольницкий Г.А. Методологические аспекты моделирования борьбы с коррупцией как фактором социальной конфликтности и терроризма // Научная мысль Кавказа. Междисциплинарные и специальные исследования. – 2011. - №2(18). – С.32-51.
5.Дьяченко В.К., Сивогривов А.А. Модель борьбы с экстремизмом в Дагестане. // Актуальные проблемы моделирования, проектирования и прогнозирования социальных и политических процессов в мультикультуральном пространстве современного общества: Материалы международной научн. конф. мол. ученых (г. Ростов-на-Дону, 18-19 апреля 2012 г.). – Р/Д: Изд-во СКНЦВШ ЮФУ, 2012. – 194 с. – С.52-55.
6.Лоу Аверилл М., Кельтон В. Дэвид. Имитационное моделирование. – СПб: Изд-во: Питер, BHV, 2004. – 848 с.