Модель равновесия подвижных элементов микромеханических зеркал с внутренними подвесами
Аннотация
Дата поступления статьи: 07.05.2013Разработана модель равновесия подвижных элементов микромеханических зеркал. Рассмотрены полученные результаты моделирования.
Ключевые слова: микросистемная техника, элементная база, модель, моделирование, зеркало
Одним из направлений развития микрооптикоэлектромеханических систем является разработка и исследование микромеханических зеркал (ММЗ). Данные микромеханические компоненты находят широкое применение как в микросистемах управления оптическими потоками, так и в лазерных и оптических дальномерах, используемых в системах ориентации и навигации подвижных объектов по рельефу местности [1, 2].
В работах [3, 4] рассмотрены конструкции интегральных микромеханических зеркал с крестообразным [5] и интегрированным внутренними подвесами [6], соответственно.
Для отклонения зеркального элемента в предложенных микромеханических компонентах применяются электростатические приводы (ЭСП). Всем электростатическим приводам присущ эффект неконтролируемого электростатического притяжения [7-10]. Критерии, позволяющие определить условия наступления данного эффекта, могут быть получены из модели равновесия зеркального элемента.
Разработанная модель равновесия зеркальных элементов предложенных микромеханических компонентов может быть представлено в нормированном виде:
![]() , (1)
, (1)
где W, n, U* – безразмерные переменные, определяемые выражениями:
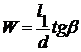 ; (2)
; (2)
![]() ; (3)
; (3)
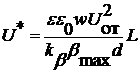 , (4)
, (4)
где ε – относительная диэлектрическая проницаемость воздушного зазора; ε0 – электрическая постоянная; l1, l2 – расстояния от оси вращения до краев неподвижных электродов электростатических приводов; w – ширина неподвижных электродов; d – расстояние между неподвижными электродами электростатических приводов и зеркальным элементом; β, βmax – угол и максимальный угол отклонения зеркального элемента; kβ – коэффициент жесткости упругого подвеса зеркального элемента; Uот – отклоняющее напряжение; L – длина зеркального элемента.
На рис. 1 представлена зависимость относительного смещения зеркального элемента W от приведенного напряжения U* при изменении относительного размера n неподвижных электродов электростатических приводов.
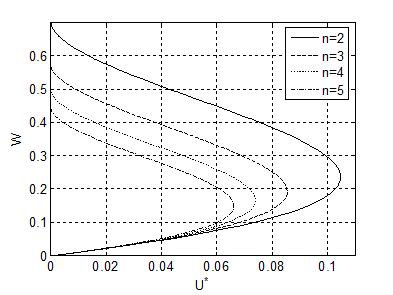
Рис. 1. Зависимость относительного смещения зеркального элемента W от приведенного напряжения U*
Кривые на рис. 1 отражают поведение зеркального элемента ММЗ при изменении управляющих напряжений на электростатических приводах. Оптимумы кривых определяют два состояния системы: нижняя ветвь соответствует устойчивому состоянию системы, а верхняя – неустойчивому. В неустойчивом состоянии системы малейшее изменение управляющих напряжений приводит к наступлению эффекта неконтролируемого электростатического притяжения и, соответственно, поломки устройства. Таким образом, работа электростатических приводов ММЗ должна выполняться в нижней части кривых. На расположение оптимума также влияет конфигурация электростатических приводов, в частности размеры неподвижных электродов ЭСП.
На рис. 2 и 3 представлены зависимости критических значений относительного смещения зеркального элемента W и приведенного напряжения U* определяющих наступление эффекта неконтролируемого электростатического притяжения от относительного размера неподвижных электродов n.
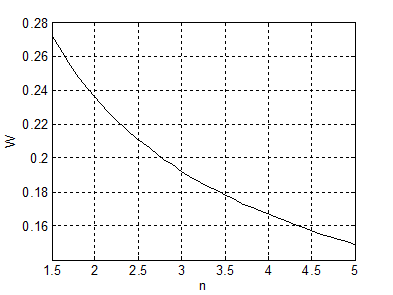
Рис. 2. Зависимость относительного смещения зеркального элемента W от относительного размера неподвижных электродов n ЭСП
С использованием выражений (1)-(4) и рис. 2, 3 можно определить максимальное значение отклоняющего напряжения приводящего к наступлению эффекта неконтролируемого электростатического притяжения при движении зеркального элемента (например, при n=2):
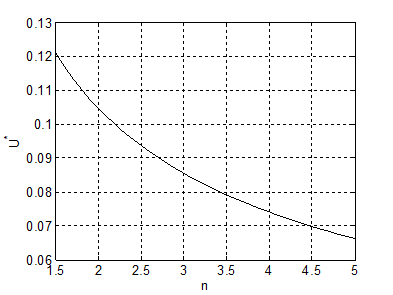
Рис. 3. Зависимость приведенного напряжения U* от относительного размера неподвижных электродов n электростатических приводов
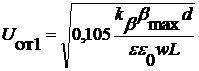 ; (5)
; (5)
 . (6)
. (6)
Однако, выражение (5) позволяет определить только максимальное значение постоянного отклоняющего напряжения Uот1. При подачи отклоняющего напряжения, изменяющегося по определенному гармонического закону, максимальное значение Uот2, приводящее к наступлению неконтролируемого электростатического притяжения, будет больше чем Uот1. Это связано с влиянием коэффициента электростатической упругости, создаваемого электростатическими актюаторами. В этом случае выражение для определения максимального значения отклоняющего напряжения при котором наступает эффект неконтролируемого электростатического притяжения примет следующий вид:
 . (7)
. (7)
Разработанная модель равновесия зеркальных элементов и полученные результаты моделирования могут использоваться при проектировании микромеханических зеркал с внутренними подвесами.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (шифр проекта «8.5757.2011»).
Литература:
- Berkeley sensor & actuator center [Электронный ресурс].– Режим доступа: http://www-bsac.eecs.berkeley.edu.
- Zhou, L. Optical MEMS for free-space communication [Text] / L. Zhou.– University of California, Berkeley, 2004.– 140p.
- Коноплев, Б.Г. Моделирование микрозеркала с электростатической активацией / Б.Г. Коноплев, И.Е. Лысенко // Микросистемная техника, 2002, №12.– С.22-25.
- Лысенко, И.Е. Моделирование интегрированного внутреннего упругого подвеса микромеханического устройства [Электронный ресурс] // Инженерный вестник Дона, 2010, №3. – Режим доступа: http://ivdon.ru/magazine/ (доступ свободный) – Загл. с экрана.– Яз. рус.
- Пат. 2265871 РФ, МКИ7 G 02 B 5/08, 26/08. Интегральное микромеханическое зеркало [Текст] / И.Е. Лысенко (Рос. Федерация) – № 2004117284/28; Заяв. 07.06.2004; Опубл. 10.12.2005, Бюл. № 34; Приоритет 07.06.2004. – 10 с.: ил. УДК 621.3.049.77.
- Пат. 2277255 РФ, МКИ7 G 02 B 26/08. Интегральное микромеханическое зеркало [Текст] / Б.Г. Коноплев (Рос. Федерация), И.Е. Лысенко (Рос. Федерация) – № 2005108758/28; Заяв. 28.03.2005; Опубл. 27.05.2006, Бюл. № 15; Приоритет 28.03.2005. – 10 с.: ил. УДК 621.3.049.77.
- Распопов, В.Я. Микромеханические приборы [Текст]: учебное пособие / В.Я. Распопов. – Тула: Тульский государственный университет, 2007. – 400 с.
- Лысенко, И.Е. Интегральный сенсор угловых скоростей и линейных ускорений [Электронный ресурс] // Инженерный вестник Дона, 2010, №3. – Режим доступа: http://ivdon.ru/magazine/ (доступ свободный) – Загл. с экрана.– Яз. рус.
- Лысенко, И.Е. Интегральные сенсоры угловых скоростей и линейных ускорений LR-типа на основе углеродных нанотрубок [Электронный ресурс] / И.Е. Лысенко, А.В. Лысенко // Инженерный вестник Дона, 2012, №4. – Режим доступа: http://ivdon.ru/magazine/ (доступ свободный) – Загл. с экрана.– Яз. рус.
- Лысенко, И.Е. Моделирование двухосевого микромеханического сенсора угловых скоростей и линейных ускорений LR-типа [Электронный ресурс] / И.Е. Лысенко // Инженерный вестник Дона, 2013, №1. – Режим доступа: http://ivdon.ru/magazine/ (доступ свободный) – Загл. с экрана.– Яз. рус.