Диагностика пьезокерамического элемента по активной составляющей проводимости

Аннотация

В.Л. Земляков, С.А. Толмачев

Дата поступления статьи: 05.04.2013

Получена оценка шага дискретизации по частоте при решении задач диагностики пьезокерамического элемента разными методами по измерениям активной составляющей проводимости в ряде дискретных точек. Это позволит не потерять в точности и, в то же время, сократить объем измерений и количество вычислительных операций.

Ключевые слова: пьезокерамический элемент, добротность, активная составляющая проводимости

01.04.06 - Акустика

05.13.05 - Элементы и устройства вычислительной техники и систем управления

Активная составляющая проводимости пьезокерамического элемента (ПКЭ)  является одной из основных частотных характеристик, позволяющих проводить диагностику ПКЭ. Она может быть записана в виде [1]:
,   (1)
где  – активное сопротивление на частоте механического резонанса , ,  – механическая добротность.
Рассматриваемая частотная характеристика может измеряться в непрерывном режиме, когда на ПКЭ воздействует синусоидальный сигнал с линейно изменяющейся частотой. Визуально наблюдаемая, например, на экране индикатора амплитудно-частотных характеристик, непрерывная функция  позволяет качественно оценить свойства ПКЭ.
В последнее время получили распространение измерительно-вычислительные комплексы на базе персонального компьютера, в которых измерение частотной характеристики активной составляющей проводимости проводится в дискретных точках k значений  с шагом по частоте . При таких измерениях важно определить наибольшее значение , при котором сохраняется достаточная точность получения результата, реализуется минимально возможный объем измерений и вычислительных операций.
Различные методы определения параметров ПКЭ по частотной характеристике активной составляющей проводимости рассмотрены, например, в [2 – 6].
Предполагая, что в зависимости от цели исследований ПКЭ, значение шага дискретизации может быть различным, рассмотрим определение  для трех измерительных задач:

1. Восстановление непрерывной частотной зависимости активной составляющей проводимости по последовательности отсчетов (в соответствии с теоремой В.А. Котельникова) [7, 8];
2. Определение добротности ПКЭ и пьезомодуля материала через интеграл от активной составляющей проводимости (площадь под кривой) [9];
3. Определение добротности ПКЭ и пьезомодуля материала по максимальному значению производной от активной составляющей проводимости [10 – 12].

Для решения первой задачи выполним следующие операции.
Преобразуем  к виду  и, используя обозначение , для  получим
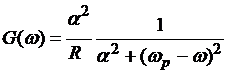.        (2)
Используя симметрию преобразования Фурье относительно переменных  и [7], для максимального шага дискретизации получим , где  – длительность сигнала , формирующего спектральную функцию .
Преобразование Фурье для функции , представленной в виде (2), имеет вид
.
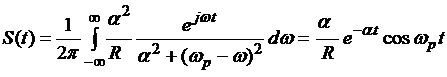Потребуем выполнения равенства [8], тогда
.
Учитывая, что , где  – ширина резонансной кривой активной составляющей проводимости на уровне 0,5 от максимального значения, получим, .
Учитывая рекомендацию выбирать  в три – четыре раза меньше максимального значения, рекомендуемое число точек N в диапазоне значений, равном ширине резонансной кривой должно быть N = 10, или
.    (3)
Для решения второй задачи определим добротность через интеграл от активной составляющей проводимости.
Для вычисления интеграла , воспользуемся результатами работы [9], в которой соотношение (1) представлено в виде

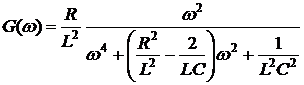
Тогда, используя обозначения

,
запишем

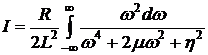
После применения теоремы о вычетах получим

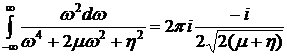
Подставляя значения  и , в итоге получим
.    (4)
Воспользуемся известной из электротехники связью динамической индуктивности с добротностью. Тогда
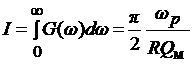.      (5)
Для решения третьей задачи воспользуемся тем, что график активной составляющей проводимости имеет точку перегиба, соответствующую частоте максимума производной от активной составляющей проводимости по частоте , как это сделано в работах [10 – 12]. Выполним дифференцирование выражения (1):

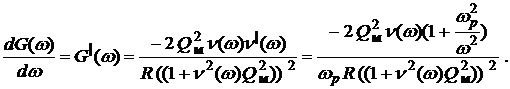
Выполним некоторые преобразования, опираясь на формулу (1).
Введем обозначение
,
где  соответствует частоте, на которой активная составляющая проводимости равна половине максимального значения.
Определим вторую производную от функции вида  и приравняем ее к нулю. В результате получим
.
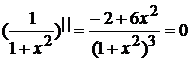Из последнего выражения следует, что , следовательно, получаем
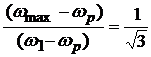.   (6)
Значение производной на частоте максимума, с учетом равенства (6), определяется по формуле


В итоге получим
.        (7)
Для проведения исследования трех рассмотренных измерительных задач с использованием среды программирования Matlab были разработаны соответствующие приложения.
В результате компьютерного эксперимента для эквивалентной электрической схемы ПКЭ с исходной добротностью  были получены результаты, представленные на рис. 1 а, б:  рис. 1 а соответствует погрешности определения добротности по формуле (4), а рис. 1 б – определения добротности по формуле (7).
Погрешность определения величины добротности в зависимости от числа точек N в диапазоне значений, равном ширине резонансной кривой активной составляющей проводимости рассчитывалась по формуле

Поскольку при определении добротности путем интегрирования результат зависит от расположения точек измерения, на рис. 1 а приведены наибольшие значения погрешности при фиксированном N.

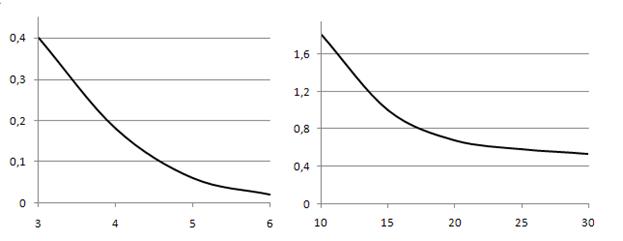
Рис. 1. Зависимость погрешности определения добротности от числа точек в диапазоне значений, равном ширине резонансной кривой

Из представленного материала следует, что, в зависимости от цели исследований ПКЭ, количество точек измерения активной составляющей проводимости (значение шага дискретизации) может быть различным:

• для восстановления непрерывной частотной зависимости активной составляющей проводимости по последовательности отсчетов (в соответствии с теоремой В.А. Котельникова) необходимо иметь шаг дискретизации по частоте соответствующий наличию примерно 10 точек в диапазоне значений, равном ширине резонансной кривой активной составляющей проводимости;
• для определения добротности ПКЭ через интеграл от активной составляющей проводимости (площадь под кривой) необходимое количество точек измерения в том же диапазоне не менее 5 – 6;
• для определения добротности ПКЭ по максимальному значению производной от активной составляющей проводимости количество точек в диапазоне значений, равном ширине резонансной кривой активной составляющей проводимости составляет не менее 15 – 20.

Работа выполнена на оборудовании ЦКП «Высокие технологии» ЮФУ при финансовой поддержке Минобрнауки России в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы».

Литература:

1. Пезокерамические преобразователи: Справочник. / Под ред. С.И.Пугачева. Л.: Судостроение, 1984. – 256 с.
2. Акопьян В. А., Соловьев А. Н., Шевцов С. Н. Методы и алгоритм определения полного набора совместимых материальных констант пьезокерамических материалов. Ростов н/Д: Изд-во ЮФУ, 2008. 144 с.
3. Земляков В. Л.  Методы и средства измерений в пьезоэлектрическом приборостроении: монография. Ростов н/Д: Изд-во ЮФУ, 2009. 180 с. (Пьезоэлектрическое приборостроение. Т. 5).
4. V.L. Zemlyakov Methods for Determination of the Piezoelectric Coefficient of Piezoceramic Materials in Terms of Parameters of an Equivalent Circuit of a Piezoelement // Piezoelectrics and Related Materials: Investigations and Applications. Pub. Date: 2012 2nd Quarter, р. 117-142.
5. Zemlyakov V.V., Zemlyakov V.L. A new approach to measuring the piezomodulus of a piezoceramic material under dynamic conditions // Measurement Techniques. 2002. V. 45. N 4. P. 421.
6. Земляков В. Л. Измерение пьезомодуля по активной составляющей проводимости пьезокерамического элемента // Измерительная техника. 2009. № 8. С. 64–66.
7. Радиотехнические цепи и сигналы. / Под ред. К.А. Самойло. М.: Радио и связь, 1982. – 528 с.
8. Земляков В. Л. О дискретности записи частотной характеристики проводимости пьезоэлементов // Сборник трудов Междунар. научно-практич. конф. «Актуальные проблемы пьезоэлектрического приборостроения». Ростов н/Д: Изд-во ООО «ЦВВР», 2006. С. 160–162.
9. Патент РФ 1648175 МПК H03H 3/02. Способ определения пьезомодулей / В. Л. Земляков – Опубл. 28.02.1994. Бюл. № 8.
10. Земляков В. Л., Ключников С. Н. Определение параметров пьезокерамических элементов по амплитудным измерениям // Измерительная техника. 2010. № 3. С. 38–40.
11. Ключников С.Н. Метод определения добротности резонансных систем по амплитудным измерениям и его аппаратная реализация на базе LABVIEW [Электронный ресурс] // Инженерный вестник Дона.  2011. №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4y2011/521.
12. Земляков В. Л., Ключников С. Н.Определение пьезомодуля материала пьезокерамического элемента. [Электронный ресурс]. Инженерный вестник Дона. 2012. № 2. – Режим доступа:  (http://ivdon.ru/magazine/archive/n2y2012/803)