Планирование энергоэффективных траекторий полета стратосферного дирижабля-челнока многоуровневой транспортной системы МААТ

Аннотация

В.Х. Пшихопов, В.А. Крухмалев

Дата поступления статьи: 23.05.2013

Поставлена задача создания системы планирования энергоэффективных траекторий движения стратосферного дирижабля. Проанализированы возможности применения различных интеллектуальных подходов для решения задачи. Сделаны вывод о применение генетических алгоритмов. Проанализированы результаты работы генетических алгоритмов с различныи операторами.

Ключевые слова: МААТ, стратосферный дирижабль, система управления, планирование, генетические алгоритмы

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Экологически безопасная и экономически эффективная транспортировка грузов и пассажиров представляют большой интерес в наше время. Решение этих вопросов в классе стратосферных воздухоплавательных платформ осуществляется в рамках проекта Multibody Advanced Airship for Transport (МААТ), выполняемого под финансированием Еврокомиссии. Система МААТ состоит из двух основных структурных элементов – крейсера, осуществляющего безостановочный полет на высотах 14-16 км с грузом и пассажирами на борту [1]. Для доставки грузов и пассажиров из аэропорта на борт крейсера и обратно используется дирижабль-челнок. Он осуществляет преимущественно вертикальный полет в диапазонах высот от 0 до 16 км с максимальной вертикальной скоростью 5 м/с. Полет челнока ввиду ограниченности энергоресурсов на борту и высоких аэродинамических нагрузок является важным вопросом проектирования всей системы. Поэтому разработка энергоэффективных подходов планирования движения челнока является актуальной задачей ввиду предъявляемых заказчиком требований нулевого эмиссионного выброса и экономической эффективности функционирования. При этом следует заметить, что система планирования является стратегическим уровнем управления, тактический уровень обеспечивается позиционно-траекторным регулятором [2-6].
Предлагаемые подходы к разработке системы планирования основываются на данных Всемирной метеорологической организации [7]. В работах [8,9] предложена методика получения статистических моделей скорости и направления ветра в зависимости от времени года. Иллюстрация такой модели приведена на рис. 1. Она представляет собой математические ожидания скоростей ветра с математическим ожиданием направления находящегося в секторе 70-процентного доверительного интервала на соответствующих высотах.
Таким образом, поставлена задача построения энергетически эффективной траектории полета челнока для статистической модели среды, полученной из реально измеренных значениях ветровых нагрузок с учетом упрощающих допущений.
Для решения поставленной задачи был сделан выбор между нейросетями, системами на базе нечетких подходов и генетическими алгоритмами.
В таблице № 1 приведено сравнение их достоинств и недостатков [10].

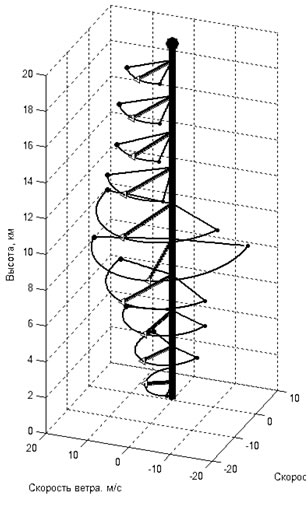
Рис. 1 – Статистическая модель ветра

Таблица № 1
Сравнение различных интеллектуальных подходов

Учитывая поставленную задачу, а также достоинства и недостатки приведенных в таблице № 1 подходов, принято решение использовать генетические алгоритмы.
Приняты следующие допущения:

• осуществляется управление только вертикальной скоростью всплывания, горизонтальное перемещение обеспечивается дрейфом в ветровом потоке;
• скорость дрейфующего дирижабля равна скорости ветра;
• направление движения дрейфующего дирижабля совпадает с направлением ветра;
• минимальное время присутствия в потоке обуславливается максимальной вертикальной скоростью 5 м/с;
• как только дирижабль выходит из одного потока, он попадает в другой, пока не достигнет целевой точки.

Для генетического алгоритма задача формализована следующим образом. Оптимизируемая алгоритмом функция: (1)
где – номер ветрового потока,   общее количество потоков, - время присутствия дирижабля в i-м ветровом потоке.
Так как время полета вдоль траектории пропорционально энергетическим затратам на стабилизацию дирижабля, упрощенно можно считать формулу (1) обеспечивающей энергетическую эффективность спланированной траектории.
Накладываем линейные ограничения. Так данные представлены дискретно для каждой высоты, то удобно интерпретировать задачу в двумерном виде. Тогда линейные ограничения в виде равенств, исходя из необходимости выхода в целевую точку  и принятых допущений, имеют вид: (2)
где  – номер ветрового потока,  общее количество потоков, отсчет идет от нижнего потоков к верхнему,  вектор математического ожидания скорости i-го потока, - математическое ожидание время присутствия дирижабля в i-м ветровом потоке. Т.к. модель рассматривается в двумерном случае, то вектор конечного положения состоит из двух элементов – абсциссы  и ординаты , вектор математического ожидания скорости также состоит из проекций математическое ожидание скорости на ось абсцисс и ось ординат , рассчитанных исходя из скалярного значения математического ожидания скорости ветра и математического ожидания его направления.

Также возможно применение квадратичного критерия качества в виде: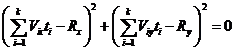 (3)
Хотя задача представлена в двумерном виде, реальность трехмерной задачи учитывается в виде минимального времени  прохождения дирижаблем i-го потока толщиной  в силу ограниченности максимальной скорости подъема дирижабля , т.е. (4)
Отсюда еще один класс ограничений в виде нижних границ имеет вид:

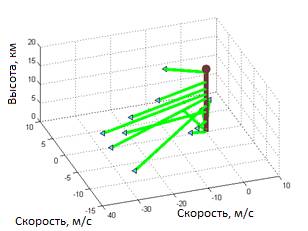
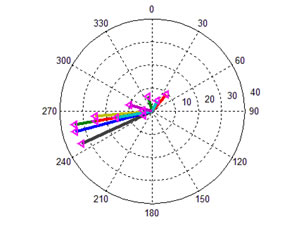
Так как получение статистических моделей предполагает значительные вычислительные и временные затраты, для испытания предлагаемой методики использованы данные в диапазоне высот 0-16 км 20 января 2011 года в г. Болонья, Италия. Диапазон высот разбит на 12 неодинаковых участков. Считаем, что на каждом участке скорость и направление ветра не меняются. Данные проиллюстрированы графиками на рисунке 2 и рисунке 3. На рис. 2 показаны скорости ветра с реальным направлением, по вертикальной оси отмечены высоты соответствующих ветровых потоков. На рис. 3 показана двумерная картина скоростей и направлений ветра на полярном графике.

R = (-60000 м, 20000 м) выбран случайно из эмпирической оценки диаграммы распределений ветра на рис. 3. Подставляя значения скоростей горизонтальных воздушных потоков в (2) получаем ограничения решаемой проблемы в виде уравнений: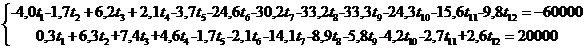

Ограничения в виде неравенств (5) рассчитаны исходя из  м/с:

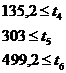
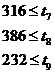
В работе представлены результаты трех экспериментов с разными операторами. Они приведены в таблице № 2. Причем эксперименты 3 отличаются от экспериментов 1 и 2 предъявление квадратичного критерия (3) вместо линейного (2).
Таблица № 2
Параметры генетических алгоритмов в различных экспериментах

Результаты работы алгоритмов приведены в таблице № 3 и на рис. 3-8.

Таблица № 3
Производительность алгоритма

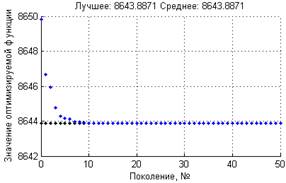
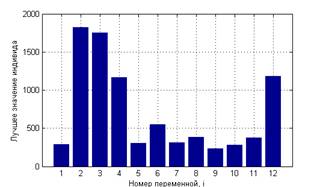
Рис. 3 – Результаты работы алгоритма в эксперименте 1

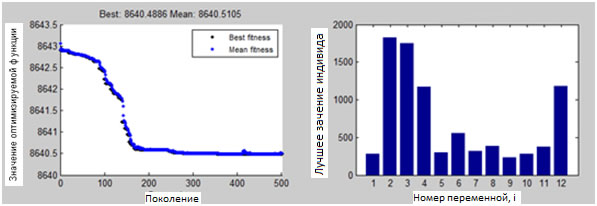
Рис. 4 – Результаты работы алгоритма в эксперименте 2

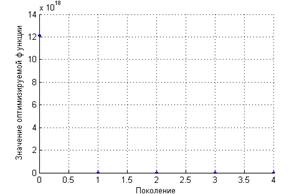
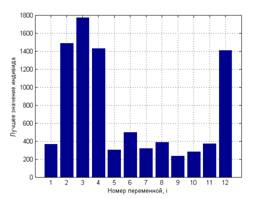
Рис. 5 – Результаты работы алгоритма в эксперименте 3

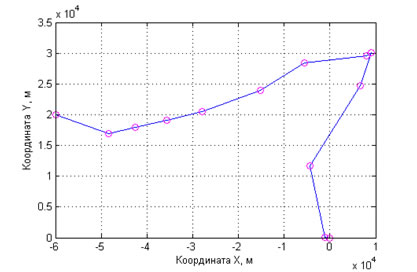
Рис. 6 – Полученная в эксперименте 1 траектория

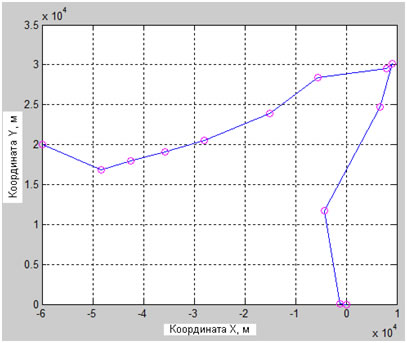
Рис. 7 – Полученная в эксперименте 2 траектория

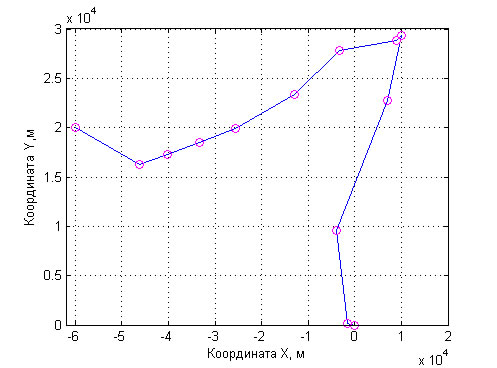
Рис. 8 – Полученная в эксперименте 3 траектория

Полученные результаты работы планировщика перемещений показывают незначительную разницу в результирующей оптимизированной траектории, в тоже время временные затраты различаются значительно. Сделан вывод о необходимости исследования возможности адаптивного подбора параметров операторов генетических алгоритмов.

Литература:

1. Dumas A., Trancossi M., Madonia M., Giuliani I. Multibody Advanced Airship for Transport [Electronic resource] // SAE Technical Paper, 2011. – №2011-01-2786, URL: http://papers.sae.org/2011-01-2786/ (paid access).
2. Федоренко, Р.В. Алгоритмы автопилота посадки роботизированного дирижабля [Электронный ресурс] // Электронный научно-инновационный журнал Инженерный вестник Дона, 2011. – №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2011/371 (доступ свободный).
3. Кульченко, А.Е. Структурно-алгоритмическая организация автопилота робота-вертолета [Электронный ресурс] // Электронный научный журнал Инженерный вестник Дона, 2011, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2011/330 (доступ свободный).
4. Пшихопов, В.Х. Проектирование систем управления роботизированных воздухоплавательных комплексов на базе дирижаблей / В.Х. Пшихопов, М.Ю. Медведев, М.Ю. Сиротенко, О.Э. Носко, А.С.  Юрченко // Известия ТРТУ. Тематический выпуск «Перспективные системы и задачи управления». – Таганрог, 2006. – № 3 (58). – С. 160–167.
5. Пшихопов В.Х. Структурный синтез автопилотов подвижных объектов с оцениванием возмущений / В.Х. Пшихопов, М.Ю. Медведев // – М.: Информационно-измерительные и управляющие системы, 2006. – №1. – С.103–109.
6. Пшихопов В.Х. Синтез адаптивных систем управления летательными аппаратами / В.Х. Пшихопов, М.Ю. Медведев // Известия Южного федерального университета. Технические науки, 2010. – Т. 104. – № 3. – С. 187-196.
7. National Oceanic and Atmospheric Administration, Integrated Global Radiosonde Archive [Electronic resource] // URL: ftp://ftp.ncdc.noaa.gov/pub/data/igra (free access).
8. Pshikhopov, V., Krukhmalev, V., Medvedev, M., Neydorf R. Estimation of Energy Potential for Control of Feeder of Novel Cruiser/Feeder MAAT System [Text] / SAE Technical Paper, 2012. – №2012-01-2099, URL: http://papers.sae.org/2012-01-2099/ (paid access).
9. Пшихопов, В.Х. Вероятностные подходы к оценке среды функционирования челнока многоуровневой транспортной системы на базе дирижаблей [текст доклада] / В.Х. Пшихопов, М.Ю. Медведев, Р.А. Нейдорф, В.А. Крухмалев // Материалы конференции «Информационные технологии в управлении», 2012, – С. 646-655.
10. Гладков, Л. А. Генетические алгоритмы [Текст]: Учебное пособие / Л. А. Гладков, В. В. Курейчик, В. М. Курейчик. – 2-е изд. – М: Физматлит, 2006. – С. 320. – ISBN 5-9221-0510-8