Статистический анализ выборок курсов валют с помощью ранговых критериев
Аннотация
Дата поступления статьи: 30.04.2013В статье анализируется возможность применения ранговых критериев для статистического анализа двух выборок. Рассматриваются критерии Вилкоксона, Ван дер Вардена и Манна-Уитни для проверки гипотезы о совпадении центральных тенденций сравниваемых выборок, критерий Сиджела-Тьюки для проверки гипотезы о равенстве размахов варьирования и критерий Колмогорова-Смирнова для проверки гипотезы о равенстве законов распределения. Анализ проводится на данных о курсах доллара США в различных банках.
Ключевые слова: статистика, ранг, выборка, гипотезы статистические, критическое значение, нормальное распределение, сопряжённые пары
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Одна из самых обычных задач в математической статистике – это задача о сравнении двух выборок. В отличие от обычных критериев [1,8], использование ранговых критериев не накладывает никаких ограничений на тип распределения случайной величины. В ранговых критериях можно различать три группы. Критерии первой группы проверяют гипотезу о совпадении центральных тенденций сравниваемых совокупностей, второй- гипотезу о равенстве размахов варьирования, третьей- гипотезу о равенстве законов распределения[1]. Нулевая гипотеза для критериев первой группы формулируется как H0: = , где и - характеристики центров распределения случайных величин и соответственно, реализациями которых являются выборочные значения x и y. Альтернативами будут: H1: ≠ ; H2: > ; H3: < .
Критерий Вилкоксона
Пусть имеются две выборки: x1, x2,… xm и y1, y2,… yn , причем их объёмы не обязательно должны быть одинаковыми. Объединим обе выборки в одну и упорядочим её. В качестве меры близости центральных тенденций двух выборок можно взять сумму рангов значений, принадлежащих каждой исходной выборке. Эта величина называется статистикой (критерием) Вилкоксона. Итак, имеем две величины:
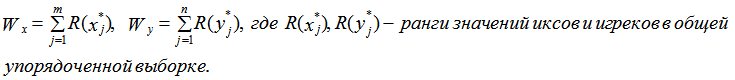
В том случае, если объёмы выборок одинаковы, с критическим значением сравнивается меньшая сумма рангов. Нулевая гипотеза отвергается, когда Wx(или Wy)<W() , где W()-критическое значение статистики Вилкоксона. Для выборок с неодинаковыми объёмами вычисляют “дополнение”[1,6].
В тех случаях, когда выборка образована значениями случайной величины с нормальным распределением, лучше воспользоваться более чувствительным критерием, а именно Х-критерием Ван дер Вардена[1,5].
Критерий Ван дер Вардена
Пусть имеются две выборки: x1, x2,… xm и y1, y2,… yn. Проделаем ту же процедуру, что и в случае критерия Вилкоксона. Разделим теперь ранги значений на N+1, где N=n+m, и вычислим сумму 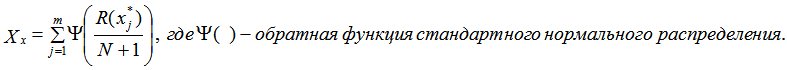 Значения Xx и Xy различаются лишь по знаку, поэтому удобнее рассчитывать статистику для выборки меньшего объёма. В зависимости от альтернативы нулевая гипотеза отвергается с уровнем значимости , если |X|>X() для альтернатив H2 и H3 и если |X|>X(2) для альтернативы H1.
Значения Xx и Xy различаются лишь по знаку, поэтому удобнее рассчитывать статистику для выборки меньшего объёма. В зависимости от альтернативы нулевая гипотеза отвергается с уровнем значимости , если |X|>X() для альтернатив H2 и H3 и если |X|>X(2) для альтернативы H1.
Критерий Манна-Уитни
Для проверки гипотезы сдвига Манн и Уитни предложили ранговый критерий, основанный на статистике [2]:
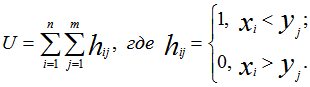
Если U1()≤U≤ U2(), гипотеза сдвига отклоняется (U1() и U2()- критические значения, берущиеся из таблицы).
Статистический анализ часто проводится в банковских операциях[7,9,10].
Рассмотрим примеры и применим ранговые критерии к сравнению двух выборок x и y-курсов валют за два соседних дня в девяти коммерческих банках. Были исследованы четыре базовых примера:
-
Курсы продажи доллара США за 17-18.12.2003. При этом курс
Центрального Банка России(ЦБ) уменьшился, значит следует ожидать отклонение гипотезы о равенстве центральных тенденций двух выборок.
-
Курсы продажи доллара за 25-26.12.2003. В эти два дня курс ЦБ не изменился, следовательно нужно ожидать подтверждение нулевой гипотезы.
-
Курсы покупки доллара за 17-18.12.2003.
-
Курсы покупки доллара за 25-26.12.2003.(См.таблицу)
| Курс доллара США к рублю. | ||||||||
| Банки | 17.12.2003 | 18.12.2003 | 25.12.2003 | 26.12.2003 | ||||
| Покупка | Продажа | Покупка | Продажа | Покупка | Продажа | Покупка | Продажа | |
| 1 | 28 | 29,7 | 27,7 | 29,3 | 28 | 29,27 | 28 | 29,25 |
| 2 | 28,8 | 29,48 | 28,8 | 29,4 | 28,2 | 29,28 | 28,7 | 29,3 |
| 3 | 28,1 | 29,57 | 28 | 29,3 | 27,5 | 29,29 | 27 | 29,27 |
| 4 | 29 | 29,4 | 28,7 | 29,3 | 28,1 | 29,23 | 27,9 | 29,4 |
| 5 | 28,2 | 29,32 | 28,3 | 29,3 | 28 | 29,25 | 28 | 29,26 |
| 6 | 29,1 | 29,59 | 28,3 | 29,3 | 28 | 29,39 | 28 | 29,59 |
| 7 | 28,9 | 29,3 | 28,7 | 29,25 | 28,9 | 29,28 | 28,9 | 29,25 |
| 8 | 29 | 29,6 | 28,5 | 29,35 | 27,5 | 29,2 | 27,5 | 29,1 |
| 9 | 28 | 29,37 | 27,7 | 29,3 | 28 | 29,27 | 28 | 29,25 |
| Курс ЦБ | 29,3 | 29,25 | 29,245 | 29,245 | ||||
Применение к примерам 1-4 критериев дало следующие результаты:
1) Меньшая сумма рангов W=53,5<W(), X=5,22> X(),U=8≤ U1() для всех . Нулевая гипотеза отвергается. 2) W=80>W(), X=0,631< X(),U1(()≤U=26≤ U2()для всех . Нулевая гипотеза не отвергается. 3) W=70,5>W(),X=2,79< X(),U1()≤U=24≤ U2()для всех . Нулевая гипотеза не отвергается.
4) W=80,5>W(),X=0,844< X((),U1()≤U=34≤ U2() для всех . Нулевая гипотеза не отвергается. Критические значения брались из таблиц [1,2].
Распределения могут отличаться не только средним значением, но и разбросом, в качестве меры которого обычно выступает дисперсия. Нулевая гипотеза для критериев второй группы формулируется так:
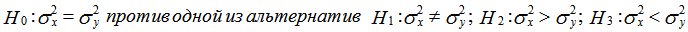
в предположении, что центры распределения практически совпадают.
Модификация Сиджела-Тьюки критерия Вилкоксона
Поступим с выборками x и y так же, как и в случае критерия Вилкоксона. Ранги после этого определим по правилу чередования [4]. Обозначим Sx и Sy суммы рангов для выборок x и y соответственно. Пусть S- меньшая из сумм Sx и Sy и S’=min(m,n)(N+1)-S. (Здесь N=n+m). Нулевая гипотеза отвергается , если S и S’ оказываются меньше критического значения W() для статистики Вилкоксона. Применение к примерам 1-4 критерия Сиджела-Тьюки дало следующие результаты:
1) Sx=75, Sy=96, S=75, S’=96> W() для всех . Нулевая гипотеза не отвергается. 2) Sx=98, Sy=73, S=73, S’=98> W() для всех . Нулевая гипотеза не отвергается. 3) Sx=67, Sy=104, S=67, S’=104> W() для всех . Нулевая гипотеза не отвергается. 4) Sx=89, Sy=82, S=82, S’=89> W() для всех . Нулевая гипотеза не отвергается.
Нулевая гипотеза для критериев третьей группы формулируется как
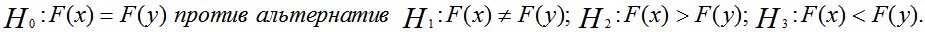
Критерий Колмогорова-Смирнова
Критерий основан на сравнении рядов накопленных частот обеих совокупностей. Пусть Fj(x) и Fj(y)- накопленные относительные частоты выборок x и y; где j- номер значения в общем вариационном ряду. Максимальная по величине разность 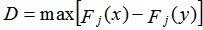 может служить мерой близости двух распределений. При больших объёмах совокупностей (m,n>100) если D больше критического значения D(), то нулевая гипотеза о равенстве распределений отвергается. Если объёмы совокупностей малы, приходится вводить поправки [3,6]. Применение к примерам 1-4 критерия Колмогорова-Смирнова дало везде ожидаемые результаты. Таким образом можно сделать следующий вывод после применения всех ранговых критериев: лишь для примера 3 все критерии первой группы дали неверный результат. Во всех остальных случаях все критерии подтвердили ожидания.
может служить мерой близости двух распределений. При больших объёмах совокупностей (m,n>100) если D больше критического значения D(), то нулевая гипотеза о равенстве распределений отвергается. Если объёмы совокупностей малы, приходится вводить поправки [3,6]. Применение к примерам 1-4 критерия Колмогорова-Смирнова дало везде ожидаемые результаты. Таким образом можно сделать следующий вывод после применения всех ранговых критериев: лишь для примера 3 все критерии первой группы дали неверный результат. Во всех остальных случаях все критерии подтвердили ожидания.
Литература
1. Благовещенский Ю.Н., Самсонова В.П., Дмитриев Е.А. Непараметрические методы в почвенных исследованиях. [Текст]: Монография/
2. Ю.Н.Благовещенский и др. - Москва: ”Наука”, 1987. – 98 с.
3. Кобзарь А.И. Прикладная математическая статистика. [Текст]: Монография/ А.И.Кобзарь - Москва: Физматлит, 2006, - 816 с.
4. Хеттманспергер Т. Статистические выводы,основанные на рангах. [Текст]: Монография/ Т.Хеттманспергер - Москва:”Финансы и статистика”, 1987, - 333 с.
5. Орлов А.И. Эконометрика. [Текст]: Монография/А.И.Орлов - Москва: Экзамен, 2006, - 576 с.
6. Gibbons J. D., Chakraborti S. Nonparametric Statistical Inference, 4th Ed. — CRC, 2003 — 608 с. Hajek J., Sidak Z., Sen K. P. Theory of rank tests(second edition). — Academic Press, 1999. - 450 p.
7. Пучков Е.В. Разработка системы поддержки принятия решений для управления кредитными рисками банка. [Электронный ресурс]// «Инженерный вестник Дона», 2011, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2011/377 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Галушка В.В., Фатхи В.А. Формирование обучающей выборки при использовании искусственных нейронных сетей в задачах поиска ошибок баз данных. [Электронный ресурс] // «Инженерный вестник Дона», 2013, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1597 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Волосатова Т.А. Явление агрессивной скупки акций на российском финансовом рынке. [Текст] // Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно-практической конференции ППС и молодых учёных / Рост. гос. экон. ун-т “РИНХ”-Ростов н/Д., 2009. – С.142-146.
10. Данекянц А.Г. Различные модели осуществления скупки акций. [Текст] // Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно-практической конференции ППС и молодых учёных / Рост.гос.экон.ун-т “РИНХ”-Ростов н/Д., 2009. – С.146-149.