Вывод соотношений сопряжения при расчете блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки
Аннотация
Дата поступления статьи: 30.04.2013Статья посвящена прочностным расчетам составных конструкций. Рассмотрен вывод разрешающей системы уравнений определения напряженно-деформированного состояния конструкции, состоящей из основания в форме шестиугольной пластины, жестко связанной с основанием круговой цилиндрической оболочки.
Ключевые слова: пластина, оболочка, прочность, составная конструкция.
В большинстве конструкций применяются сложные составные детали. Стремление получить конструкцию наиболее легкой и, вместе с тем, максимально прочной и жесткой, приводит к появлению сложных по форме составных конструкций, которые содержат несущие элементы в виде оболочек, пластин, а также стержней. Такую конструкцию с полным правом нельзя отнести ни к пластинам, ни к оболочкам. Поэтому для определения напряженно-деформированного состояния сложной составной конструкции необходимо разрабатывать свой собственный метод. Ниже приведена попытка разработки общего подхода к расчету конструкции, состоящей из конечного числа пластин, оболочек и стержней.
В качестве примера реализации разработанного подхода рассмотрен расчет напряженно-деформированного состояния составной конструкции, состоящей из некоторого числа идентичных блоков, скрепленных друг с другом. До настоящего времени решение такой задачи в общем виде отсутствует [1]–[10].В основе метода положен вариационно-энергетический принцип.
Рассмотрим расчет составных конструкций, состоящих из следующих элементов: пластина и оболочка [1]–[10]. Толщины, как пластинки, так и цилиндрической оболочки достаточно малы, поэтому к ним при построении теории применима гипотеза Кирхгоффа-Лява, Материал блока принят упругим, однородным, изотропным. Внешняя нагрузка считается приложенной в вершинах шестиугольных пластин оснований.
Пусть блок состоит из шестиугольной пластины (тело I) и цилиндрической оболочки (тело II). Поскольку тело I жестко скреплено с телом II, то имеет место равенство перемещений на линии соприкосновения обеих тел друг с другом.
Рассмотрим шестиугольную пластину (тело I). Пусть произвольная точка А принадлежит как телу I, так и телу II (рис. 1).
Рис. 1. – Схема для определения перемещений в точке А для тел I и II
Координаты точки А до деформации можно записать
; 
; 
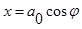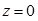. (1)
В результате деформации блока точка А перейдет в точку А1.
Координаты точки А1 после деформации равны
;
;
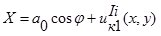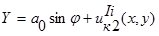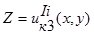. (2)
Учитывая условие (1), получим
;
;
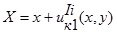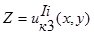. (3)
Так как точки А и А1 принадлежат телу II, их координаты можно записать в цилиндрической системе координат. До деформации точка А имела координаты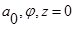 
. После деформации точка А1 будет иметь следующие координаты:
;
;
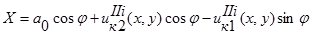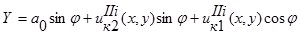. (4)
Используя (2) и (3), получим первую группу сопряжений по перемещениям:
;
;
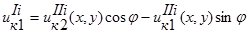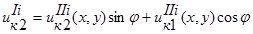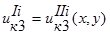. (5)
Равенство углов поворота, имеющее место при жестком скреплении тел блока, дает вторую группу условий сопряжения.
Обозначим направляющие косинусы нормали к деформированной поверхности тела I через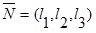 
. По формулам дифференциальной геометрии определяем координаты нормали:
;
;
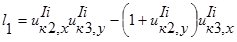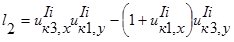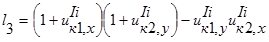. (6)
Проведем аналогичные рассуждения для тела II. Найдем деформированную образующую тела II. Для этого возьмем две произвольные, близкие друг к другу точки А и В на образующей тела II (рис. 2).
До деформации точки имеют следующие координаты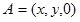 
и 
.После деформации эти точки перейдут в точки А1 и В1. С учетом (1) и (4), получим:
координаты точки А1 – 
;
; 
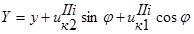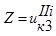. (7)
координаты точки В1 –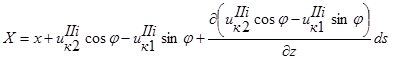 
;
;
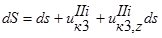. (8)
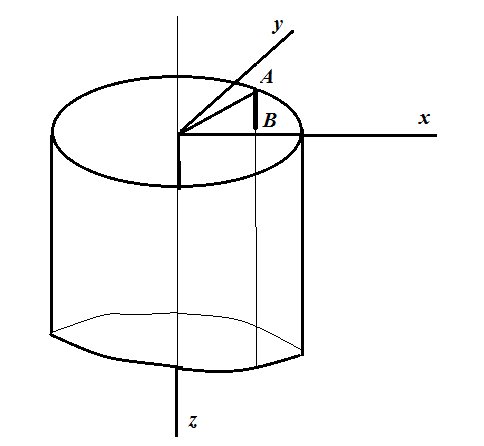
Рис. 2. – Схема для определения перемещений на образующей тела II
Тогда для тела II имеем: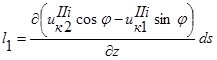 
;
; 
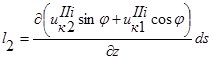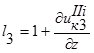. (9)
Отбрасывая малые второго порядка по сравнению с первыми, из условий (6) и (9) получим
;
;
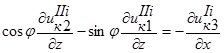. (10)
Наличие соотношений (1), (5) и (10) накладывает определенные органичения на перемещения в составной конструкции, состоящий из шестиугольной пластины (тело I) и цилиндрической оболочки (тело II).
Литература
1. Краснобаев И.А., Маяцкая И.А. Основы расчета на изгиб тонких жестких пластин [Текст]: Монография / Краснобаев И.А., Маяцкая И.А. – Ростов н/Д, РГСУ, 2011.– 87 с.
2. Краснобаев И.А., Маяцкая И.А., Смирнов И.И., Языев Б.М. Теория пластин и оболочек: [Текст]: Монография / Краснобаев И.А., Маяцкая И.А., Смирнов И.И., Языев Б.М. – Ростов н/Д, РГСУ, 2011.– 114 с.
3. Амосов А.А. Техническая теория тонких упругих оболочек: [Текст]: Монография / Амосов А.А.–М.:АСВ, 2009, – 332 с.
4. Филин А.П. Элементы теории оболочек.–Л.:Стройиздат, 1975, – 256 с.
5. Огибалов П.М., Колтунов М.Л. Оболочки и пластины.–М.:МГУ, 1969, – 696 с.
6. Calladine C.R. Theory of shell structures.– N.Y.: Cambridge University Press, 1989, –788 p.
7. Zingoni A. Shell structures in civil and mechanical engineering.– N.Y.: Thomas Telford Publishing, 1997, –351 p.
8.Литвинов В.В., Кулинич И.И. Соотношения между компонентами поверхностной нагрузки в оболочках вращения при безмоментном их состоянии.[Текст] //Интернет-журнал «Инженерный вестник Дона». 2012 №4 (2) [Электронный ресурс].-М. 2012. – Режим доступа: http://www.ivdon.ru.
9.Стрельников Г.П., Бурцева С.В., Авилкин В.И. К расчету оболочек вариационно-энергетическим методом.[Текст] //Интернет-журнал «Инженерный вестник Дона». 2012 №4 (2) [Электронный ресурс].-М. 2012. – Режим доступа: http://www.ivdon.ru.
10. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки.–М.:Наука, 1966, – 636 с.