Численное моделирование и анализ спектра системы прерывающихся сигналов
Аннотация
Дата поступления статьи: 29.03.2014В статье проведено исследование влияния прерывистости периодического сигнала на форму спектра сигнала. Проведено численное моделирование системы прерывистых гармонических сигналов и проанализирован амплитудный спектр суммарного сигнала, построенный по дискретной временной выборке. Построены графики коэффициента корреляции между спектром непрерывного сигнала и спектром системы прерывистых сигналов. Данное исследование необходимо для разработки цифровой системы определения частоты колебаний кварцевых пластин при их механической обработке.
Ключевые слова: амплитудный спектр сигнала, прерывистый сигнал, кварцевые пластины
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Задача определения основной частоты периодического сигнала часто решается путем анализа спектра записанного фрагмента сигнала. Сигнал может представлять собой сумму нескольких однотипных периодических сигналов, имеющих отклонения по частоте, амплитуде и начальной фазе. Подобная задача должна решаться, например, при измерении средней частоты колебаний группы кварцевых пластин при их механической обработке [1, 2]. За счет пьезоэлектрических свойств кварца [3, 4] при истирании пластин наблюдаются электромагнитные колебания, частота которых обратно пропорциональна толщине пластин.
В таких процессах особенностью задачи определения частоты является то, что отдельные сигналы пластин могут пропадать и вновь появляться периодично или в случайные моменты времени, то есть обладают прерывистостью [5]. В статье ставится задача исследования влияния прерывистости сигналов на форму спектра результирующего сигнала. В качестве оценки влияния возмущающих воздействий (частота прерывистости сигнала, начальная фаза прерывистости сигнала) может быть выбран коэффициент корреляции между эталонным спектром и спектром возмущенного сигнала.
Численное моделирование спектра сигнала проведено по схеме [6] и представлено на рис. 1.

Рис.1. – Этапы моделирования спектра прерывистого сигнала
Исследовано влияние прерывистости на спектр одноканального гармонического сигнала. Периодический сигнал задан функцией
![]() (1)
(1)
с параметрами A1 , f1 , ![]() 1 .
1 .
Прерывистость сигнала можно смоделировать путем умножения исходной функции (1) на функцию однополярного меандра с заданной частотой (или периодом), единичной амплитудой и скважностью.
Результирующая функция определяется:
![]() ,
,
где ![]() – функция меандра;
– функция меандра;
При моделировании выполнено условие физической реализуемости процесса возникновения колебаний, заключающееся в том, что период меандра кратен половине периода гармонического сигнала. Для задачи измерения средней частоты колебаний кварцевых пластин это означает, что колебание пластины физически может начаться только с нуля и закончиться нулем. Далее была смоделирована дискретная выборка сигнала с частотой дискретизации Fd и длиной выборки B. С помощью быстрого преобразования Фурье (БПФ) построен амплитудный спектр результирующего сигнала [6 - 10]. На рис. 1 приведены графики спектра при различных параметрах выборки и параметрах исходных функций.
Задача измерительной системы состоит в определении частоты исходной функции f1 . В приведенных примерах f1 = 100 Гц. Этой частоте соответствует центральный лепесток спектра с максимальной амплитудой. Два боковых лепестка являются "паразитными", возникающими в результате наложения на исходный сигнал функции меандра с частотой f2 . Далее с периодом в 2∙f2 пики гармоник повторяются.
Проведенное моделирование показало, что боковые лепестки меандра отстоят от центрального лепестка на величину f2 . При величине шага по частоте в амплитудном спектре более чем 0.5∙f2 боковые лепестки начинают

Рис. 2. – Спектры прерывистого гармонического сигнала при различных параметрах сигнала: f1- частота сигнала; f2 – частота прерывистости (меандра).
"сливаться" с центральным. Поэтому, чтобы обеспечить возможность поиска центральной гармоники и отсечения боковых лепестков, следует обеспечить запас по шагу. При изменении частоты f2 необходимо обратно пропорционально изменять ширину выборки:
![]()
при той же частоте дискретизации Fd. А при увеличении Fd следует пропорционально увеличить ширину выборки B для сохранения шага по частоте:
![]() .
.
Также проведено моделирование меандра с регулируемой скважностью импульсов от 0 до 1 (коэффициента заполнения). Скважность импульсов при неизменном периоде меандра пропорциональна амплитуде центральной гармоники в результирующем спектре. Боковые гармоники имеют максимум амплитуды при скважности равной ½.
Исследована зависимость коэффициента корреляции амплитудных спектров сигнала, представляющего собой сумму двух гармонических сигналов, от начальной фазы и частоты прерывистости одного из сигналов.
На рис. 3 показаны графики двух сгенерированных сигналов s1 и s2 и их суммарный сигнал Usum для параметров: f1=2000 Гц, f2=200 Гц, Fd=20 кГц, B=1024.
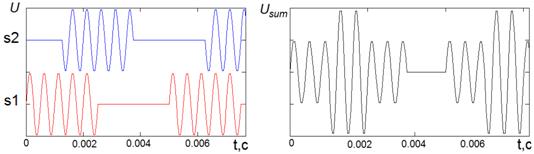
Рис. 3 – Моделирование сигнала, являющегося суммой двух прерывистых во времени гармонических сигналов: f1 – частота гармонических сигналов (равная для обеих синусоид); f2- частота прерывистости (меандра).
На рисунке сигналы сдвинуты относительно друг друга на ¼ периода меандра. Сдвиг сигналов также является регулируемым параметром при моделировании. Соответствующий сигналу амплитудный спектр A и эталонный спектр Ae представлены на рис. 4.
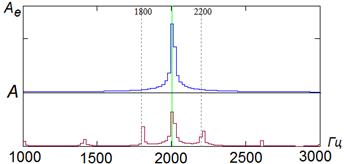
Рис. 4 – Спектры эталонного и прерывистого сигнала
Интерес представляет форма спектра в окрестности основной частоты гармонического сигнала (f1 = 2000 Гц на рис. 4). Поэтому величину коэффициента корреляции рассчитывалась для окна шириной ±10% от f1 (показано пунктиром на рис. 4). Ширина окна выбрана произвольно.
Проведено исследование влияния параметров прерывистости (частоты прерывистости и сдвига) одного из сигналов на форму результирующего спектра сигнала. Схожесть спектра эталонного (непрерывного) сигнала и спектра прерывистого сигнала оценивалась по значению коэффициента корреляции [2, 6]:
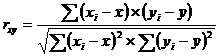 ,
,
где xi – значения вектора X(вектора амплитуд гармоник эталонного спектра); yi – значения вектора Y (вектора амплитуд гармоник спектра прерывистого сигнала); ![]() - среднее по X;
- среднее по X; ![]() - среднее по Y.
- среднее по Y.
На рис. 5 показана зависимость коэффициента корреляции от сдвига одного из сигналов (доля от периода меандра T2) при различных значениях частоты прерывистости f2.
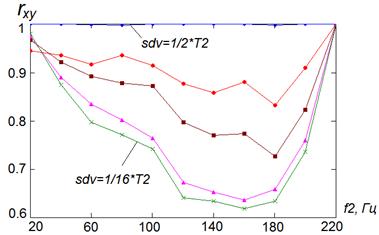
Рис. 5 – Зависимость rxy от частоты меандра f2 при различных сдвигах sdv: 1/16*T2, 1/8*T2, 1/4*T2, 1/3*T2, 1/2*T2).
Вид графиков объясняется тем, что при низкой частоте меандра его гармоники сливаются с центральной гармоникой сигнала и коэффициент корреляции достаточно высок. При увеличении частоты лепестки меандра удаляются от центрального лепестка, становятся видимыми, спектр меняет форму и коэффициент корреляции уменьшается. При увеличении частоты более 200 Гц лепестки меандра покидают исследуемое окно спектра. В результате наблюдается полное совпадение спектров и rxy =1.
Если имеется возможность измерения или расчета частоты прерывистости сигналов, то это значение частоты можно использовать для дальнейшего анализа полученного спектра и удаления из него гармоник, вызванных явлением прерывистости. Это позволит отделить "полезные" гармоники от "паразитных".
В статье исследовано влияние параметров прерывистости сигналов (частота прерывистости, начальная фаза прерывистости) на форму спектра результирующего сигнала. Результаты исследования отображены на рис. 2, 5.
Проведенные исследования могут быть полезными при разработке измерительной системы для определения основной частоты колебаний кварцевых пластин в процессе их механической обработки.
Список литературы:
1. Андросова В.Г. Справочник по кварцевым резонаторам / Андросова В.Г., Банков В.Н., Дикиджи А.Н. и др. [Текст] Под ред. П.Г. Позднякова. – М.: Связь, 1978. – 288 с.
2. Альтшуллер Г.Б., Елфимов Н.Н., Шакулин В.Г. Кварцевые генераторы: Справ. пособие. [Текст] М.: Радио и связь, 1984. – 232 с.
3. Земляков В.Л., Толмачев С.А. Диагностика пьезокерамического элемента по активной составляющей проводимости [Электронный ресурс] // Инженерный вестник Дона. 2013. №2. - Режим доступа: http://www.ivdon.ru/ magazine/archive/n2y2013/1622 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Панич А.А., Мараховский М.А., Мотин Д.В. Кристаллические и керамические пьезоэлектрики [Электронный ресурс] // Инженерный вестник Дона. 2011. №1. - Режим доступа: http://www.ivdon.ru/magazine archive/ n1y2011/325 (доступ свободный) - Загл. с экрана. – Яз. рус.
5. Guo-Xin Fan , Qing Huo Liu. Fast Fourier transform for discontinuous functions [Text] //Antennas and Propagation / IEEE Transactions on, - V. 52, Issue: , - Feb. 2004. - P. 461-465.
6. Айфичер, Э.С., Джервис, Барри У. Цифровая обработка сигналов: практический подход, 2-е издание. [Текст] Пер. с англ. – М.: Издательский дом "Вильямс", 2004. – 992 с.
7. Сергиенко, А.Б. Цифровая обработка сигналов. [Текст] СпБ.: Питер, 2003. – 604 с.
8. Оппенгейм А., Шафер Р. Цифровая обработка сигналов. [Текст] Пер. с англ. - М.: Техносфера, 2006. - 856 с.
9. Гадзиковский В.И. Теоретические основы цифровой обработки сигналов. [Текст] М: Радио и связь, 2004. – 343 с.
10. Steven W. Smith. The Scientist and Engineer’s Guide to Digital Signal Processing, Second Edition. [Text] California Technical Publishing, P.O., 1999. – 722 p.