Особенности построения модели погрешности МЭМС-датчиков при решении навигационной задачи

Аннотация

М.А. Ломакин

Дата поступления статьи: 01.06.2014

В работе описываются разработка и исследование модели погрешностей МЭМС датчиков с использованиемполиномиальной аппроксимации экспериментальных данных методом наименьших квадратовс помощью языка графического программирования LabVIEW.

Ключевые слова: Навигация, МЭМС-датчики, модель погрешностей.

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Введение
Современные датчики, базирующиеся на микроэлектромеханических системах (МЭМС), позволяют обнаруживать и измерять ускорение, отклонение, ударные нагрузки, вибрации и скорость вращения, а также осуществлять измерения с несколькими степенями свободы. Своими характеристиками, отсутствием движущихся частей, интегрированной электроникой обработки сигнала, относительно низкой ценой и малыми габаритами, миниатюрностью, функциональностью, надёжностью, малым энергопотреблением МЭМС технологии стали весьма популярны [1].
Концепция МЭМС построена на интеграции микромеханических структур датчиков (сенсорной, измерительной части) и актюаторов (исполнительной, управляющей части) с электроникой, выполняющей функции сбора, анализа, контроля, формирования управляющих сигналов на общей подложке посредством технологий микропроизводства.
В данной статье будут рассмотрены МЭМС - датчики для измерения ускорения (акселерометры) и угловой скорости (гироскопы). Данные устройства активно используются в системах управления летательными аппаратами, для обеспечения безопасности движения автомобилей, в сельскохозяйственной технике, изделиях специального назначения, в инерциальных системах навигации и др. В настоящее время существует достаточно много различных устройств с интегрированными МЭМС датчиками, но существует ряд проблем и недостатков, связанных с работой данных датчиков [2].
Одним из значимых недостатков микроэлектромеханических (МЭМС) инерциальных датчиков является сравнительно низкая точность и зашумленность выходного сигнала дрейф смещения нуля [3], учитывая характер математических преобразований при решении навигационной задачи (интегрирование), дрейф нуля существенно влияет на качество ее решения [4, 5]. Ниже приведено описание эксперимента, целью которого была разработка математической модели данного вида погрешности МЭМС датчиков (акселерометр и датчик угловых скоростей).
Математическое обоснование
Для построения кривой, которая воспроизводила бы график исходной экспериментальной закономерности (дрейф нуля), т.е. была бы максимально близка к экспериментальным точкам, но в то же время была нечувствительна к случайным отклонениям измеряемой величины, необходимо получить модели погрешности набора экспериментальных данных МЭМС датчиков.
Нахождение погрешности осуществляется при помощи разности между кривой аппроксимирующей функцией и исходным набором данных. Наиболее распространенным методом аппроксимации экспериментальных данных является метод наименьших квадратов (МНК) [6]. Метод позволяет использовать аппроксимирующие функции произвольного вида. Для табличных данных, полученных в результате эксперимента, где i=0,1,…,n, построим аппроксимирующий многочлен

(1)

причем, для которого:

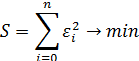(2)

При использовании аппроксимации МНК стоит обратить внимание, что при больших степенях полинома для входных значений может возникнуть «потеря значности» (обращение коэффициентов при высших степенях в ноль). Это чревато ростом погрешности. С одной стороны слишком большая степень полинома ведет к повышенной его осцилляции [7] (явление полиномиального раскачивания). Поэтому к степеням выше 5 - 6 обычно не прибегают. Однако, с другой стороны, слишком малая степень полинома ведет к росту погрешности аппроксимации и, как следствие, увеличению среднеквадратичного значения (СКЗ) погрешности МЭМС датчиков [8].
Для проведения исследований модели погрешностей МЭМС датчиков было использовано программное обеспечение, разработанное при помощи графического языка программирования «G» фирмы National Instruments (США) LabVIEW. Работая над созданием стенда, с помощью которого можно исследовать процессы поведения модели погрешностей МЭМС датчиков, была разработана структурная схема, в соответствии с рисунком 1.

На структурной схеме видно, что полученные данные, поступающие с цифрового выхода МЭМС - датчиков, непосредственно связанного с микроконтроллером, не подвергаются аналоговой фильтрации. Для передачи данных из микроконтроллера в ПК был создан протокол передачи данных. Обмен информации осуществляется путем формирования пакетов данных по каждой из оси трехосевого акселерометра и датчика угловых скоростей. Далее, при помощи преобразователя интерфейсов, данные отправляются по USB 2.0 в ПК, где подвергаются обработке [9, 10].
Описание эксперимента
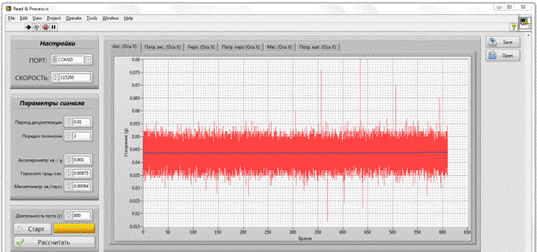
Для наглядности эксперимента была разработана тестовая программа в среде разработки LabVIEW, в которой отображалась зависимость изменения показаний МЭМС датчиков от времени. Графики и внешний вид программы представлены на рисунке 2.

Рисунок 2 - Тестовая программа

Для сравнительного анализа модели погрешности датчиков требуется построение кривых разности между аппроксимирующими функциями различной степени полинома и исходным набором данных. Кривая погрешности МЭМС акселерометра представлена на рисунке 3.

Рисунок 3 - Кривая разности аппроксимации полиномом второй степени и исходным набором данных

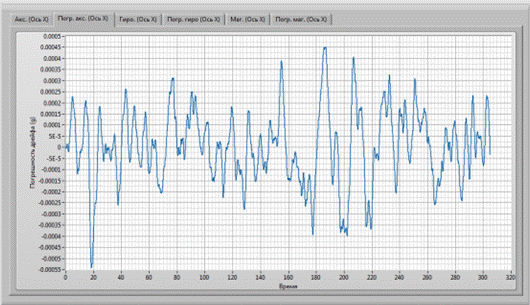
На рисунке 4 изображена кривая разности аппроксимации полиномом третей степени и исходным набором данных погрешности МЭМС акселерометра.

Рисунок 4 - Погрешность МЭМС акселерометра

На рисунке 5 изображена кривая разности аппроксимации полиномом четвертой степени и исходным набором данных погрешности МЭМС акселерометра.

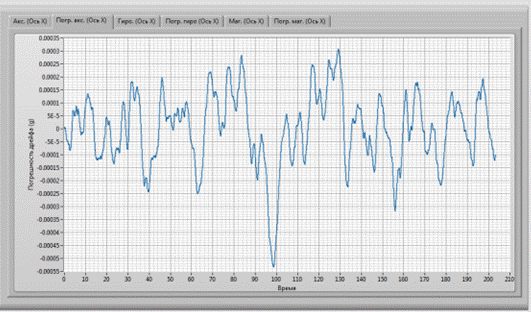
На рисунке 6 изображена кривая разности аппроксимации полиномом четвертой степени и исходным набором данных погрешности МЭМС акселерометра.

Рисунок 6 - Погрешность МЭМС акселерометра

В таблице 1 представлено среднеквадратичное значение (СКЗ) погрешностей МЭМС датчиков рассчитанных по кривой разности между кривой аппроксимирующего многочлена, вычисленного при помощи метода наименьших квадратов с различными полиномиальными степенями и исходным набором данных.

Выводы
Проанализировав полученные коэффициенты СКЗ погрешности МЭМС датчиков, полученных при помощи разности между кривой аппроксимирующего многочлена, вычисленного при помощи метода наименьших квадратов с различными полиномиальными степенями и исходным набором данных, было выявлено, что дальнейшее увеличение степени полинома нецелесообразно и достаточно ограничиться аппроксимацией экспериментальных данных МЭМС датчиков полиномом четвертой степени методом наименьших квадратов.
Результаты исследований, изложенные в данной статье, получены при финансовой поддержке Минобрнауки РФ в рамках реализации проекта «Создание высокотехнологичного производства для изготовления комплексных реконфигурируемых систем высокоточного позиционирования объектов на основе спутниковых систем навигации, локальных сетей лазерных и СВЧ маяков и МЭМС технологии» по постановлению правительства №218 от 09.04.2010 г. Исследования проводились в ФГАОУ ВПО ЮФУ.

Литература:

1. Крекотень Ф.В. Современные МЭМС-гироскопы и акселерометры [Текст] / Ф.В. Крекотень // «Петербургский журнал электроники». - №1. - 2011 г. – С. 81 – 96.
2. Б.Г. Коноплев, И.Е. Лысенко, Е.В. Шерова. Интегральный сенсор угловых скоростей и линейных ускорений [Электронный ресурс] / «Инженерный вестник Дона», 2010, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2010/240 (доступ свободный) – Загл. с экрана. – Яз. рус.
3. И.В. Щербань, С.А. Толмачев, С.О. Красников. Универсальная стохастическая модель произвольного движения наземного транспортного средства [Электронный ресурс] / «Инженерный вестник Дона», 2013, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1812 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Weston, J. L. Basic Principles Of Strapdown Inertial Navigation Systems [Text] / J. L. Weston // Strapdown Inertial Navigation Technology – 2nd Edition. – Radar, sonar, navigation and avionics, 2004. – Chapter 3. – P. 17 - 59.
5. Sukkarieh, S. Low Cost, High Integrity Aided Inertial Navigation Systems For Autonomous Land Vehicles [Text]: Ph.D. Thesis, Univ. of Sydney, 2000. – 136 p.
6. Линник Ю. В.  Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений [Текст] / Ю. В. Линник. — 2-е изд. — М.: Физматгиз, 1962. – 349 с.
7.  Поршнев С.В. Компьютерный анализ и интерпретация эмпирических зависимостей [Текст] / А. В. Каплан, В. Е. Каплан, М. В. Мащенко, Е. В. Овечкина // под ред. С.В. Поршнева. - Изд-во: Бином-Пресс, 2009 г., 336 с.
8. Среднеквадратическая погрешность [Электронный ресурс] //Большая Энциклопедия Нефти Газа - Режим доступа: http://www.ngpedia.ru/id271295p1.html (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Пешехонов, В.Г. Интегрированные инерциально-спутниковые системы навигации: сб. ст. и докл. [Текст] – СПб.: Электроприбор, 2001. – 235с.
10.  Sukkarieh, S. Low Cost, High Integrity Aided Inertial Navigation Systems For Autonomous Land Vehicles [Text]: Ph.D. Thesis, Univ. of Sydney, 2000. – 136 p.