Оптимальное интерполирование типовых динамик в задаче управления с прогнозированием

Аннотация

Н. И. Гданский, А.В. Карпов, А.А. Бугаенко

  В статье рассмотрены оптимальные способы сплайнового интерполирования траекторий углового перемещения по узловым точкам при решении задач управления движением с прогнозированием внешней нагрузки. В качестве критериев оптимальности рассмотрены точность аппроксимации работы привода и трудоемкость  расчета коэффициентов сплайнов.

Ключевые слова: Траектория перемещения, сплайны Лагранжа, сплайны Фергюссона, интерполяция

05.13.06 - Автоматизация и управление технологическими процессами и производствами (по отраслям)

Основным путем повышения эффективности оборудования является автоматизация основных и вспомогательных производственных операций. Выполнение последних, как правило, сопровождается недетерминированным изменением внешней нагрузки на приводах. В работе [1] предложено в таких случаях для управления перемещением по заданному закону в системе с одной степенью свободы φ использовать прогнозирование недетерминированной внешней нагрузки, представленной в виде сложной функции M(t,φ(t)) по времени t. Ее математическую модель представлена в виде  скалярного произведенияM (t,φ(t)) = (^¯M ^k,^¯φ^k(t)), в котором ^¯M ^k - состоящий из частных производных по t и φ  силовой вектор порядка k (максимальный порядок производных), ^¯φ^k(t) - соответствующий ему кинематический вектор.
В качестве промежуточной величины для расчета управляющего воздействия предложено использовать работу А, которую должен совершать привод на заданном временном отрезке управления [t_i, t_i+₁]. Для принятой модели внешней нагрузки формула для А как функции времени t принимает общий вид:
.  (1)      
Практически малые угловые перемещения регистрируют при помощи инкрементных датчиков, выдающих дискретные импульсы при угловом смещении вала на фиксированный шаг, величину которого обозначим через h. Поэтому для сокращения формульных выражений при данном способе измерения угловых перемещений наряду с обычной работой рассмотрим приведенную работу, равную обычной, деленной на шаг h:    Безразмерные инкрементные угловые перемещения вала обозначим через y, а время (t -t₀) относительно начала измерений - через t.
Для модели нагрузки первого порядка (k =1) выражение для приведенной работы  через вектор ^¯M ^k имеет вид:
    (2)
При  k =2  выражение  (^¯M ²,^¯ Ψ²(τ))  имеет вид:
         
   (3)
Исходную информацию для расчета управляющего воздействия задают следующие данные обратной связи: 1) массив моментов времени {t_i} с зарегистрированными сигналами инкрементного датчика; 2) массив значений работ {А_i} на отрезках [t_i,t_i+1]. Для получения из формул (^¯M^k,^¯Ψ^k(τ)) линейных уравнений относительно коэффициентов силового вектора^¯M ^k на каждом отрезке управления [t_i, t_i+1] в эти зависимости должно быть подставлено уравнение некоторой кривой Ψ_i(τ), задающей перемещение управляемого звена внутри данного отрезка.
В работе [1] использована простейшая кусочная интерполяция траектории перемещения объекта управления при помощи сплайнов Лагранжа - отрезков прямых, проходящих через узловые точки. Однако численные расчеты показывают, что точность расчета интегралов в выражениях (2) и (3) при этом невысока и для получения лучшего приближения зависимости (^¯M^k,^¯Ψ^k(τ)) необходимо использовать другие виды степенных сплайнов Ψ_i(t) более высокого порядка по  t. Помимо численной близости к точным значениям интегралов в (2) и (3), второй существенной качественной характеристикой сплайнового приближения является трудоемкость алгоритмов расчета коэффициентов сплайнов. Она особенно актуальна при использовании в качестве вычислительных устройств в системах управления микроконтроллеров.
Интегралы в (2) и (3) представим их в обобщенном виде
   (4)
в котором степени p,q и r -неотрицательные целые числа.
При данном обозначении формулы (2) и (3) принимают вид:
1. k =1:
     (5)
2. k =2:
  (6)
Таким образом, качество интерполирования величин работ (2) и (3) определяется точностью, с которой сплайны приближают следующие 6 интегралов, которые назовем траекторными:
I_110(i), I_120(i), I_211(i), I_210(i), I_220(i), I_230(i).  (7)
Поскольку линейные сплайны дают невысокую точность приближения,  для вычисления траекторных интегралов (7) рассмотрим возможности квадратичных и кубических локальных сплайнов, имеющих порядок 2 и 3, а также кубических интерполяционных сплайнов Фергюссона.
Отрезок [τ_i,τ_i+1], на котором строится интерполирующий сплайн, для краткости назовем интерполируемым.  Наряду с ним рассмотрим также соседние с ним отрезки [τ_i-1,τ_i] и [τ_i+1,τ_i+2], которые назовем окрестностью интерполируемого отрезка.
Общее уравнение сплайна второго порядка для отрезка [τ_i, τ_i+1] для более удобного выполнения преобразований представим в виде: Ψ_i(t) = C_0(i) + C_1(i) τ+ C_2(i) τ²/2, где C_0(i), C_1(i), C_2(i)  - константы. К данному типу сплайнов отнесём:
- сплайн по усредненным первым производным в крайних точках отрезка интерполирования: C_2(i) = (Ψ_i’(τ_i+1)- Ψ_i’(τ_i)) / l_i; C_1(i)  = Ψ_i’(τ_i) - C_2(i)τ_i; Ψ_i’ =(ΔΨ_i-1+ΔΨ_i)/(l_i-1+ l_i); Ψi’_i+1 =(ΔΨ_i+ΔΨ_i+1)/(l_i+ l_i+1)),
- сплайн по взвешенным первым производным в крайних точках отрезка интерполирования: Ψ’_iв =(ΔΨ_i-1+2Δ_Ψi)/(l_i-1+ 2l_i); Ψ’_(i+1)=(2ΔΨ_i+ΔΨ_i+1)/(2l_i+ l_i+1)).
Общее уравнение сплайна порядка 3 для отрезка [τ_i, τ_i+1] представим в виде:
Ψ_i(t) = C_0(i) + C_1(i) τ+ C_2(i) τ²/2 + C_3(i) τ³/3,     где C_0(i), C_1(i), C_2(i), C_3(i)   - константы.
К таким сплайнам относятся:
- сплайны Фергюссона[2],
-  сплайн по усредненным первым производным в крайних и средней точке отрезка интерполирования: C_3(i)=(2Ψ’_срi - Ψ’i+1 - Ψ’_i)/(2_τсрi² _- τ_i+1²- τ_i²) = 2(Ψ’_i+1 + Ψ’i - 2Ψ’ср_i)/l²_i; C_2(i)= 2[Ψ’_срi -  Ψ’_i  - C_3(i) (τ _срi ² - τ_i² )]/l_i; C_1(i) =Ψ’_i  - C_2(i)τ_i - C_3(i)τ_i²; Ψ’_i  =(ΔΨ_i-1+ΔΨ_i)/(l_i-1+ l_i); Ψ’_i+1 =(ΔΨ_i+ΔΨ_i+1)/(l_i+ l_i+1); Ψ’_срi= ΔΨ_i / l_i),
- сплайн по взвешенным первым производным в крайних точках отрезка интерполирования: Ψ’i   =(ΔΨ_i-1+2ΔΨ_i)/(l_i-1+ 2l_i); Ψ’_i+1 =(2ΔΨ_i+DΨ_i+1)/(2l_i+ l_i+1); Ψ’_срi = ΔΨ_i / l_i..
Введем следующие обозначения:
-^¯m^k-вектор частных производных, входящих в силовой вектор¯M^k порядка k,
- р – длина вектора^¯m^k,
-^¯I _(i) ,^¯I_пр(i) - векторы точных интегралов при коэффициентах вектора¯m^k для отрезка [τ _i,τ _i+1] и приближенных интегралов, соответствующих выбранному методу интерполирования траектории.
Точное значение приведенной работы на отрезке [τ _i,τ _i+1] равно:
   (8)
Приближенное значение приведенной работы на отрезке [τ _i,τ _i+1] при выбранном методе интерполирования на заданной траектории выражается:
  (9)
Разность точного и приближенного значений работы на отрезке [τ _i,τ _i+1]:

Используя неравенство Коши — Буняковского, оценим абсолютную величину разности работ, используя норму векторов в евклидовом пространстве:
      (10)
где
Оценим разность работ для совокупности n подряд идущих отрезков времени [τ₀=0,τ₁], [τ₁,τ₂],...,[τ_n-1,τ_n]. Так как при построении сплайнов наряду с интерполируемым отрезком необходимо использовать данные о функции на его окрестности, то суммирование применим по всем отрезкам кроме крайних с номерами 0 и (n -1):
    (11)
Полученная оценка точности расчета приведенной работы для всей траектории зависит от метода интерполирования (обозначим его Mth),  формы траектории (которую обозначим Tr) и модуля вектора точных значений интегралов I _(i), от вектора частных производных¯m^k и порядка модели k: Выделим в полученной формуле величину, зависящую преимущественно от метода ее интерполирования, формы траектории и порядка модели k:
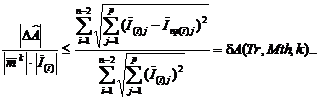    (12)
. Назовем величину относительной погрешностью расчета полной работы, а δA(Tr,Mth,k) - гарантированной точностью ее расчета. Примем последнюю в качестве оценочного критерия влияния метода интерполирования на относительную погрешность расчета работы  при выбранном методе интерполирования Mth на траектории Tr. Гарантированное качество выполнения интерполирования траектории заданным методом интерполирования возрастает с уменьшением величины δA(Tr,Mth,k).
Практически в методах управления с прогнозированием внешней нагрузки необходимо использовать модели нагрузки порядков от 0 до максимального значения k.=2 Поскольку в начало вектора коэффициентов¯Mk модели нагрузки максимального порядка k входят все коэффициенты векторов¯M1 всех моделей нагрузки более низких порядков q<k, то при минимальной величине δA(Tr,Mth,k), будут близки к минимальным значения δA(Tr,Mth,q). Поэтому для оценки качества интерполирования достаточно определить оптимальный метод интерполирования для максимального порядка k = 2.
В качестве тестовых рассмотрено 9 кривых. На каждой из них выбрано 16 точек (Ψ_i=i,τ_i),(i=0,...,n=15), которые моделируют инкрементный способ измерения перемещения с шагом 1 на 15, при котором выполняется условие: Ψ_i+1 - Ψ_i = 1,(i = 0, ... , n-1=14). Тестовыми являются следующие типовые виды перемещений:

1. Линейное перемещение: Ψ₁(τ)=τ¹; τ(1)_i=i.
2. Квадратичное перемещение: Ψ₂(τ)=τ²; τ(2)_i=.
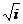3. Кубическое перемещение:  Ψ₃(τ) =t3;  τ(3)_i= .
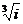4. Парабола 4 степени:  Ψ₄ (τ)=τ4;  τ(4)_i=.
5. Перемещение по графику квадратного корня: Ψ₅(τ) = ; i= i²-1.
6. Перемещение по графику кубического корня:  Ψ₆(τ) = 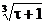;  τ₍₆₎i= i³-1.
7. Перемещение по графику корня 4 степени:  Ψ₇ (τ) = 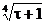; τ₍₇₎i =  i⁴-1.
8. Перемещение по кубической параболе с точкой перегиба:  Ψ₈ (τ) = τ²(8-τ/3)/45 .
9. Перемещение по синусоиде:  Ψ₉ (τ) = 16×sin(τ);  τ₍₉₎i= arcsin(i/16).


10. Вектор интегралов (точных и приближенных)^¯I при коэффициентах вектора^¯m^k следующим образом выражается через траекторные интегралы:
    ¯I = (I₁₁₀, I₁₂₀+I₂₁₁, I₂₁₀, I₂₂₀, I₂₃₀). (13)
    Формула для гарантированной точности δA(Tr,Mth,2) расчета относительной приведенной работы в модели нагрузки второго порядка траектории Tr_s с номером s с использованием метода ее интерполированияMth_r с номером r принимает вид:
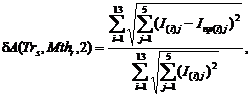    (14)
    где для выбранной траектории Tr_s:
    I_(i)j – точное значение интеграла при коэффициенте вектора^¯m² с номером j для участка Tr_s с номеромi,
    I _пр(i)j – аналогичное приближенное значение интеграла при коэффициенте вектора^¯m² с номером j для участка Tr_s с номером i, соответствующее методу интерполирования Mth_r.Результаты расчетов приведены в таблице 1.

Табл.1. Точность относительной погрешностью расчета полной работы

Сравнение качества приближения по отдельным кривым показывает, что:
1) кубические интерполяционные сплайны Фергюссона (№3) дают  лучший результат  для 6 кривых из 8 рассмотренных,
2) кубические локальные сплайны по усредненным производным в крайних и средней точке  (№4)  дают  лучший результат для 2 кривых из 8.
Анализ суммарной погрешности δ_Σ показывает, что наилучшие результаты дает использование кубических сплайнов:
1) интерполяционные сплайны Фергюссона (№3),  δ_Σ  = 0,02744,
2) локальные сплайны по усредненным производным в крайних и средней точке (№4),  δ_Σ  = 0,0315237,
3) локальные сплайны по взвешенным производным в крайних точках отрезка (№5),  δ_Σ  = 0,07014868.
Рассмотрим трудоемкость вычисления коэффициентов данных сплайнов. Поскольку вычисление коэффициентов у кубических локальных сплайнов по взвешенным производным в крайних точках отрезка (№5) более трудоемко, чем у аналогичных сплайнов (№4), а точность хуже, то  данные сплайны из анализа исключаем.
Отличительной особенностью используемых сплайнов является то, что их коэффициенты должны определяться для глобальной переменной.
Расчет n сплайнов Фергюссона для локальных переменных требует выполнения:  9n-3 сложения, 8n-3 умножений, 4n-2 деления. Однако при переходе к каноническому виду по глобальной переменной суммарные вычислительные затраты резко вырастают до: 28n-3 сложения, 36n-3 умножений, 6n-2 деления. Прямой расчет данных коэффициентов без использования полиномов Эрмита позволяет снизить вычислительные затраты до: 16n-18 сложений, 12n-5 умножений, 4n-2 деления.
Рассмотрим расчет n кубических локальных сплайнов по усредненным производным в крайних и средней точке (№4). Поскольку в расчетных формулах для их коэффициентов повторяется ряд величин, их целесообразно рассчитать до начала основного расчета:
1) τ_(i)кв=τi²,  (i = 0,1,...,n+1);  2) ΔΨ_i = Ψ_i - Ψ_i-1, (i = 0,1,...,n+1); 
3)  l _i = τ_i - τ_i-1, (i = 0,1,...,n+1);  4)  Ψ_i’  =(ΔΨ_i-1+ΔΨ_i)/(l_i-1+ l_i) (i = 1,...,n+1) .
Расчетные формулы для каждого сплайна с номером i (i - ,1,...,n):
Ψ’_срi = ΔΨ_i / l_i ;  τ _срi = 0,5(τ_i + τ_i-1);    C_3(i) = 2(Ψ’_i+1 + Ψ’_i - 2Ψ’_срi)/l²_i;
 C_2(i)= 2[Ψ’_срi -  Ψ_i’ - C_3(i) (τ _срi ² - τ_(i)кв)]/l_i;      C_1(i) =Ψ_i’ - C_2(i)τ_i - C₃(i^τ_(i)кв .
Суммарные вычислительные затраты составляют: 10n+4 сложения, 12n+3 умножения, 4n +1 деление.  Существенное снижение по сравнению с прямым расчетом коэффициентов сплайнов Фергюссона  получено только по сложению (6n). Число остальных операции с точностью до постоянных слагаемых одинаково. Поэтому оптимальным вариантом в задачах управления с прогнозированием является применение интерполяционных  сплайнов Фергюссона с использованием прямого расчета их коэффициентов по глобальной переменной.

Список литературы: 

  1.Марченко Ю.А. Адаптивный цифровой алгоритм программного управления в условиях переменной внешней нагрузки. // Химическое и нефтегазовое машиностроение. №12, 2010. – с. 34-36.
2. Гданский Н.И. Геометрическое моделирование и машинная графика. – М.: МГУИЭ, 2003 г. – 236 с.