Исследования направлений повышения эффективности автомобильного транспорта леса
Аннотация
В статье предлагается модель оптимизации грузоперевозок продукции лесопромышленного предприятия, которая описывает процесс перевозки леса от лесозаготовительных предприятий к лесоперерабатывающим предприятиям. В модели рассматривается поиск оптимального кратного контура транспортной сети.
Ключевые слова: математическая модель, оптимизация грузоперевозок, автомобильный транспорт леса, многопродуктовая транспортная задача
05.13.18 - Математическое моделирование, численные методы и комплексы программ
В условиях реформирования российской экономики эффективность использования лесных ресурсов оценивается исследователями как неудовлетворительная и существенно уступает зарубежной, а проводимые в лесном секторе преобразования далеки от прогрессивных и ориентированных на упрочение лесных богатств страны – они, зачастую, конъюнктурны, не системны и неудачно компилируют отдельные элементы зарубежной лесной политики [1], [2]. Для восстановления позиций российского лесопромышленного комплекса в мировой экономике и ухода от «сырьевой» ориентации экспорта требуются новые технологические и организационно-экономические исследования, важнейшую роль среди которых играют исследования в области автомобильного транспорта леса [3].
Вывозка леса лесовозными автопоездами – важнейшая часть производственного процесса лесозаготовок, во многом определяющая стоимость лесоматериалов и эффективность работы лесозаготовительных предприятии и варианты их связей с потребителями древесины. Затраты на транспорт составляют до 48 % от себестоимости ее заготовки. Доля автотранспорта в общем объеме вывозки древесины примерно 85 % и продолжает повышаться. Наряду с сохранением в нашей стране вывозки леса в хлыстах на нижние склады лесозаготовительных предприятии в настоящее время существенно возрастает объем транспортировки в сортиментах непосредственно с лесосек потребителям и на перерабатывающие предприятия [4], [5], [6].
Эффективность использования транспортных средств на вывозке леса может быть обеспечена только при рационально организованном процессе оперативного управления транспортом с использованием современных экономико-математических методов и информационных систем.
Математическое моделирование процессов управления в данный момент является одним из основных инструментов определения оптимальных параметров функционирования различных производственных систем. Модели, построенные на основании некоторых свойств исследуемого объекта, позволяют сделать вывод о дальнейшем развитии объекта и его составных подсистем, а также изменения его основных количественных характеристик. Методы и средства математического моделирования в сочетании с использованием современных компьютерных технологий позволяют весьма эффективно решать задачи эффективной организации материальных потоков и управления их деятельностью [7], [8].
Таким образом, применяя методы управления производством, учитывающие природно-климатические и почвенно-грунтовые условия, в которых работает предприятие, а также стратегию обновления, пополнения и ремонта парка машин, можно существенно повысить эффективность лесозаготовительного процесса, снизить затраты на выработку лесопродукции и увеличить рентабельность предприятия.
Целью диссертационной работы является снижение транспортных издержек на перевозку лесоматериалов между лесозаготовительными и лесоперерабатывающими предприятиями лесопромышленного региона на базе математического моделирования.
Разработана математическая модель управления производственными мощностями лесотранспортного предприятия, позволяющую предприятию получить максимальный доход от распределения инвестиций в заданный период времени.
Зависимость дохода предприятия в период ![]() от его мощности зададим уравнением вида:
от его мощности зададим уравнением вида: ![]() (1)
(1)
где ![]() - прибыль предприятия за период
- прибыль предприятия за период ![]() ;
; ![]() - мощность парка машин в период времени
- мощность парка машин в период времени ![]() ;
; ![]() - коэффициенты зависимости дохода предприятия от мощности парка, учитывающие сезонный характер работ.
- коэффициенты зависимости дохода предприятия от мощности парка, учитывающие сезонный характер работ.
Учитывая амортизацию и инвестиции в период времени ![]() , найдём выражение для мощности парка машин в период времени
, найдём выражение для мощности парка машин в период времени ![]() :
:![]() (2)
(2)
где ![]() - мощность парка машин в период времени
- мощность парка машин в период времени ![]() ;
; ![]() - инвестиции в начале периода
- инвестиции в начале периода ![]() ;
; ![]() - коэффициент амортизации парка лесовозных автомобилей.
- коэффициент амортизации парка лесовозных автомобилей.
Сформулируем задачу оптимального распределения инвестиций в заданный период времени, позволяющую предприятию получить максимальный доход:
 (3)
(3)
где ![]() - суммарные инвестиции за весь период
- суммарные инвестиции за весь период ![]() .
.
Используя метод множителей Лагранжа, получаем оптимальное распределение инвестиций в различные периоды времени:
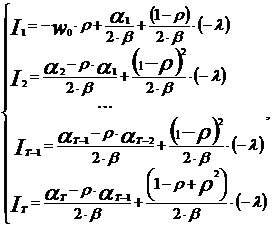 (4)
(4)
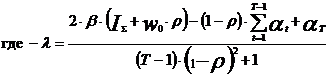
Данная математическая модель учитывает сезонный характер работ, амортизацию парка лесовозных автомобилей, коэффициент которой изменяется с течением времени, а также разбиение парка машин на разные классы по маркам и возрастам.
Предложена математическая модель оптимизации парка машин лесозаготовительного предприятия, интегрированного в лесоперерабатывающий холдинг, позволяющая оптимизировать транспортные затраты путём минимизации порожнего пробега, учитывающая затраты на заготовку древесины в точках рубки при заданной максимальной границе, штраф за недорубленную древесину, продажу другим потребителям, а также внешнюю закупку у других потребителей.
Таким образом, модель предполагает составление оптимального плана рубки для удовлетворения спроса потребителей с учётом транспортных затрат и ряда ограничений, сформулированных выше.
Для отражения экономических взаимоотношений между лесозаготовительными предприятиями и лесоперерабатывающими предприятиями строится матрица производственно-транспортных затрат, которая выглядит следующим образом:
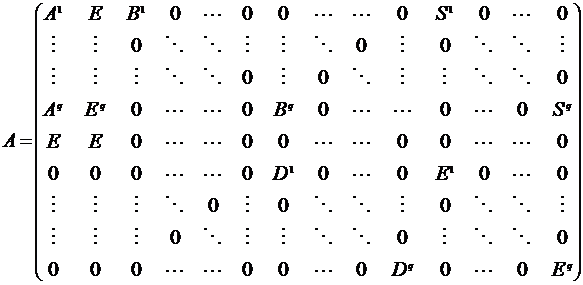 (5)
(5)
где  - матрица, показывающая затраты на заготовку единицы продукции,
- матрица, показывающая затраты на заготовку единицы продукции, ![]() - матрица максимально допустимых объёмов продаж лесосырья,
- матрица максимально допустимых объёмов продаж лесосырья, ![]() - матрица минимальных объёмов закупки лесосырья,
- матрица минимальных объёмов закупки лесосырья, 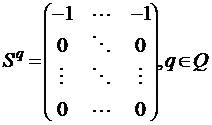 - матрица транспортных затрат для пунктов производства.
- матрица транспортных затрат для пунктов производства.
Далее осуществляется переход от матрицы транспортно-производственных затрат к маршрутной матрице, столбцы которой являются множествами заранее сгенерированных ординарных, четных и нечетных маршрутов: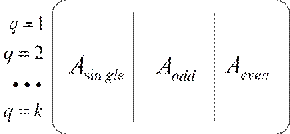 (6)
(6)
где ![]() - множество ординарных маршрутов (маршрутов, соединяющих один пункт производства и один пункт потребления);
- множество ординарных маршрутов (маршрутов, соединяющих один пункт производства и один пункт потребления); ![]() - множество нечётных маршрутов (маршрутов, соединяющих два пункта производства с двумя пунктами потребления, при этом осуществляя нечётное количество перевозок);
- множество нечётных маршрутов (маршрутов, соединяющих два пункта производства с двумя пунктами потребления, при этом осуществляя нечётное количество перевозок); ![]() - множество чётных маршрутов (маршрутов, соединяющих два пункта производства с двумя пунктами потребления, при этом осуществляя чётное количество перевозок).
- множество чётных маршрутов (маршрутов, соединяющих два пункта производства с двумя пунктами потребления, при этом осуществляя чётное количество перевозок).
Для каждого типа маршрута опишем правила построения столбца маршрутной матрицы ![]() . Ординарный маршрут
. Ординарный маршрут ![]() характеризуется следующей спецификацией:
характеризуется следующей спецификацией:
 (7)
(7)
где ![]() — количество повторений циклов типа:
— количество повторений циклов типа:
![]()
Для чётного маршрута ![]() используем следующую спецификацию столбца маршрутной матрицы:
используем следующую спецификацию столбца маршрутной матрицы:
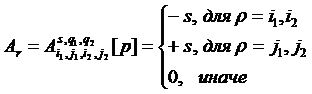 (8)
(8)
где ![]() — количество повторений циклов типа
— количество повторений циклов типа

Для нечётного маршрута столбцы матрицы выглядят следующим образом: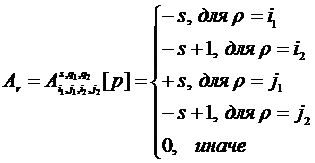 (9)
(9)
где ![]() — количество повторений циклов типа
— количество повторений циклов типа
 .
.
Исходя из предложенной классификации маршрутов, вычисляем ряд их параметров, таких как длина, время передвижения лесовозного автомобиля и затраты на реализацию данного типа маршрута. Покажем параметры для нечетного маршрута (остальные параметры для других типов маршрутов вычисляются аналогичным образом)
Длина нечётного маршрута ![]() определяется следующим образом:
определяется следующим образом:
![]() (10)
(10)
где ![]() — длина дуги, соединяющей гараж с пунктом производства
— длина дуги, соединяющей гараж с пунктом производства ![]() ;
; ![]() — длина дуги, которая связывает пункт потребления
— длина дуги, которая связывает пункт потребления ![]() и гараж;
и гараж;
![]() — длина дуги, по которой осуществляется перевозка продукции вида
— длина дуги, по которой осуществляется перевозка продукции вида ![]() от производителя
от производителя ![]() к потребителю
к потребителю![]() ;
; ![]() — длина дуги, по которой осуществляется перевозка продукции вида
— длина дуги, по которой осуществляется перевозка продукции вида ![]() от производителя
от производителя ![]() к потребителю
к потребителю ![]() ;
; ![]() — длины дуг, по которым осуществляется порожний пробег лесовозного автомобиля;
— длины дуг, по которым осуществляется порожний пробег лесовозного автомобиля; ![]() — количество перевозок.
— количество перевозок.
Время передвижения лесовозного автомобиля по нечетному маршруту ![]() вычисляется по формуле:
вычисляется по формуле: (11)
(11)
где ![]() — время передвижения по дуге, которая соединяет гараж с пунктом производства
— время передвижения по дуге, которая соединяет гараж с пунктом производства ![]() ,
, ![]() — время передвижения автомобиля из пункта потребления
— время передвижения автомобиля из пункта потребления ![]() в гараж;
в гараж; ![]() — время передвижения по дуге, связывающей производителя
— время передвижения по дуге, связывающей производителя ![]() продукции вида
продукции вида ![]() с потребителем
с потребителем ![]() ;
; ![]() — время передвижения лесовозного автомобиля из пункта производства
— время передвижения лесовозного автомобиля из пункта производства ![]() продукции вида продукции вида
продукции вида продукции вида ![]() с потребителем
с потребителем ![]() ;
; ![]() — время, затраченное на порожний пробег лесовозного автомобиля;
— время, затраченное на порожний пробег лесовозного автомобиля; ![]() — количество перевозок.
— количество перевозок.
Затраты на реализацию нечётного маршрута ![]() представляются следующим образом:
представляются следующим образом:
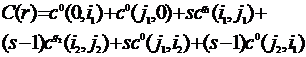 (12)
(12)
где ![]() — затраты на передвижение по дуге, соединяющей гараж с пунктом производства
— затраты на передвижение по дуге, соединяющей гараж с пунктом производства ![]() ,
, ![]() — затраты на передвижение автомобиля из пункта потребления
— затраты на передвижение автомобиля из пункта потребления ![]() в гараж;
в гараж; ![]() — затраты на передвижение по дуге, связывающей производителя продукции вида
— затраты на передвижение по дуге, связывающей производителя продукции вида ![]() с потребителем
с потребителем![]() ;
; ![]() — затраты на передвижение лесовозного автомобиля из пункта производства
— затраты на передвижение лесовозного автомобиля из пункта производства ![]() продукции вида продукции вида
продукции вида продукции вида ![]() в пункт потребления
в пункт потребления![]() ;
;
![]() — затраты на порожний пробег лесовозного автомобиля;
— затраты на порожний пробег лесовозного автомобиля; ![]() — количество перевозок.
— количество перевозок.
Анализируя параметры маршрута можно сделать выводы о допустимости маршрута. Далее введём критерии допустимости маршрута, которые необходимы для определения оптимальности текущего решения. Зададим множество критериев допустимости маршрутов:![]() (13)
(13)
где ![]() — критерий времени движения по маршруту
— критерий времени движения по маршруту ![]() ;
; ![]() — критерий длины маршрута
— критерий длины маршрута ![]() ;
; ![]() — критерий затрат на реализацию маршрута
— критерий затрат на реализацию маршрута ![]() .
.
Критерии допустимости маршрута соответствуют определённым ранее параметрам маршрута. Для каждого типа маршрутов определим множество допустимых маршрутов. Множество допустимых ординарных маршрутов задаётся следующим образом:
![]() (14)
(14)
где ![]() — ограничение на реализацию ординарного маршрута
— ограничение на реализацию ординарного маршрута ![]() по критерию
по критерию ![]() . Аналогичным образом определяются множества допустимости четных и нечетных маршрутов.
. Аналогичным образом определяются множества допустимости четных и нечетных маршрутов.
Для нахождения оптимального маршрута перевозки продукции каждого вида необходимо определить функции цели, причём для каждого типа маршрутов целевые функции выглядят по-разному. Для ординарных маршрутов ![]() функция цели примет вид:
функция цели примет вид:![]() (15)
(15)
где ![]() — ограничение, соответствующее критерию
— ограничение, соответствующее критерию ![]() ;
; ![]() — количество перевозок;
— количество перевозок; ![]() — вид продукции,
— вид продукции, ![]() — двойственные переменные задачи. Для нечётных маршрутов
— двойственные переменные задачи. Для нечётных маршрутов ![]() целевая функция определяется следующим образом:
целевая функция определяется следующим образом: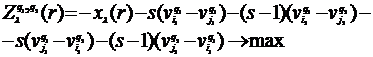 (16)
(16)
где ![]() — ограничение, соответствующее критерию
— ограничение, соответствующее критерию ![]() ;
; ![]() — количество перевозок;
— количество перевозок; ![]() — вид продукции,
— вид продукции, ![]() — двойственные переменные задачи. Для чётных маршрутов
— двойственные переменные задачи. Для чётных маршрутов ![]() целевая функция задаётся следующим образом:
целевая функция задаётся следующим образом: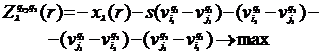 (17)
(17)
где ![]() — ограничение, соответствующее критерию
— ограничение, соответствующее критерию ![]() ;
; ![]() — количество перевозок;
— количество перевозок; ![]() — вид продукции,
— вид продукции, ![]() — двойственные переменные задачи.
— двойственные переменные задачи.
Таким образом, благодаря методу генерации маршрутов столбцов каждого типа возможен переход от громоздкой производственно-транспортной матрицы к матрице, состоящей из столбцов ординарных, четных и нечетных маршрутов. После чего возможно использование модифицированного симплексного метода, который приводит к решению производственно-транспортной задачи.
Разработана математическая модель генерации столбцов наиболее эффективных замкнутых маршрутов для перевозки лесоматериалов от лесозаготовительных предприятий к лесоперерабатывающим, оптимизирующая грузопотоки с помощью разбиения лесотранспортной сети на множество графов, в каждом из которых производится перевозка лишь одного вида продукции.
В данной модели маршрут ![]() характеризуется списком, состоящим из пунктов рубки
характеризуется списком, состоящим из пунктов рубки ![]() , пунктов потребления
, пунктов потребления ![]() , вида лесосырья
, вида лесосырья ![]() , а также эффективностью и временем, затраченным на перевозку:
, а также эффективностью и временем, затраченным на перевозку:![]() (18)
(18)
Таким образом, множество всевозможных маршрутов ![]() определяется следующим образом:
определяется следующим образом: ![]() (19)
(19)
Пусть ![]() — количество транспортных средств, выполняющих работу по маршруту
— количество транспортных средств, выполняющих работу по маршруту ![]() ;
; ![]() — максимальный объём производства продукции вида
— максимальный объём производства продукции вида ![]() в пункте производства
в пункте производства ![]() ;
; ![]() — минимальный объём потребления продукции вида
— минимальный объём потребления продукции вида ![]() в пункте потребления
в пункте потребления ![]() . Тогда суммарный объём вывезенной из узла
. Тогда суммарный объём вывезенной из узла ![]() продукции вида
продукции вида ![]() не должен превышать максимального значения:
не должен превышать максимального значения:![]() (20)
(20)
Объём ввезённой в узел ![]() продукции вида
продукции вида ![]() не должен превосходить минимально допустимый:
не должен превосходить минимально допустимый:![]() (21)
(21)
Тогда задача генерации маршрутов примет вид: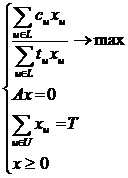 (22)
(22)
Транспортная сеть задачи, представленная графом ![]() , может быть разбита на множество транспортных сетей перевозок продукции:
, может быть разбита на множество транспортных сетей перевозок продукции:
![]()
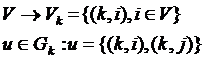 (23)
(23)

Рис.1 Маршрут перевозки продукции ![]() , изображенный в виде цилиндра.
, изображенный в виде цилиндра.
Таким образом, оптимизация грузопотоков происходит с помощью разбиения лесотранспортной сети на множество графов, в каждом из которых рассматривается и производится перевозка лишь одного вида продукции.
В результате исследований разработаны и апробированы три взаимоувязанные математические модели, оптимизирующие процесс транспортировки лесоматериалов в рамках территориально распределённых лесозаготовительных и лесоперерабатывающих предприятий лесопромышленного региона:
- математическая модель управления производственными мощностями лесотранспортного предприятия;
- математическая модель оптимизации парка машин лесозаготовительного предприятия, интегрированного в лесоперерабатывающий холдинг;
- математическая модель генерации столбцов наиболее эффективных замкнутых маршрутов для перевозки лесоматериалов от лесозаготовительных предприятий к лесоперерабатывающим.
Результаты исследований являются научной основой для принятия стратегических и тактических решений по формированию грузопотоков в лесопромышленном регионе. Разработанный программный комплекс, являющийся реализацией разработанных математических моделей по оптимизации перевозок лесоматериалов, применим для решения прикладных производственно-транспортных задач лесопромышленных предприятий, интегрированных в лесоперерабатывающий холдинг.
Литература:
1.Воронин А. В., Шегельман И. Р. Лесопромышленная интеграция: теория и практика. Петрозаводск, Изд-во ПетрГУ, 2009. 464 c.
2.Шегельман И. Р. К вопросу формирования отечественной технологической платформы развития лесного сектора России / И. Р. Шегельман, М. Н. Рудаков // Глобальный научный потенциал. – 2011. – № 9. – С. 104-107.
3.Вывозка леса автопоездами / И. Р. Шегельман, Скрыпник В. И., Кузнецов А. В., Пладов А. В.; СПб: ПРОФИКC, 2008. 304 с.
4.Моделирование движения лесовозных автопоездов на ПЭВМ / Шегельман И. Р., Скрыпник В. И., Пладов А. В., Кочанов А. Н., Кузнецов В. А.. Петрозаводск: ПетрГУ, 2003. 234 с.
5.Шегельман И. Р. Лесная промышленность и лесное хозяйство: Словарь / авт.-сост. И. Р. Шегельман. 5-е изд., перереб. и доп. Петрозаводск, Изд-во ПетрГУ, 2011. – 328 с.
6.Шегельман И. Р. Эффективная организация автомобильного транспорта леса: / И. Р. Шегельман, В. И. Скрыпник, А. В. Кузнецов. Петрозаводск, Изд-во ПетрГУ, 2007. 288 c.
7.Оптимизация в планировании и управлении предприятиями регионального лесопромышленного комплекса / Булатов А. Ф., Воронин А. В., Кузнецов В. А., Пладов В. А., Шегельман И. Р. Петрозаводск: ПетрГУ, 2001. 228 с.
8.Теория и практика принятия оптимальных решений для предприятий лесопромышленного комплекса/ А. В. Воронин, В. А. Кузнецов, И. Р. Шегельман, Л. В. Щеголева. – Петрозаводск: Изд-во ПетрГУ, 2008. – 180.