Описание потенциальной функции для уточненного уравнения линий тока
Аннотация
Дата поступления статьи: 27.06.2013В настоящей работе предлагается уточненное описание потенциальной функции при свободном растекании бурного стационарного двухмерного планового потока. В отличии от предыдущего решения, новое удовлетворяет условиям неразрывности параметров течения при выходе потока из прямоугольной трубы в отводящее русло.
Ключевые слова: крайняя линия тока, эквипотенциали, прямоугольная труба, горизонтальное отводящее русло
Определение параметров свободного растекания потока за водопропускными отверстиями в широкое отводящее русло имеет важное прикладное значение для проектирования сооружений дорожного водоотвода. При этом полагают дно отводящего русла горизонтальным, а поток двухмерным в плане.
В работах [1, 2, 3] показано, что силами сопротивления потоку в области крепления отводящего русла можно пренебречь. Поэтому дополнительно полагаем поток потенциальным и стационарным. Выводы применимости полученного результата сделаем по степени адекватности модели и реального потока по его параметрам.
Рассмотрим схему течения потока в плане.
Рисунок 1 – План растекания потока в терминах линия тока, эквипотенциаль
Для формулировки задачи в физической плоскости течения сформулируем свойства бурного потока. Известны параметры 
на выходе потока из прямоугольного безнапорного отверстия в широкое отводящее русло:
глубина потока;
модуль вектора скорости;
ширина выходного отверстия.
Перейдем от физической плоскости течения потока [4, 5] к использованию уравнений движения потока в плоскости годографа скорости. Система уравнений движения потока в плоскости годографа скорости представлена в форме [6]:
(1)
где: 
потенциальная функция;
функция тока;
угол между вектором скорости жидкой частицы потока и осью ОХ;
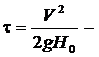нормированный модуль вектора скорости.
В работе [7] получено уравнение крайней линии тока в виде
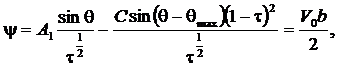(2)
где: 
Найдем уравнение для произвольной эквипотенциали. Воспользуемся сначала первым уравнением из (1). Для этого найдем из (2)
(3)
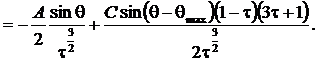
Подставим выражение (3) в первое уравнение системы (1), получим уравнение
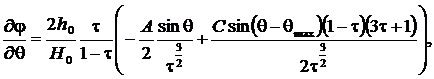
или
(4)
Интегрирование уравнения (4) по переменной 
приводит к зависимости
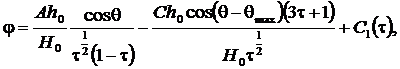(5)
где 
неизвестная функция по переменной 
.
Для нахождения 
воспользуемся вторым уравнением системы (1).
Вычисляем производную по 
от потенциальной функции 
в форме (5)
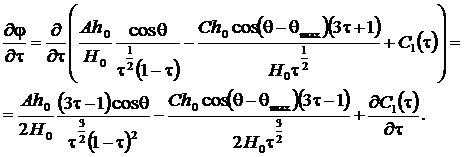(6)
Найдем производную 
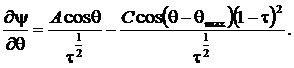(7)
Подставим выражения (6) и (7) во второе уравнение системы (1), получим
(8)
Нетрудно видеть, что после упрощений уравнение (8) преобразуется к виду
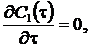
или 
(9)
Таким образом, искомое выражение для потенциальной функции имеет вид
(10)
Функция (10) является решением уравнения (1) при любом значении постоянной 
, в частности, при 
Значение константы 
может быть определено в конкретной двухмерной плановой задаче.
Изучим поведение каждого из слагаемых, входящих в выражение для потенциальной функции. Пусть 
Представим потенциальную функцию в форме
(11)
где: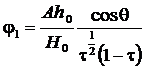 
; 
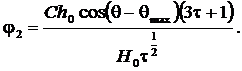
Рассмотрим отношение
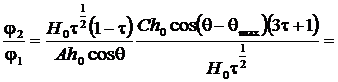
(12)
Найдем значение величины 
(13)
Упростим правую часть равенства (12)
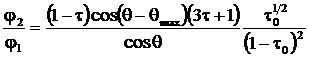(14)
Как известно из [1], вниз по течению потока 
, соответственно в выражении 
, что нетрудно видеть из (14), числитель стремится к нулю, а знаменатель всегда отличен от нуля. Таким образом,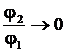 
при 
, то есть вниз по течению потока в формуле (11) влияние первого слагаемого становится преобладающим.
Плановые задачи гидравлики решаются также и численными методами [8, 9, 10], однако аналитические методы решения двухмерных плановых задач позволяют более глубоко и всесторонне изучить свойства двухмерных бурных потоков.
Выводы по работе.
- Выражение для потенциальной функции в виде (11) соответствует качественно и количественно экспериментальным данным (неразрывности по параметрам потока, адекватности модели).
- Роль слагаемого
в выражении (11) асимптотически уменьшается с ростом 
вниз по течению потока.
Литература:
1. Коханенко, В.Н. Моделирование одномерных и двухмерных открытых водных потоков [Текст]: монография / В.Н. Коханенко, Я.В. Волосухин, В.В. Ширяев, Н.В. Коханенко; под общей ред. В.Н. Коханенко. – Ростов н/Д: Изд-во ЮФУ, 2007. – 168 с.
2. Ширяев, В.В. Развитие теории двухмерных открытых водных потоков [Текст]: монография / В.В. Ширяев, М.Ф. Мицик, Е.В. Дуванская: под общей ред. В.В. Ширяева. – Шахты: Изд-во ЮРГУЭС, 2007. – 133 с.
3. Takeda, R. Theoretical research an propeller type current meters [Текст] / R. Takeda // Trans. ASME. – 1975, A. 97, № 4. – Р. 599-602.
4. Мицик, М.Ф. Моделирование потенциальной функции двухмерного планового потока в параметрической форме [Текст] // Математические методы в технике и технологиях: Сб. тр. VI межд. науч. конф. / Под общей ред. В.С. Балакирева. – РТАСМ ГОУ, Ростов н/Д, 2003. – Т. 7, секция 7. – С. 103-104.
5. Мицик, М.Ф. Растекание двухмерного планового потока в нижнем бьефе водопропускных сооружений [Текст]: дисс. на соиск. уч. степ. канд. техн. наук. – Новочеркасск, 2006. – 238 с.
6. Косиченко, Н.В. Анализ изучения и уточнения методов свободного растекания потока за безнапорными водопропускными отверстиями [Текст] / Н.В. Косиченко // Вестник СГАУ. – Саратов, 2011, № 9. – С. 27-33.
7. Коханенко В.Н., Мицик М.Ф., Косиченко Н.В. Уточненное уравнении крайней линии тока в плоскости годографа скорости в задаче свободного растекания бурного потока за безнапорными водопропускными трубами // Изв. вузов. Сев.-Кавк. регион. Техн. науки. 2013. №1. С. 33-35.
8. Takeda, R. The influence of turbulence on the characteristic of the propeller current meters [Текст] / R. Takeda, M. Kawanami // Trans. Soc. Mtch. Eng.– 1978, № 383. – V. 44. – P. 2389- 2394.
9. Онишкова А.М. Численное решение задачи для плоской области со свободной границей. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4p1y2012/1205 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Хекмат К. Двумерная математическая модель жидкости водоема с учетом наличии на поверхности ледяной пластины [Электронный ресурс] // «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2011/583 (доступ свободный) – Загл. с экрана. – Яз. рус.