Расчетная модель гидродинамической смазки неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения при наличии принудительной подачи смазки
Аннотация
Дата поступления статьи: 08.08.2013С целью исследования устойчивости работы пористых подшипников разработана расчетная модель неоднородного пористого подшипника конечной длины. С учетом анизотропии проницаемости пористого слоя в работе рассмотрены задачи об устойчивости движения шипа в подшипнике для двух разных вариантов подачи смазки: в осевом направлении и в направлении, перпендикулярном оси подшипника. Получены и проанализированы решения задач, определены области устойчивости движения шипа.
Ключевые слова: пористый подшипник, режим трения, проницаемость пористого слоя, вязкоупругая смазка.
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Задача об устойчивости работы однослойных и двухслойных пористых подшипников конечной длины рассматривались в работах [1-7]. Существенным недостатком указанных работ является то, что в них проницаемость пористых слоев считается постоянной и, кроме того, не учитывается источник подачи смазки (рис. 1). В рассматриваемом случае трудно обеспечить жидкостный режим трения, так как подшипник работает за счет запаса смазки лишь в порах пористого слоя.
В настоящей работе нами, с учетом анизотропии проницаемости пористого слоя и наличия принудительной подачи смазки, приводится расчетная модель неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения. Здесь вначале рассматривается случай, когда смазка принудительно подается в направлении оси Oy, а затем в осевом направлении. Проницаемость задается в виде (1) (рис.1):
![]() . (1)
. (1)
Здесь A – заданная постоянная величина; H– толщина пористого слоя; l– безразмерный параметр, характеризующий распределение проницаемости в направлении оси Oy.
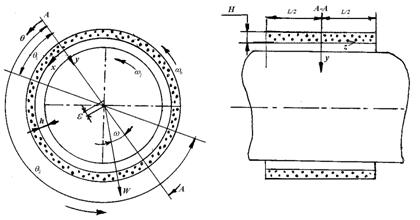
Рис. 1. Радиальный подшипник конечной длины с пористой обоймой
Гидродинамический расчет рассматриваемого подшипника нами будет производиться при следующих допущениях [1,2].
1. Толщина пористого слоя считается малой по сравнению с радиусом подшипника и в конечной модели используется короткий подшипник. Уравнение, определяющее течение смазки, в пористой матрице представляется в виде
![]() , (2)
, (2)
где y, z – прямоугольные координаты (рис.1), ![]() – гидродинамическое давление в пористом слое.
– гидродинамическое давление в пористом слое.
2. Для определения распределения давления в пленке смазки между шипом и подшипником будем исходить из модифицированного уравнения Рейнольдса в рамках модели короткого подшипника [1] .
![]() , (3)
, (3)
где ![]() – толщина пленки смазки, C – радиальный зазор, e – относительный эксцентриситет, q – угловая координата, p – давление в пленке смазки, m – динамический коэффициент вязкости,
– толщина пленки смазки, C – радиальный зазор, e – относительный эксцентриситет, q – угловая координата, p – давление в пленке смазки, m – динамический коэффициент вязкости, ![]() – угловые скорости соответственно подшипника, шипа и нагрузки, j – угол положения, t – время,
– угловые скорости соответственно подшипника, шипа и нагрузки, j – угол положения, t – время, ![]() – компонента скорости в направлении y на внутренней границе пористого слоя, прилегающая к зазору:
– компонента скорости в направлении y на внутренней границе пористого слоя, прилегающая к зазору:
 , (4)
, (4)
где ![]() – проницаемость материала пористого слоя.
– проницаемость материала пористого слоя.
Система уравнений (2)-(3) в случае подачи смазки через поры пористого слоя в направлении оси Oy решается при граничных условиях (рис. 1)
![]() при
при ![]() ;
; ![]() при
при ![]() ;
;
![]() при
при ![]() ;
; ![]() при
при ![]() (5)
(5)
где ![]() – скорость подачи смазки,
– скорость подачи смазки, ![]() – атмосферное давление.
– атмосферное давление.
В случае подачи смазки в осевом направлении граничные условия запишутся в следующем виде (рис.2, начало координат в этом случае выбрано в левом конце подшипника)
![]() при
при ![]() ;
; ![]() при
при ![]() ;
;
![]() при
при ![]() ;
; ![]() при
при ![]() . (6)
. (6)
Здесь ![]() – давление в начальном сечении;
– давление в начальном сечении; ![]() – в конечном сечении.
– в конечном сечении.
Переход к безразмерным переменным.
В дальнейшем предполагается, что ![]() .
.
Перейдем к безразмерным величинам по формулам [1]:
![]() . (7)
. (7)
Тогда уравнения (2) и (3) принимают следующий вид:
![]() ; (8)
; (8)
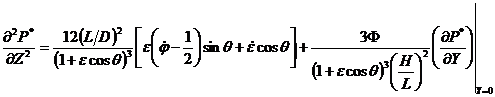 , (9)
, (9)
где ![]() ; точкой обозначено дифференцирование по T.
; точкой обозначено дифференцирование по T.
Граничные условия (5) и (6), соответственно, примут следующий вид
![]() при
при ![]() ;
; ![]() при
при ![]() ;
;
![]() при
при ![]() ;
; ![]() при
при ![]() ; (10)
; (10)
![]() при
при ![]() ;
; ![]() при
при ![]() ;
;
![]() при
при ![]() ;
; ![]() при
при ![]() , (11)
, (11)
где ![]() .
.
Перейдем к решению системы (8)-(9) с граничными условиями (10).
Установим закон подачи смазки в виде
![]() (12)
(12)
Полагая толщину пористого слоя малой, уравнение (8) осредним по толщине смазочного слоя. Тогда уравнение (8) запишется в виде
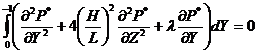 . (13)
. (13)
Решение уравнения (13), удовлетворяющее граничным условиям (10), будем искать в виде
![]() . (14)
. (14)
Подставляя (14) в (13), приходим к следующему уравнению
![]() . (15)
. (15)
Выполняя граничные условия (10), будем иметь:
![]() ,
, ![]() ,
,
![]() . (16)
. (16)
Решение уравнения (16) можно найти после определения функции ![]() , удовлетворяющей условию
, удовлетворяющей условию
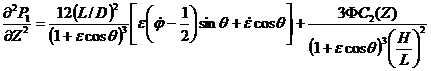 . (17)
. (17)
Уравнение решается при граничных условиях
![]() при
при ![]() (18)
(18)
Полагая ![]() , с учетом граничных условий (18), для
, с учетом граничных условий (18), для ![]() окончательно получим следующее выражение
окончательно получим следующее выражение
 . (19)
. (19)
С учетом (19), уравнение (16) решается при граничных условиях
![]() при
при ![]() .
.
При определении основных рабочих характеристик явный вид функций ![]() и
и ![]() нам не понадобятся.
нам не понадобятся.
Перейдем к случаю осевой подачи смазки (рис. 2).
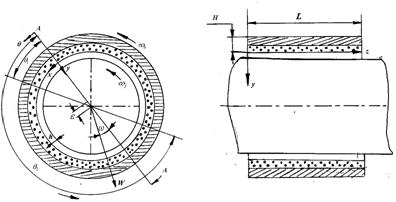
Рис. 2. Радиальный подшипник конечной длины с двухслойной пористой обоймой
Решение уравнений (9) и (13), удовлетворяющих граничным условиям (11), будем искать в виде
![]() ,
, ![]() . (20)
. (20)
С учетом граничных условий (11), для определения ![]() приходим к следующему уравнению
приходим к следующему уравнению
![]() . (21)
. (21)
Функции ![]() и
и ![]() выражаются через функцию
выражаются через функцию ![]() в виде
в виде
![]() ,
, ![]() . (22)
. (22)
Константы ![]() и
и ![]() определяются выражениями
определяются выражениями
![]() ,
, ![]() (23)
(23)
Решая уравнение (21) с граничными условиями ![]() ,
, ![]() при
при ![]() ,
, ![]() , для
, для ![]() получим следующее выражение
получим следующее выражение
![]() . (24)
. (24)
С учетом (24), для определения уравнения ![]() приходим к следующему уравнению
приходим к следующему уравнению
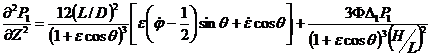 . (25)
. (25)
Решая уравнение (25) с граничными условиями ![]() при
при ![]() ,
, ![]() , для
, для ![]() окончательно получим следующее выражение
окончательно получим следующее выражение
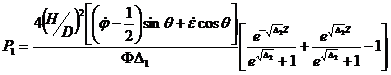 , (26)
, (26)
где 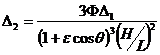 ,
, ![]() .
.
Перейдем к определению усилий масляной пленки.
При неполном заполнении смазкой зазора область положительных давлений, ограниченная углами ![]() и
и ![]() , определяются из условий
, определяются из условий
![]() ;
;
![]() ,
, ![]() .
.
В случае подачи смазки в направлении перпендикулярной оси подшипника через поры пористого слоя с заданной скоростью, усилия масляной пленки вычисляются интегрированием по положительной области распределения давления, определяемые формулой
 (27)
(27)
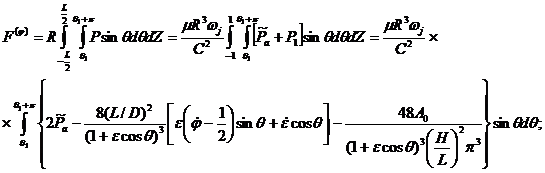 (28)
(28)
В случае осевой модели смазки
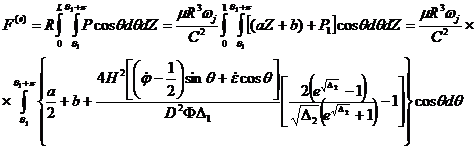 . (29)
. (29)
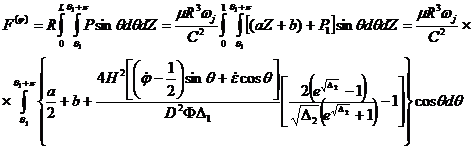 . (30)
. (30)
В случае полного заполнения смазкой зазора и подачи смазки в направлении оси Oy будем иметь
 ;(31)
;(31)
 . (32)
. (32)
Рассмотрим случай полного заполнения смазкой зазора и осевой подачи смазки. Используя формулу (26), будем иметь
 ; (33)
; (33)
 . (34)
. (34)
Решение задачи на устойчивость
Безразмерные уравнения, определяющие движение шипа, записываются в следующем виде
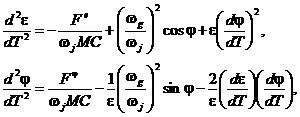 (35)
(35)
где ![]() – масса ротора.
– масса ротора.
![]() и
и ![]() – усилия масляной пленки, в случае неполного заполнения смазкой зазора они определяются формулами (27), (28), когда смазка подается перпендикулярно оси подшипника, и формулами (29) и (30) в случае осевой подачи смазки. Для случая полного заполнения смазкой зазора эти усилия определяются, соответственно, формулами (31)-(34).
– усилия масляной пленки, в случае неполного заполнения смазкой зазора они определяются формулами (27), (28), когда смазка подается перпендикулярно оси подшипника, и формулами (29) и (30) в случае осевой подачи смазки. Для случая полного заполнения смазкой зазора эти усилия определяются, соответственно, формулами (31)-(34).
Уравнения (35), определяющие движение шипа, решаются численно с учетом полученных данных (27)-(34). Компоненты ускорения ![]() ,
, ![]() представляют собой явные функции параметров
представляют собой явные функции параметров ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнения (31) записываются в стандартной форме первого порядка и решаются с помощью метода, разработанного Гиром [7].
После получения решения уравнений движения, устойчивость рассматриваемого движения определяется визуально по графику. При заданных значениях выше указанных параметров, области устойчивости приведены на рис. 3-4. Здесь все точки, которые лежат ниже кривых устойчивости, соответствуют устойчивому движению шипа, а все точки, которые лежат выше кривых, соответствуют неустойчивому движению ![]() , где
, где ![]() – ускорение силы тяжести.
– ускорение силы тяжести.
Из зависимостей, приведенных на рис. 3 и 4, следует, что:
1. Пористый подшипник как при осевой подаче смазки, так и при подаче перпендикулярно оси, работает более устойчиво, чем пористый подшипник, работающий без подачи смазки.
2. Площадь области устойчивости, в случае подачи смазки в направлении перпендикулярной оси подшипника, расширяется в сравнении с подачей смазки в осевом направлении.
3. В случае полного заполнения смазкой зазора и учета анизотропии проницаемости пористого слоя подшипник работает более устойчиво, чем при частичном заполнении смазкой зазора и при ![]() .
.

Рис. 3. Схематическое изображение границ области устойчивости.
Подача смазки в направлении оси Оy (![]() )
)
1 - ![]() =0,03,
=0,03, ![]() =0,1; 2 -
=0,1; 2 - ![]() =0,03,
=0,03, ![]() =0;
=0;
3 - ![]() =0,03,
=0,03, ![]() =0,1 (неполное заполнение смазкой зазора);
=0,1 (неполное заполнение смазкой зазора);
4 - ![]() =0,03,
=0,03, ![]() =0 (неполное заполнение смазкой зазора);
=0 (неполное заполнение смазкой зазора);
5 - ![]() =0,01,
=0,01, ![]() =0,1; 6 -
=0,1; 6 - ![]() =0,
=0, ![]() =0;
=0;
7 - ![]() =0,01,
=0,01, ![]() =0,1 (неполное заполнение смазкой зазора);
=0,1 (неполное заполнение смазкой зазора);
8 - ![]() =0,01,
=0,01, ![]() =0 (неполное заполнение смазкой зазора).
=0 (неполное заполнение смазкой зазора).
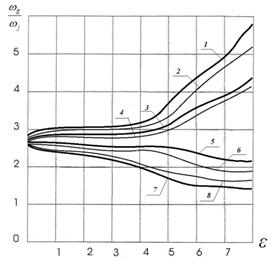
Рис. 4. Схематическое изображение границ области устойчивости
Осевая подача смазки (![]() =0,04;
=0,04; ![]() =0,03;
=0,03; ![]() =0,5;
=0,5; ![]() =0)
=0)
1 - ![]() =0,03,
=0,03, ![]() =0,1; 2 -
=0,1; 2 - ![]() =0,03,
=0,03, ![]() =0;
=0;
3 - ![]() =0,03,
=0,03, ![]() =0,1 (неполное заполнение смазкой зазора);
=0,1 (неполное заполнение смазкой зазора);
4 - ![]() =0,03,
=0,03, ![]() =0 (неполное заполнение смазкой зазора);
=0 (неполное заполнение смазкой зазора);
5 - ![]() =0,01,
=0,01, ![]() =0,1; 6 -
=0,1; 6 - ![]() =0,
=0, ![]() =0;
=0;
7 - ![]() =0,01,
=0,01, ![]() =0,1 (неполное заполнение смазкой зазора);
=0,1 (неполное заполнение смазкой зазора);
8 - ![]() =0,01,
=0,01, ![]() =0 (неполное заполнение смазкой зазора).
=0 (неполное заполнение смазкой зазора).
Литература:
1. Конри. Об устойчивости пористых радиальных подшипников. Конструирование и технология машиностроения / Конри, Кузано // Вестник Машиностроения.- 1974. - № 2. - С. 206-216.
2. Ахвердиев, К.С.,Об устойчивости двухслойных пористых радиальных подшипников / К.С. Ахвердиев, О.В. Муленко // Вестник РГУПС. - 2002. - № 3. – С. 5-7.
3. Кузано. Исследование коэффициента передачи упругой опоры качения в демпфере со сдавливаемой пленкой и пористой обоймой. / Кузано, Р.Е. Франк // Проблемы трения и смазки. - изд-во «Мир». – 1974. - № 1, - С. 54.
4. Ахвердиев, К.С. Разработка математической модели гидродинамического расчета конических подшипников. / К.С. Ахвердиев, Б.Е. Копотун // – Вестник РГУПС. - 2005. - № 3. - С 5-9.
5. Ахвердиев, К.С. Нестационарная математическая модель гидродинамической смазки сложнонагруженного составного конического подшипника с пористым слоем на его рабочей поверхности с учетом его конструктивной особенности. / К.С. Ахвердиев, С.Ф. Кочетова, М.А. Мукутадзе // - Вестник РГУПС. - 2009 - № 1. – С. 135-143.
6. Ахвердиев, К.С. Устойчивость движения шипа в коническом подшипнике с пористым слоем на рабочей поверхности. / К.С. Ахвердиев, Б.Е. Копотун, М.А. Мукутадзе // - Трение и износ. – 2007. – Т. 28. - № 4. – С. 361-366.
7. Gear C.W., Numarical Initial Value Problems in Ordinary Differential Equations / C.W. Gear. - Prentice-Hall, Inc., Englewood Cliffs. - N.J., 1972. – С. 52.
8. Майба, И.А., Глазунов, Д.В. Теоретическое обоснование механизма смешанной (полужидкостной) смазки в контакте «твердый оболочечный смазочный стержень-колесо-рельс» [Электронный ресурс] // «Инженерный вестник Дона», 2012 г., №1 – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/664 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Дерлугян Ф.П., Щербаков И.Н. Обоснование процесса получения композиционных антифрикционных самосмазывающихся материалов с заданными техническими характеристиками методом химического наноконструирования. [Электронный ресурс] // «Инженерный вестник Дона», 2010 г., №4 – Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/287 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp Tower”s experiments / O. Reynolds. – Phil. Trans. Roy. Soc. London, 1886, vol. 177, pt. 1.