Моделирование электродинамических параметров двухзазорного клистронного резонатора

Аннотация

А.Ю. Мирошниченко, В.А. Царев

Дата поступления статьи: 19.08.2013

В статье рассмотрены двухзазорные цилиндрические резонаторы с противофазным возбуждением, которые находят широкое применение в конструкциях пролетных усилительных клистронов. Одним из путей уменьшения времени при машинном проектировании клистронных резонаторов является использование простых аналитических соотношений, позволяющих с достаточной для практики точностью, оперативно определять основные электродинамические параметры. В работе проведено физическое и математическое моделирование двухзазорного резонатора, предложены уточненные математические модели, которые могут найти применение в программах оперативной оптимизации СВЧ приборов клистронного типа. Проведенный анализ адекватности полученных моделей показал, что в выбранных диапазонах изменения влияющих факторов погрешности расчета резонансной частоты противофазного вида колебаний не превышают 1%, характеристического сопротивления - 5%. Полученные аналитические соотношения позволяют оперативно провести расчет параметров резонатора, не прибегая к трудоемким и дорогостоящим экспериментам и расчетам.

Ключевые слова: двухзазорный резонатор, электродинамические параметры, математическое моделирование, резонансная частота, характеристическое сопротивление, метод планируемого эксперимента.

05.12.07 - Антенны, СВЧ устройства и их технологии

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Введение

В последнее время в конструкциях пролетных усилительных клистронов длинноволнового и средневолнового диапазонов частот находят все большее применение двухзазорные цилиндрические  резонаторы с противофазным возбуждением, которые позволяют расширить полосу усиления,  а также увеличить  коэффициент усиления и КПД этих приборов [1,2]. 
Однако такие электродинамические системы более трудоемки в разработке, по сравнению с обычными однозазорными резонаторами, поскольку они не имеют аксиальной симметрии, а для получения заданных электродинамических характеристик клистрона требуют подбора  большего числа геометрических  параметров.Оптимальные размеры этих резонаторов приходится  подбирать  либо экспериментально,  либо расчетным путем.
Применение программ точного моделирования трехмерных электродинамических структур - это новыйподход, которыйиграет важную роль в процессе проектирования электронных приборов и устройств СВЧ [3-5].Разработанныепрограммы строгого трехмерного  численного расчета резонаторов, такие как CST MICROWAVE STUDIO и HFSS вычисляют многомодовые S-параметры и электромагнитные поля для трехмерной электродинамической системы произвольной формы. Их применение заменяет традиционное макетирование  резонаторов методом «проб и ошибок», улучшая качество проектирования. Однако процесс  машинного проектирования, так же как и эксперимент,  чрезвычайно трудоемкий. К тому же, не всегда удается найти связь между S-параметрами и основными электродинамическими параметрами характеристиками резонаторов, такими, например, как емкость резонатора и характеристическое сопротивление(где- эквивалентное сопротивление резонатора, - собственная добротность). Одним из путей уменьшения времени при машинном проектировании  резонаторов является использование простых аналитических соотношений, позволяющих с достаточной для практики точностью, оперативно определять основные электродинамические параметры. Эти соотношения  в большинстве случаев состоят из аналитических зависимостей, дополненных  аппроксимацией эмпирических кривых или эмпирических формул[6, 7].
Так как в настоящее время отсутствуют адекватные  приближенные математические модели двухзазорного резонатора, то физическое и математическое  моделирование этой электродинамической системы с целью построения удовлетворительной математической модели для расчета основных параметров двухзазорного резонатора является актуальной задачей.

1 Методика аналитического расчета резонансной частоты и характеристического сопротивления

В работе исследуется двухзазорный резонатор с возбуждением на противофазном виде колебаний. Конструктивная схема с указанием основных размеров и характер распределения ВЧ поля в зазорах резонатора показаны на рис.1.
Эквивалентная электрическая схема двухзазорного резонатора, возбуждаемого на -виде колебаний  может быть представлена в виде параллельного L₀C₀ контура, резонансную частоту ω0 которого получим из  условия равенства реактивных проводимостей B_Cи B_Lотрезка полосковой

Рис. 1. - Схема исследуемого резонатора линии, закороченной на одном конце и, нагруженной на емкость двойного зазора на другом конце [8]

,               (1)
где С₀− сосредоточенная ёмкость на конце линии (емкость двойного зазора); l-длина полосковой линии, образованной боковыми крышками и центральным проводником;с− фазовая скорость волны типа ТЕМ в линии, равная, в случаевакуумного наполнения, скорости света; Z₀-волновое сопротивление полосковой линии:
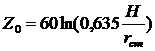,    (2)
где H- высота резонатора;r_ст- радиус центрального проводника (стержня) резонатора.
Характеристическое сопротивление резонатора ρв значительноймере влияет на такие параметры клистрона как полный КПД, полоса иусиление. По этой причине при расчете и проектировании СВЧ приборов клистронного типа необходимо знать, по возможности, более точное значение ρ.
Приближенный аналитический расчет характеристического  сопротивления двухзазорного резонатора в большинстве случаев производится по формуле [9]
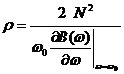      (3)
Из  уравнений  (1) и (3)  можно получить следующее  выражение
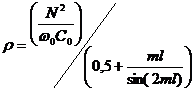,      (4)
где  - приведенная длина резонансной линии, N – число зазоров.
Таким образом, зная точные значения емкости двойного зазора C₀  и параметры эквивалентной длинной линии l и z₀ можно аналитически рассчитать резонансную частоту  и величину характеристического сопротивления резонатора.

2Аналитический метод расчета эквивалентной емкости двойного бессеточного зазора

Задача о нахождении емкости бессеточных зазоров клистронного резонатора решалась и ранее [10], но правильность применения предложенных приближенных формул для расчета двухзазорного резонатора не была подтверждена надежными экспериментальными данными  или строгими электродинамическими расчетами. 
Емкость одиночного бессеточного зазора  С₁обычно рассчитывается как сумма торцевой емкости СТ и «внутренней емкости» С_вн, для расчета которой вводится  - коэффициент, учитывающий уменьшение торцевой емкости бессеточного зазора по сравнению с сеточным
,
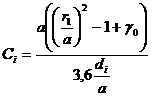где d_i- длина зазора; i – номер зазора, i=1,2;r₁- внешний радиус пролетных труб; a - радиус пролетного канала.
Для двухзазорного резонатора  в случае несимметричных зазоров  полную емкость зазора С0 можно представить как сумму двух торцевых емкостей С₁, C₂ и боковой емкости C_б со втулки на корпус резонатора
.    (5)
Торцевые емкости = можно определить следующим образом:
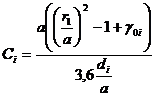,  (6)
При подстановке в эту формулу размеров резонатора всм, емкость C_i получается  впФ.Однако эта методика усложняет процесс проектирования резонатора и увеличивает его трудоемкость. Для вычисления коэффициента можно использовать в диапазоне отношений  следующие приближенные аналитические соотношения:
,   (7)
где  ;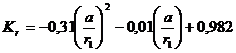
.
Боковую емкость Сб, входящую в выражение (5), можно рассчитать как емкость отрезка коаксиальной линии, образованной втулкой с длиной lвт  и внешним радиусом r₁  и корпусом резонатора с радиусом R
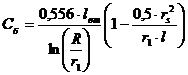   (8)
В формуле (8) учтена поправка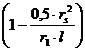, связанная с уменьшением  боковой емкости втулки за счет  экранировки ее стержнем с радиусомrs. Недостатком описанной выше методики является то, что  аппроксимация коэффициента проведена по данным аналитического расчета.
Однако проверка правильности этих  приближенных формул должна быть поддержана надежными экспериментальными данными  или строгими электродинамическими расчетами.

3 Определение эквивалентнойемкости двойногобессеточного зазора с помощью метода планируемого  эксперимента

Методика построения приближенной математической модели в этом случае сводилась к определению опорной аналитической функции, и последующей аппроксимации  невязки между экспериментальными и расчетными данными с помощью метода планируемого эксперимента.
Для проведения исследований по методике планируемого  эксперимента необходимо было, согласно центральному композиционному плану [11] для трех безразмерных факторов (, , )провести 15 опытов с резонаторами,  размеры зазоров которых должны варьироваться в соответствии с планом эксперимента.  С этой целью был изготовлен специальный  разборный  макетрезонатора,  позволяющий  путем механической перестройки изменятьсоотношения между его основными  геометрическими размерами. Дляповышения точности измерений резонансных частот макет резонатора был выполнен в увеличенном размере, так что его резонансные частоты (при измененииразмеров зазоров) находились в диапазоне 400-600 МГц.
В качестве опорной аналитической функции,  описывающей емкость  C₁ была выбрана функция, описывающая емкость C₁₀ между двумя коаксиальными круговыми кольцами [12]
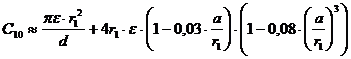        (9)
Полная емкость двойного зазора С₂₀ (опорная функция) при этом  определяетсяпо уравнению
   (10)
Для невязки между экспериментальными и расчетными данными  с помощью метода планируемого  эксперимента получено следующее выражение
,
где
Окончательно величина емкости рассчитывалась по формуле
       (11)

4 Методика экспериментального определения характеристического сопротивления

Перейдем теперь к методике экспериментального определения характеристического сопротивления ρ. В инженерной практике широко используется метод возмущения [13], согласно которому в канал помещают тонкую диэлектрическую ленту и прижимают ее  к  краю высокочастотного зазора,  перекрывая его. Определение  ρ  далее ведется по формуле:

      (12)
где f₀ - резонансная частота резонатора,  ГГц;d - длина  одного зазора в мм;N - число зазоров;–относительная диэлектрическая проницаемость диэлектрика;S-площадь поперечного сечения диэлектрика, мм²; - смещение частоты от внесения диэлектрика, МГц.
Приемлемая точность измерения ρ получается в том случае, если диэлектрическая лента тонкая , а зазор между трубами большой. Однако, при проведении экспериментов практически невозможно плотно прижать ленту по всей ширине к краю зазора, что приводит к разбросу    при  повторении  измерения и появлению ошибок.
В работе [14] приведена уточненная формула для расчета характеристического сопротивления многолучевого однозазорного резонатора, позволяющей рассчитывать ρ произвольных возмущениях.
Для двухзазорного резонатораэта формула может быть  переписана в виде
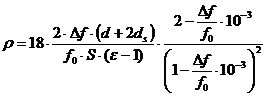,     (13)
где коэффициентучитывает провисание поля в канал.

5 Оценка точности полученных результатов

Результаты расчетов и измерений для одной точки плана, соответствующей параметрам, сведены в табл.1 и 2 и показаны на рис. 2 -4.
Таблица №1
Экспериментальные и расчетные значения резонансной частоты f, статической емкости C, двойного бессеточного зазора для параметров ,

Таблица №2
Экспериментальные и расчетные значения характеристического сопротивления двухзазорного  резонатора для параметров
,

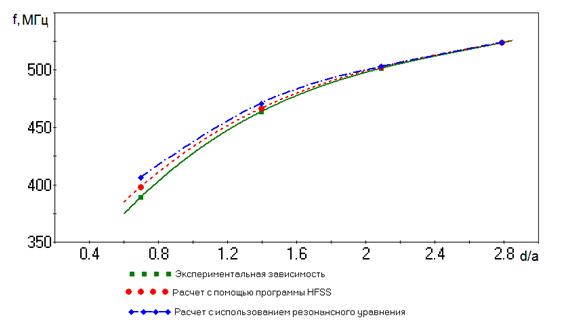
Рис. 2. - Зависимости частот резонатора от относительной длины зазора

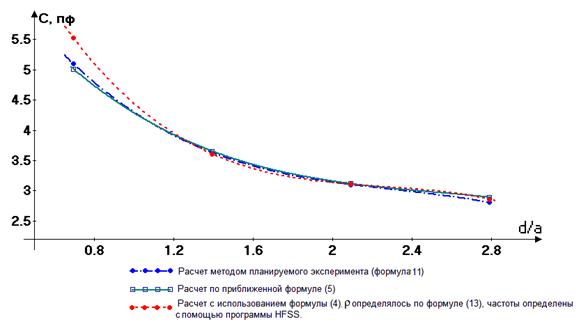
Рис.3. - Зависимости емкости резонатора от относительной длины зазора

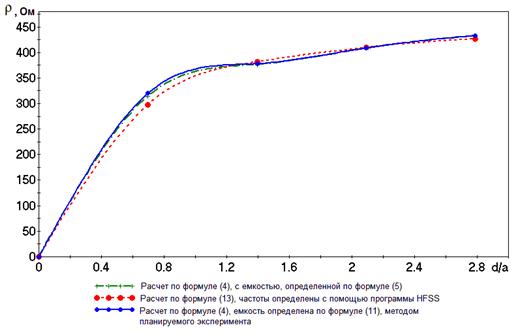
Рис. 3. - Зависимости характеристического сопротивления резонатора от относительной длины зазора

Анализ полученных результатов показывает, что погрешность определения резонансной частоты по уточненной формуле(11) (с корректирующим полиномом Y)меньше 1% в диапазоне изменения влияющих факторов:;   ;   .
Погрешность определения характеристического сопротивления по формуле (4) не превышает 5 % в диапазоне изменения влияющих факторов.
Однако, следует учесть, что экспериментальным путем, даже при большом наборе статистики, трудно определить ρ с погрешностью менее 5%. К сожалению, более строгие методы измерения ρ в настоящее время отсутствуют.

Выводы

1. Проведено физическое и математическое  моделирование двухзазорного резонатора, используемого в конструкциях пролетныхусилительных клистронов.
2. Предложены уточненные математические модели этой электродинамической системы, которые могут найти применение в программах оперативной оптимизации СВЧ приборов клистронного типа.
3. Проведенный анализ адекватности полученных моделей  показал, что в выбранных диапазонах изменения влияющих факторов погрешности расчета не превышают следующих значений:  резонансной  частоты противофазного вида  колебаний - 1%, характеристического сопротивления - 5%. Полученные  аналитические соотношения  позволяют оперативно провести расчет параметров резонатора, не прибегая к трудоемким  и  дорогостоящим  экспериментам  и расчетам.

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение № 14.B37.21.0909 «Исследование физических процессов в мощных многолучевых СВЧ электровакуумных приборах с электродинамическими системами, выполненными на основе многомодовых резонаторов»

Литература:

1.Shin,Ki R.Double-gap rebuncher cavity design of SNS MEBT / Ki R. Shin, Yoon W. Kang, Aly E. Fathy// Proceedings of International Particle Accelerator Conference and Exhibition. - New Orleans, USA – 2012. –Р. 3898-3900.
2.Lin, Fu-Min. Analysis of the optimal gap width and gap-to-gap distance in ¼-mode double-gap cavities for broadband klystrons / Fu-MinLin //Proceedings of Progress in electromagnetics research symposium. - Hangzhou, China. – 2008. –P. 1353-1356.
3.Банков,С.Е.Расчет антенни СВЧ структур с помощью HFSSAnsoft[Текст] / С.Е.Банков,А.А. Курушин. – М.:ЗАО «НПП «РОДНИК», 2009. - 256 с.
4.Шурховецкий, А.Н. Многоканальная частотно-избирательная система СВЧ диапазона на основе направленных фильтров бегущей волны[Электронный ресурс]  /  А.Н. Шурховецкий //Инженерный вестник Дона. – 2010. - №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/292 (доступ свободный) – Загл. с экрана. – Яз.рус.
5. Самарский, С.Г. Широкополосный печатный излучатель для фар различного назначения [Электронный ресурс] / С.Г. Самарский // Инженерный вестник Дона. – 2010. - №4. -Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/291 (доступ свободный) – Загл. с экрана. – Яз.рус.
6. Шатилов, В.С. Приближенный расчет параметров тороидальных ре­зонаторов[Текст]/В.С. Шатилов // Электронная техника.  Сер.1.  Электроника СВЧ.-1981.- Вып.3.- С. 34-38.
7. Оценка точности аналитических соотношений для расчета харак­теристик тороидальных резонаторов[Текст]/А.Н. Варнавский, Р.Ф. Дроздов, С.В.Королев, В.С.Шатилов // Электронная техника.Сер.1. Электроника СВЧ.- 1981.- Вып.11.- С. 28-30.
8.Орлов, С.И.Расчет и конструирование коаксиальных резонаторов [Текст] / С.И. Орлов. - М.: Сов.радио,1970.- 256 с.
9.Голубев, С.Н. Многорезонаторный пролетный усилительный клистрон [Текст]/ С.Н. Голубев, И.И. Лошакова, В.А. Царев. – Саратов:Сарат. политехн. ин-т, 1984.- 59 с.
10. Петров, Д.М. О «внутренней» емкости между торцами одинаковых труб[Текст]/ Д.М. Петров, М.И. Соловьева // Вопросы радиоэлектроники. Сер. 1. Электроника. – 1961. - №5. – С. 39-47.
11. Байбурин, В.Б.Модели и методы планируемого эксперимента: Учеб.пособие по курсу «Мат. моделирование в науч. исслед. и инж. задачах» для студентов спец. 2202, 2204 / В. Б. Байбурин, Р. П. Кутенков. – Саратов:СГТУ, 1994. -  49 с.
12Иоссель, Ю. Расчет электрической емкости: 2-е изд., перераб. и дополн/ Ю. Иоссель, Э.С. Кочанов, М.Г. Струнский. - Л: Энергоиздат, Ленингр. отд., 1981.- 228 с.
13.Хаби, В.С.  Измерение характеристического сопротивления резо­натора с бессеточным зазором[Текст]/В.С. Хаби // Электронная техника.  Сер.1. Электроника СВЧ.- 1971.- Вып. 3.- С. 138 – 140.
14. Прокофьев, Б.В.К расчету характеристического сопротивления резонаторов многолучевых вакуумных приборов СВЧ[Электронный ресурс]  / Б.В. Прокофьев,  А.В. Коннов,  В.Л. Саввин // Журнал радиоэлектроники. –2011. - №12.Режим доступа: http://jre.cplire.ru/jre/dec11/1/text.html (доступ свободный) – Загл. с экрана. – Яз.рус.