Расчет конструкции, состоящей из блоков с шестиугольной пластиной и круговой цилиндрической оболочки с окантовкой
Аннотация
Дата поступления статьи: 18.09.2013Статья посвящена прочностным расчетам составных конструкций. Рассмотрено напряженно-деформированное состояние конструкции из блоков, состоящих из основания в форме шестиугольной пластины, жестко связанной с основанием круговой цилиндрической оболочки.
Ключевые слова: пластина, оболочка, прочность, составная конструкция.
Рассмотрим совокупность отдельных блоков составной конструкции, каждый из которых представляет собой шестиугольную пластину и круговую цилиндрическую оболочку с окантовкой [1]-[10].
Для всех блоков матричное уравнение, которое связывает перемещение в вершинах пластин
( 
– номер нагружения пары соответствующих вершин; 
– номер блока;
– номер координатной оси) в собственной системе координат каждого блока с перемещениями в этих же вершинах
( 
– номера всех вершин конструкции) только в общей системе координат, имеет вид:
, (1)
где 
– матрица, которая связывает перемещения собственной и общей систем координат.
Произвольное перемещение точки любого блока в общей системе координат определяется из матричного уравнения:
. (2)
Аналогично можно получить матрицу коэффициентов через перемещения вершин в общей системе координат:
или 
(3) .
Потенциальная энергия деформации П всей системы равна сумме потенциальных энергий каждого блока:
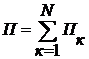. (4)
Для того, чтобы определить минимум потенциальной энергии, соответствующей действительным перемещениям, необходимо найти производные по всем перемещениям узлов:
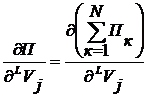, (4)
где 
– номер координатной оси, 
– номера всех вершин конструкции.
В узловых точках могут сходиться не более трех вершин (рис. 1), по одной от каждого из трех блоков.
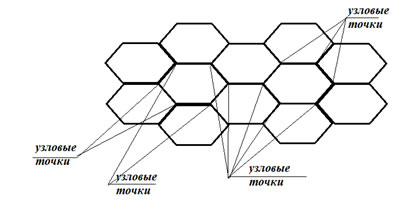
Рис. 1. – Схема составной конструкции из блоков с узловыми точками.
Для конкретного узла n потенциальную энергию можно представить в виде:
, (5)
После некоторых преобразований получим:
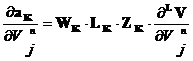и 
(6) .
Окончательно получаем
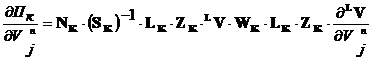. (7)
Записывая выражения (7) для всех блоков и одновременно учитывая, что соприкасающиеся друг с другом блоки по общим вершинам имеют одинаковые перемещения, получим левую часть системы линейных алгебраических уравнений относительно неизвестных перемещений узлов.
В общей конструкции имеют место три вида узлов: первый – внутренний узел (узловые точки на рис. 1), в котором сходятся три блока; второй –узел, в котором сходятся два блока; третий –узел, который примыкает только к одному блоку.
Рассмотрим нагружение всей конструкции силами, приложенными в центре каждого блока под углом ϑ (рис. 2).
Рис. 2. – Схема нагружения блока в составной конструкции.
Работа всех внешних сил определяется по формуле:
. (8)
Здесь использованы перемещения узловых точек в общей нумерации узлов. Для конкретного случая нагружения, показанного на рис.2, проекции сил равны: для узлов первого вида –
; для узлов второго вида –
.
Величина внешней работы (8) – линейная функция перемещений узловых точек. Поэтому при дифференцировании по этим перемещениям сама величина перемещения уйдет и в правых частях системы, являющейся условием минимума полной энергии деформирования конструкции остается только проекции нагрузки:
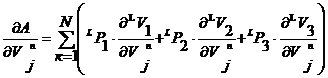. (9)
В этом выражении при дифференцировании каждый раз будет оставаться только одно слагаемое, в котором совпадает L с n , и совпадают направления координатных осей, 
– номер координатного направления.
Таким образом, правые части системы алгебраических уравнений относительно неизвестных величин перемещений узлов определены полностью. Выражения для левых частей определяются формулами:
для узла n – 
,
где 
определятся по (7).
Литература:
1. Амосов А.А. Техническая теория тонких упругих оболочек. [Текст]: Монография/ Амосов А.А. – М.:АСВ, 2009, – 332 с.
2. Филин А.П. Элементы теории оболочек.[Текст]: Монография/ Филин А.П..– Л.:Стройиздат, 1975, – 256 с.
3. Огибалов П.М., Колтунов М.Л. Оболочки и пластины.[Текст]: Монография/ Огибалов П.М., Колтунов М.Л.–М.:МГУ, 1969, – 696 с.
4. Calladine C.R. Theory of shell structures.[Text]: Monograph/ Calladine C.R. – N.Y.: Cambridge University Press, 1989, –788 p.
5. Zingoni A. Shell structures in civil and mechanical engineering.[Text]: Monograph/ Zingoni A. – N.Y.: Thomas Telford Publishing, 1997, –351 p.
6. Маяцкая И.А.,Краснобаев И.А.,Икуру Годфрей Аарон Прочностной расчет блока составной конструкции из шестиугольной пластины, круговой цилиндрической оболочки и отбортовки. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1667 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Маяцкая И.А.,Краснобаев И.А.,Икуру Годфрей Аарон Определение потенциальной энергии шестиугольной отбортовки блока составной конструкции, состоящей из основания в форме шестиугольной пластины, жестко связанной с круговой цилиндрической оболочкой. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1668 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Краснобаев И.А.,Маяцкая И.А., Икуру Годфрей Аарон Вывод соотношений сопряжения при расчете блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки[Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1669 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Краснобаев И.А.,Маяцкая И.А., Икуру Годфрей Аарон Нагружение блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1670 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. [Текст]: Монография/ Тимошенко С.П., Войновский-Кригер С. –М.:Наука, 1966, – 636 с.