Расчет деформированного состояния блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки под действием произвольной нагрузки, приложенной в его вершине
Аннотация
Дата поступления статьи: 18.09.2013Статья посвящена прочностным расчетам составных конструкций. Рассмотрено напряженно-деформированное состояние блока под действием произвольной нагрузки, приложенной в его вершине
Ключевые слова: пластина, оболочка, прочность, составная конструкция
Рассмотрим поведение блока составной конструкции под действием произвольной нагрузки (рис. 1), приложенной в его вершине [1]-[12].
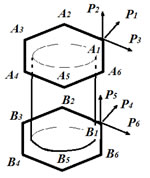
Рис. 1. – Схема нагружения тела I и тела III в к-ом блоке составной конструкции
(Р1 и Р2 – симметричное нагружение и Р3– кососимметричное нагружение узла А1; Р4и Р5 – симметричное нагружение и Р6 – кососимметричное нагружение узла В1; 
– вектор нагрузки).
В предыдущей статье рассмотрено поведение блока конструкции под действием нагружения одной вершины шестиугольной пластины А1 и соответственно точки окантовки В1 определенным образом ориентированных соответственно координатных осей.
Перемещение любой точки блока определяется по формуле:
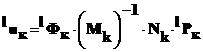. (1)
где 
– матрица аппроксимирующих функций в к-ом блоке.
Подставив в матрицу аппроксимирующих функций 
вместо произвольных координат координаты точек А1 и В1, получим перемещения этих вершин в к-ом блоке:
для точки А1–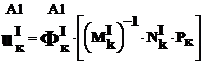
(2)
для точки В1–
(3)
Введем обозначения:
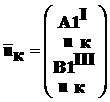– матрица-столбец перемещений точек А1 и В1;
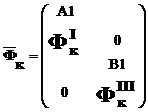– матрица аппроксимирующих функций;
; 
.
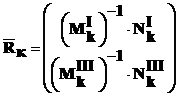Используя данные соотношения, перемещения пары вершин А1 и В1 можно представить в виде:
. (4)
Из (4) можно определить вектор нагрузок через перемещения соответствующей пары вершин:
. (5)
Подставляя (5) в (1), получим перемещения любой точки блока через перемещения соответствующей пары вершин:
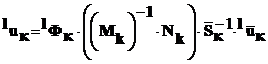(6)
или 
,
где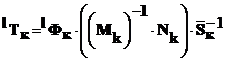 
.
Матрица коэффициентов при нагружении пары вершин тела I и тела III в к-ом блоке имеет вид:
, (7)
где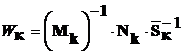 
.
Таким образом, полностью известны перемещения любой точки блока, если заданы перемещения вершин А1 и В1.
Рассмотрим положение вершин тела I и тела III (рис. 1). Для точек А1 и В1 координатный угол равен нулю, у всех остальных вершин он отличен от нуля. Значит, для нахождения перемещений от силы, действующей в вершине Ак , достаточно повернуть систему координат на угол α0 , являющийся координатным углом этой вершины (рис. 2).
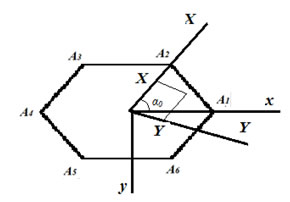
Рис. 2. – Схема для перехода от старых координатных осей к новым осям при нагружении шестиугольной пластины составной конструкции.
Переход от старых координатных осей к новым осуществляется в матрицах аппроксимирующих функций 
в соответствии с формулами:
(8)
В результате в одной и той же точке блока конструкции имеется набор перемещений, полученный приложением и снятием нагрузки, вызывающей заданные перемещения пар соответствующих друг другу вершин с первой по шестую.
Можно определить перемещения в произвольной точке блока от воздействия нагрузок во всех вершинах блока. Этому вопросу будет посвящено следующее исследование.
Литература:
1. Амосов А.А. Техническая теория тонких упругих оболочек. [Текст]: Монография/ Амосов А.А. – М.:АСВ, 2009, – 332 с.
2. Филин А.П. Элементы теории оболочек[Текст]: Монография/ Филин А.П..– Л.:Стройиздат, 1975, – 256 с.
3. Огибалов П.М., Колтунов М.Л. Оболочки и пластины[Текст]: Монография/ Огибалов П.М., Колтунов М.Л.–М.:МГУ, 1969, – 696 с.
4. Calladine C.R. Theory of shell structures.[Text]: Monograph/ Calladine C.R. – N.Y.: Cambridge University Press, 1989, –788 p.
5. Zingoni A. Shell structures in civil and mechanical engineering.[Text]: Monograph/ Zingoni A. – N.Y.: Thomas Telford Publishing, 1997, –351 p.
6. Маяцкая И.А.,Краснобаев И.А.,Икуру Годфрей Аарон Прочностной расчет блока составной конструкции из шестиугольной пластины, круговой цилиндрической оболочки и отбортовки. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1667 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Маяцкая И.А.,Краснобаев И.А.,Икуру Годфрей Аарон Определение потенциальной энергии шестиугольной отбортовки блока составной конструкции, состоящей из основания в форме шестиугольной пластины, жестко связанной с круговой цилиндрической оболочкой. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1668 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Краснобаев И.А.,Маяцкая И.А., Икуру Годфрей Аарон Энергия деформации составной конструкции, состоящей из шестиугольной пластины и круговой цилиндрической оболочки. [Электронный ресурс]// «Науковедение», 2013 №3(16). – Режим доступа: http://www.naukovedenie.ru.
/10ТРГСУ313 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Краснобаев И.А., Маяцкая И.А., Икуру Годфрей Аарон Нагружение блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки. [Электронный ресурс]// «Науковедение», 2013 №3(16). – Режим доступа: http://www.naukovedenie.ru./11ТРГСУ313 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. [Текст]: Монография/ Тимошенко С.П., Войновский-Кригер С. –М.:Наука, 1966, – 636 с.
11. Краснобаев И.А.,Маяцкая И.А., Икуру Годфрей Аарон Вывод соотношений сопряжения при расчете блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки[Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1669 (доступ свободный) – Загл. с экрана. – Яз. рус.
12. Краснобаев И.А.,Маяцкая И.А., Икуру Годфрей Аарон Нагружение блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1670 (доступ свободный) – Загл. с экрана. – Яз. рус.