О кинетике тепловыделений при затворении и твердении вяжущих
Аннотация
Знание кинетики тепловыделения дает дополнительный ключ к пониманию физико-химических процессов, связанных с твердением вяжущих. На кривых тепловыделений прослеживается три стадии. Предложены кинетические уравнения, описывающие каждую из них.
Ключевые слова: кинетика, тепловыделение, скорость, стадии, вяжущие.
Одним из косвенных методов познания сущности физических и химических процессов, протекающих при затворении водой и твердении строительных растворов, может служить исследование кинетики тепловыделения или изменения температуры смесей во времени в адиабатическом режиме проведения эксперимента. Это связано с тем, что любой динамический процесс независимо от природы его сопровождается выделением или поглощением тепла. Знание кинетических констант, таких как кон-станта скорости процесса или реакции, энергия активации, термический коэффициент, облегчает обработку экспериментальных данных и способствует объективной и более глубокой оценке влияния различных факторов на эти процессы.
Данная работа является продолжением анализа кинетических кривых тепловы-деления, рассмотренных ранее [1] и дополнительно представленных на рисунке. На кривых изменения температуры цементного теста во времени при различных условиях проведения эксперимента наблюдаются три обобщенных последовательно протекаю-щих стадии, названных так потому, что они могут включать различные по своей при-роде явления.
Стадии обусловлены: 1 — адсорбцией; П — лимитирующей скоростью химиче-ского взаимодействия; Ш — лимитирующей скоростью диффузии молекул воды через слой геля.
Первая, связанная с небольшим повышением температуры, вероятно, обуслов-лена теплотой смачивания, частичным растворением ингредиентов смеси, адсорбцией и хемосорбцией молекул дисперсионной среды — воды, как имеющей химическое средство. Учитывая малые значения теплот смачивания и растворения [2], опреде-ляющее значение будет иметь тепло, выделяющееся хемосорбцей, в результате кото-рой, возможно, образуются двухмерные фрагменты кристаллогидратов. Наличие ПАВ или других примесей может во времени растянуть этот процесс.
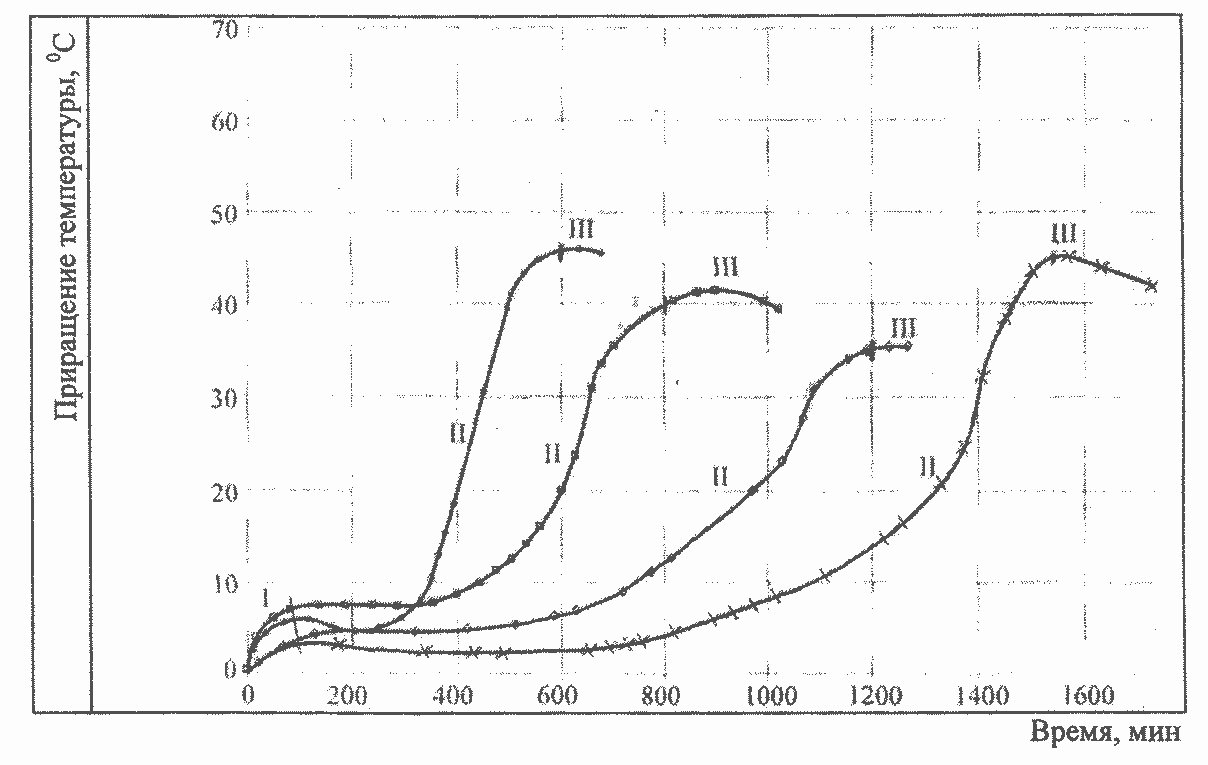 Изменение температуры цементного теста при различных условиях проведе-ния эксперимента При этом отметим, что некоторое падение температуры после первоначального повышения в начале эксперимента и более значительное в конце связано с отклонением его от адиабатного, т.е. с потерей тепла за счет теплообмена с окружающей средой.
Изменение температуры цементного теста при различных условиях проведе-ния эксперимента При этом отметим, что некоторое падение температуры после первоначального повышения в начале эксперимента и более значительное в конце связано с отклонением его от адиабатного, т.е. с потерей тепла за счет теплообмена с окружающей средой.
Вторая стадия связана с гидролизом минералов вяжущего, в результате чего из двумерных структурных элементов формируются объемные гелеобразные трехмерные
фрагменты новообразований. Этот процесс, начавшись с поверхности частиц за счет
диффузии молекул воды, через недостаточно протяженный слой геля распространяется в глубь их объема. Безусловно, химические реакции гидролиза и гидратации будут
теплоопределяющими.
Третья стадия, по-видимому, обусловлена протеканием тех же реакций, но с лимитирующей стадией диффузии молекул дисперсионной среды через слой геля, а
также процессами его кристаллизации и перекристаллизации.
Учитывая высокую водопроницаемость геля, малые значения теплот фазовых
переходов [3], тепловыделением в последней стадии можно пренебречь.
При избытке дисперсионной среды как одного из реагентов обобщенные скорости первой и второй стадий линейно зависят от площади контактов двух сред. Их можно описать кинетическим уравнением мономолекулярной реакции первого порядка [4]. Скорость процесса будет эквивалентна скорости изменения поверхности контакта и то же самое скорости изменения тепловыделения.
Рассмотрим кинетику первой стадии.
Уравнение мономолекулярной реакции первого порядка имеет вид:
dC
— = — kdτ,
С
где С — текущая концентрация реагента; k — константа скорости; τ — время.
Интегрируя его, получим 1nС = —kτ + В .
Обозначим через С0 — начальную концентрацию реагента (при τ = 0), найдем
постоянную интегрирования В = 1n С0. Отсюда С = С0е-kτ.
В нашем случае С, эквивалентно начальной интегральной поверхности раздела
фаз, или максимально возможному тепловыделению Qm, а С — эквивалентно ( Qm — Qx),
где Qx— тепло, выделившееся к данному моменту времени. Тогда Q0 — Qx = Qoe-kτ или Qx
=Qm(1 — е-kτ).
Допуская, что константа скорости адсорбции мало зависит от температуры [1],
принимая постоянной теплоемкость смеси (Суд.) и ее массу (m) можно записать
Qm = (Тm — Тo)∙Суд∙m; Qx= (Tx— Тo) ∙Cуд∙m,
где То — начальная, Tx— текущая, а Тm — максимальная температуры на первой стадии.

Из последнего выражения, используя экспериментальные зависимости темпе-
ратуры смеси от времени, легко рассчитать константу скорости процесса и оценить
влияние различных факторов на ее значение.
Для второй стадии задача осложняется тем, что константа скорости реакции
гидролиза и гидратации зависят от температуры и, согласно известному уравнению
| k=Ae- | E |
| RT |
Аррениуса, будет
где Е — энергия активации; А — постоянная величина; К— газовая постоянная.
Кинетическое уравнение для рассматриваемой стадии принимает вид
| d(Qk-Qx) | =-k(Qk-Qx), |
| dτ | |
где Qk — интегральная теплота гидролиза и гидратации; Qx— текущее выделившееся тепло.
Переходя от тепловыделения к температурам и учитывая, что k=f(Т), получим
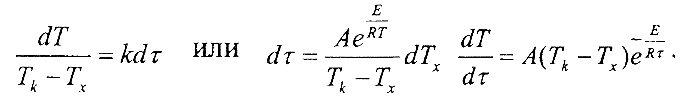
Интегрируя данное уравнение, можно получить теоретическую аналитическую зависимость между температурой смеси и временем. К сожалению, невысокие неоп-ределенные интегралы могут быть выражены через элементарные функции. В нашем случае эта зависимость примет вид
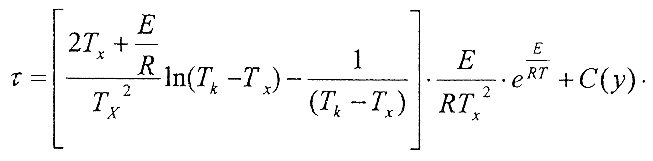
Использование ее для практических целей остается проблематичным. Задача
может найти упрощение, если функциональную зависимость Tx=f(τ) выразить исходя
из экспериментальных данных с помощью степенного ряда T= a+b∙τ +с∙τ2,
| Тогда |
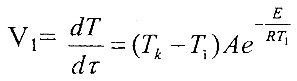 |
, где V — скорость изменения температуры смеси. |

Таким образом, используя экспериментальные данные, можно найти энергию активации, а из отношения скоростей при двух температурах можно оценить температурный коэффициент реакции (у) уравнения Вацт-Гоффа [4], т.е, определить, во сколько раз изменяется скорость реакций гидролиза и гидратации при нагревании на каждые 10 градусов.

И соответственно установить влияние различных технологических факторов на эти энергетические параметры.
Литература
1. Мальцев Н В., Мальцев В.Т. Вопросы кинетики тепловыделения в цементном тесте//Известия РГСУ. — 2007. — № 11. С. 96 — 102.
2. Эммануэль НМ., Кнорре А.Г. Курс химической кинетики. — М.: Высшая школа, 1962. — 413 с.
3. Каранетьянн МХ, Каранетьянн МЛ Основные термодинамические кон-станты неорганических и органических веществ. — М.: Химия, 1968. — 470 с. 4. Панченков ТМ., Лебедев В.Л Кинетика и химический катализ. — М.: Химия,
1985. — 589 с.