Поиск оптимального местоположения станций перегрузки твердых коммунальных отходов математическими методами
Аннотация
В статье предлагается методика оптимизации размещения мусороперегрузочных станций, позволяющая определять как местоположение, так и количество станций, что позволяет снижать как эксплуатационные так и капитальные затраты на организацию и функционирования системы обращения с отходами.
Ключевые слова: твердые муниципальные отходы, технологический процесс перевозки, критическое расстояние
В мировой практике одним из звеньев процесса повышения эффективности ликвидации твердых муниципальных отходов (далее) ТМО является внедрение технологического процесса перевозки ТМО с двухэтапным транспортированием (далее ДЭТ). Суть этого процесса заключается в использовании мусоросборных машин малой грузовместимости на первом этапе транспортирования, транспортировочных мусоровозов большой грузовместимости – на втором этапе и промежуточной перегрузки ТМО на мусороперегрузочных станциях (далее МПС).
В условиях крупных городов или больших зон функционирования системы обращения с отходами (далее СОО) поиск экономически выгодного места для создания мусороперегрузочной станции относится порой к весьма непростым задачам. Рассмотрим методику решения задачи, основанную на использовании математических и экономико-математических методов.
Вначале вводим первичные исходные данные, характеризующие размеры транспортных затрат, параметры МПС, потоки отходов и касающиеся позиций пунктов сбора и ликвидации ТМО, в том числе в перспективе.
Причем выбор пунктов сбора производится при условии экономической целесообразности вывоза из них по двухэтапной схеме. Если сбор и вывоз ТМО из пункта по такой схеме невыгоден, то его параметры исключаются из набора информации, и вывоз ТМО из него должен выполняться по прямой схеме: пункт сбора – пункт ликвидации. При этом планирование перевозок ТМО осуществляется при помощи решения транспортной задачи линейного программирования с учетом стоимости ликвидации ТМО.
Отбор пунктов сбора, подходящих для включения в двухэтапную схему, производится путем ВЕР (break-even point) – анализа нахождения критического расстояния (Lкр) и сравнения с ним расстояний от пунктов сбора до пунктов ликвидации ТМО. Если расстояние от пункта сбора до пункта ликвидации строго больше чем Lкр, то параметры пункта сбора включаются в набор данных, если не более чем Lкр, то параметры пункта не включаются в набор и перевозка осуществляется по прямой схеме.
Расчет Lкр осуществляется по формуле (1) [1]:
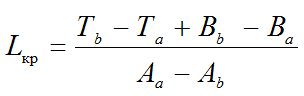 ; (1)
; (1)
где Tb, Ta – затраты на загрузку мусоровозов большой и малой вместимости соответственно, руб.; Аb, Аa – эксплуатационные затраты, зависящие от расстояния перевозки отходов, которые возникают при работе мусоровозов большой и малой вместимости соответственно, руб./км; Вb, Вa – эксплуатационные затраты, не зависящие от расстояния перевозки отходов, которые возникают при работе мусоровозов большой и малой вместимости соответственно, руб.
Основной целью формирования сети МПС является минимизация суммарных затрат на продвижение потоков ТМО от пунктов зарождения к пунктам поглощения в зоне СОО [2]. Данные суммарные затраты Cm (m – количество МПС) состоят из:
1) транспортных затрат на перемещение ТМО от пунктов сбора до МПС C(1);
2) транспортных затрат на перемещение ТМО от МПС до пунктов ликвидации C(2);
3) затрат на перевалку ТМО через МПС C(3);
4) затрат на ликвидацию ТМО C(4).
Целевой функцией формирования сети МПС в общем виде является:
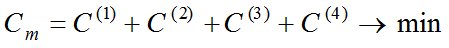 (2)
(2)
Такая задача сводится к совместному решению двух задач линейного программирования (транспортных задач): нахождения оптимального плана перевозки ТМО и одной задачи нелинейного программирования – определения координат МПС по критерию минимума суммарных затрат на продвижение потоков ТМО на выпуклой области определения переменных.
Постановка задачи. В зоне СОО имеется n пунктов сбора ТМО, объем образования ТМО в i-м пункте сбора составляет Qi м3/мес, i = 1, …, n. Имеется K пунктов ликвидации ТМО, которые могут принять не более чем 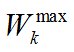 единиц ТМО, k = 1, …, K. Ограничение на пропускную способность МПС
единиц ТМО, k = 1, …, K. Ограничение на пропускную способность МПС 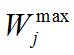 , j = 1, …, m, отсутствует. Количество пунктов перевалки ТМО (МПС) m задается. Далее везде индекс «i» используется для пунктов сбора ТМО, индекс «j» – для МПС, индекс «k» – для пунктов ликвидации ТМО. Известны:
, j = 1, …, m, отсутствует. Количество пунктов перевалки ТМО (МПС) m задается. Далее везде индекс «i» используется для пунктов сбора ТМО, индекс «j» – для МПС, индекс «k» – для пунктов ликвидации ТМО. Известны:
1) тариф на транспортирование ТМО от пункта сбора к МПС, равный Ta, руб./км;
2) тариф на транспортирование ТМО от МПС к пункту ликвидации, равный Tb, руб./км;
3) средний тариф на перевалку ТМО через МПС, равный P, руб./м3;
4) тариф на утилизацию ТМО в пункте ликвидации, равный Uk, k = 1, …, K, руб./м3;
5) средние постоянные затраты на МПС, не зависящие от объемов перевалки, равные S, руб.;
6) грузовместимость автомобиля, выполняющего перевозки от пунктов сбора ТМО до МПС, qa, м3;
7) грузовместимость автомобиля, выполняющего перевозки от МПС до пунктов ликвидации, qb, м3;
8) коэффициент уплотнения ТМО на МПС γ.
Транспортные затраты на перемещение ТМО от пунктов сбора к МПС C(1) зависят от расстояния транспортировки Lija (км) и от объема перевозок Qija (м3/мес.):
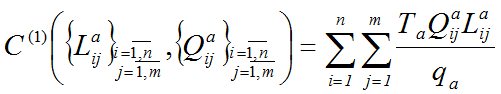 ; (3)
; (3)
где
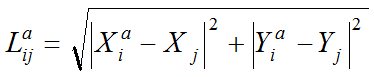 ; (4)
; (4)
Xia, Yia, Xj, Yj – координаты соответствующих пунктов, i = 1, …, n; j = 1, …, m.
Аналогично транспортные затраты на перемещение ТМО от МПС до пунктов ликвидации C(2) зависят от расстояния транспортировки Ljkb (км) и от объема перевозок Qjkb (м3/мес.):
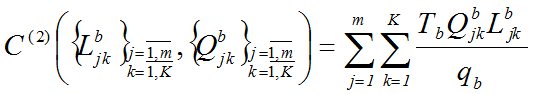 ; (5)
; (5)
где
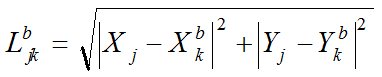 ; (6)
; (6)
Xj, Yj, Xkb, Ykb – координаты соответствующих пунктов, j = 1, …, m; k = 1, …, K.
Затраты на перевалку ТМО через МПС C(3) зависят от объема перевозок Qija (м3/мес.) и постоянных затрат S:
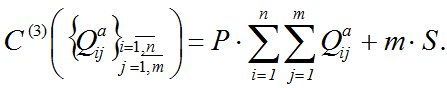 (7)
(7)
Затраты на ликвидацию ТМО C(4) зависят от объема перевозок Qjkb (м3/мес.):
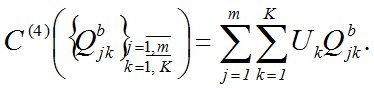 (8)
(8)
Ограничения:
– неотрицательность объемов перевозок ТМО от пунктов сбора к МПС:
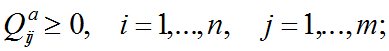 (9)
(9)
– неотрицательность объемов перевозок ТМО от МПС к пункту ликвидации:
 (10)
(10)
– полное удовлетворение потребности в сборе и вывозе ТМО из пунктов сбора:
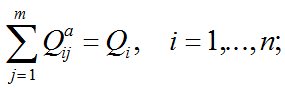 (11)
(11)
– суммарное количество ТМО, перемещаемое в пункт ликвидации, не должно превышать его максимальной мощности:
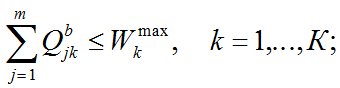 (12)
(12)
– необходимость соответствия между суммарным количеством ТМО, завезенных в пункты ликвидации, и суммарным количеством отходов, вывезенных из пунктов сбора, через достигаемое на каждой МПС уплотнение:
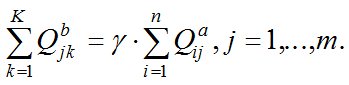 (13)
(13)
Требуется определить такие планы перевозки ТМО от пунктов сбора ТМО к МПС 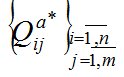 и от МПС к пунктам ликвидации ТМО
и от МПС к пунктам ликвидации ТМО  , а также координаты МПС
, а также координаты МПС 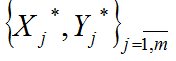 , которые бы полностью удовлетворяли потребности в перевозке ТМО, а суммарные расходы на продвижение потоков ТМО от пунктов сбора к пунктам ликвидации в зоне СОО были минимальными.
, которые бы полностью удовлетворяли потребности в перевозке ТМО, а суммарные расходы на продвижение потоков ТМО от пунктов сбора к пунктам ликвидации в зоне СОО были минимальными.
Целевая функция задачи (2) записывается в виде:
 (14)
(14)
Отметим, что задача (9)–(14) может быть решена численно для каждого значения m.
Задача поиска множества оптимальных точек размещения МПС решается при совместном определении оптимального количества и оптимального местоположения точек [3]. Критерием оптимальности такой задачи является достижение компромисса между снижением транспортных затрат и уменьшением издержек на строительство и эксплуатацию перегрузочных станций [4].
При увеличении количества перегрузочных станций в зоне СОО сокращаются транспортные затраты [5], т.е. функция транспортных затрат является монотонно убывающей, однако растут затраты на строительство и эксплуатацию МПС, т.е. функция затрат на МПС является монотонно возрастающей. При уменьшении количества МПС, наоборот транспортные затраты растут, а затраты на перегрузку МПС сокращаются. Поэтому поиск оптимальных точек размещения МПС в зоне СОО предлагается производить методом простого перебора поиска точки экстремума целевой функции (14) с ограничениями (9)–(13) при пошаговом увеличении количества МПС m = 0, 1, 2, …, до тех пор, пока целевая функция не начнет возрастать после точки минимума. Количество МПС (m), при котором целевая функция Cm достигнет минимума (Cm*), будет оптимальным (m*).
Описание алгоритма решения задачи графическим способом представлено схемой алгоритма на рис. 3.
Замечание: при m = 0 математическая модель (9)–(14) преобразуется в классическую транспортную задачу (15)–(16):
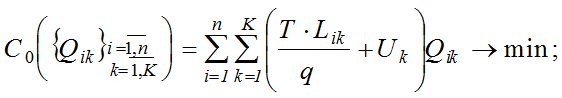 (15)
(15)
ограничения:
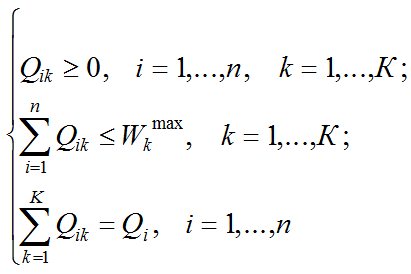 (16)
(16)
где Т – тариф на транспортирование ТМО, руб./км; q – грузовместимость автомобиля, м3.
В результате реализации алгоритма (рис. 3) определяются:
– координаты МПС 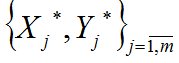 ;
;
– количество МПС m*;
– планы перевозки ТМО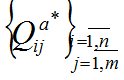 ,
, 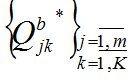 (м3/мес.);
(м3/мес.);
– значение затрат 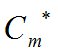 в системе ДЭТ ТМО (руб./мес.);
в системе ДЭТ ТМО (руб./мес.);
– величины пропускных способностей МПС 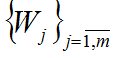 (м3/мес.), которые равняются суммарному объему перевозок в
(м3/мес.), которые равняются суммарному объему перевозок в
j-ю МПС:
(17) 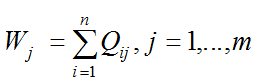 .
.
Разработанная методика оптимизации размещения МПС позволяет определять как оптимальное местоположения, так и оптимальное количество, что несомненно позволит снизить как эксплуатационные так и капитальные затраты на организацию и функционирования системы обращения с отходами.
Литература
-
Сергеева В. Г. Формирование комплексной организационно – экономической системы управления санитарной очисткой в регионе: Автореф. дис. докт. экон. наук. – С.-Петербург: 2005. – 35 с.
-
Кочерга В. Г., Поздняков М. Н. Современные подходы к разработке комплексных схем организации дорожного движения // Транспорт Российской Федерации//СПб. - №1, 2011. – с. 28-33.
-
Гайдаев В. С., Семчугова Е.Ю. Логистическая оценка доступности объектов для маломобильных групп населения / Вестник Тихоокеанского государственного университета. – № 1 (24). – 2012. – С 83-90.
-
Семчугова Е. Ю., Солонская И.Г., Гайдаев В.С Логистическое обеспечение транспортной подвижности пассажиров с ограниченными возможностями здоровья // Известия Ростовского государственного строительного университета. – №14. – Ростов н/Д: Рост. гос. стоит. ун-т, 2010. – С 75-83.
-
Кочерга В. Г., Семчугова Е. Ю., Гайдаев В. С. Логистическая система управления транспортным обеспечением маломобильных групп населения / Безопасность движения в олимпийском Сочи: Материалы Российско-Германской научно-практической конференции в рамках программы «Российско-Германский Год Науки» // Сочинский филиал МАДИ. – Сочи, 2011. – С 54-56.