Методы измерения астрономической рефракции
Аннотация
В качестве наиболее точного метода определения углов астрономической рефракции вблизи горизонта рассмотрены различные способы измерительного метода. Приведены формулы для вычисления углов астрономической рефракции азимутальным, комбинированным, интерполяционным способами, а также способом «часового угла».
Ключевые слова: Рефракция, Часовой угол, Зенитное расстояние, Широта, Склонение
25.00.34 - Аэрокосмические исследования земли, фотограмметрия
Методы измерения астрономической рефракции
Н.Н. Редичкин, И.Н. Редичкин
(Ростовский государственный строительный университет, г. Ростов-на-Дону )
Необходимость исследований астрономической рефракции обусловлена тем, что в настоящее время существенно возросли требования к точности астрономо-геодезических определений, а также появился круг научных и практических задач геодезии и астрономии, которые требуют оперативного и высокоточного определения зенитных расстояний (Z) небесных светил вблизи горизонта.
Основные пути решения этой задачи связаны с использованием возможностей современных ЭВМ и с повышением точности учета влияния внешних факторов, наиболее существенным, из которых является астрономическая рефракция (ra).
В работе [1] отмечается, что «существующая точность учета ra уже не удовлетворяет нужды традиционных разделов практической астрономии, в частности астрометрии». Кроме того, «развитие космонавтики потребовало дальнейшего повышения точности и экспрессности определений ra вблизи горизонта при выполнении расчетов траекторий искусственных и естественных космических объектов» [1].
Исследования методов повышения точности определений ra вблизи горизонта являются актуальными также, например, при выполнении работ на пунктах ФАГС (фундаментальная астрономо-геодезическая сеть), которые созданы на основании разработанной Федеральной службой геодезии и картографии России концепции и программы перехода топографо-геодезического производства на автономные методы спутниковых координатных определений.
Учет ra вблизи горизонта на основании теории рефракции (т.е. путем решения ее интеграла различными способами) не всегда соответствует предъявляемым требованиям из-за трудностей учета аномалий рефракции (Δ ra), которые вблизи горизонта могут достигать величин, превышающих точность измерений на порядок и выше. Поэтому наиболее точным является «измерительный метод» (ИМ), который представляет собой определение астрономической рефракции как разницы между измеренным зенитным расстоянием (ζ) светила и вычисленным, т.е. свободным от влияния рефракции (Z).
Исследования ИМ учета и определения углов ra и Δra являются актуальными, т.к. позволяют повысить точность измерений зенитных расстояний светил вблизи горизонта и разрабатывать способы учета аномалий рефракции на любых зенитных расстояниях.
Измерительный метод предусматривает вычисление углов ra по формуле:
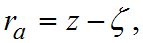 (1),
(1),
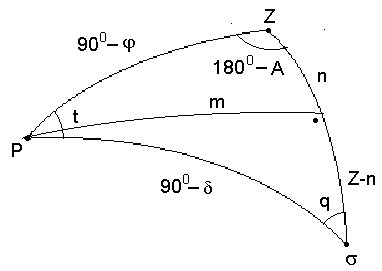
где ζ — измеренное зенитное расстояние светила; z — свободное от влияния рефракции зенитное расстояние светила, которое находят из решения параллактического треугольника PZσ (полюс-зенит-светило).
В зависимости от состава исходной информации и измеренных величин различают следующие способы определения угла ra по формуле (1) [2]:
а. Способ «часового угла»
В этом способе для определения зенитного расстояния (z=Zσ) необходимо знать широту пункта наблюдений (φ) (например, из астро-определений) и склонение (δ), которое выбирают на момент наблюдений (t) из каталога координат звезд.
Если в треугольнике PZσ измерить часовой угол (t), то по формуле (2) косинуса стороны найдем:
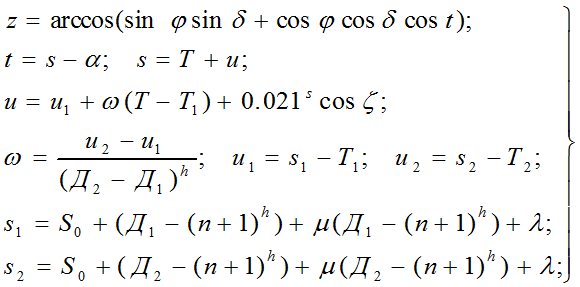 (2)
(2)
где α — прямое восхождение светила, выбираемое из каталога;
Д — местное декретное время;
s,Т,u — местное звездное время, отсчет по хронометру и поправка хронометра в момент наблюдений светила, соответственно;
Дi; ui; si; Ti — величины, полученные в моменты приема сигналов точного времени;
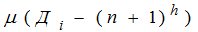 — поправка за переход от среднего времени к звездному,
— поправка за переход от среднего времени к звездному,  ;
;
n, ω— номер часового пояса места наблюдений и ход хронометра соответственно;
S0 — звездное время в 0h всемирного;
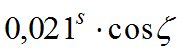 — поправка за суточную аберрацию;
— поправка за суточную аберрацию;
λ — долгота места наблюдений.
б.Азимутальный способ измерительного метода определения углов ra
В этом способе, предложенном в работе [2], необходимо иметь широту φ, склонение светила δ и его измеренный азимут А. Значения z можно вычислить по формуле (3) [2]:
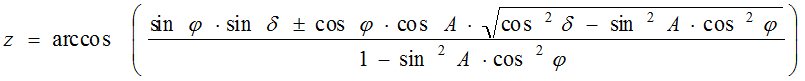 (3)
(3)
или по формуле (4), полученной на основании работы [3]:
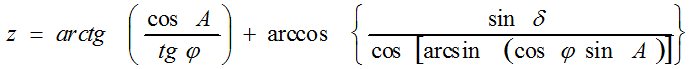 (4)
(4)
Возможность и особенности решения треугольника по (4), т.е. по двум сторонам и углу, прилежащему к одной из них, рассмотрены в работе [4].
в. Комбинированный способ
Способ определений 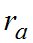 , применяя который измеряют одновременно зенитное расстояние, часовой угол и азимут небесного светила, называется комбинированным. Если экваториальные координаты наблюдаемого светила известны с высокой точностью, то для одного измеренного зенитного расстояния светила определяют два значения угла рефракции:
, применяя который измеряют одновременно зенитное расстояние, часовой угол и азимут небесного светила, называется комбинированным. Если экваториальные координаты наблюдаемого светила известны с высокой точностью, то для одного измеренного зенитного расстояния светила определяют два значения угла рефракции: 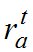 - по формулам (1), (2) и
- по формулам (1), (2) и 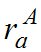 - по формулам (1), (3) или (4). Это является хорошим контролем точности наблюдений и дает возможность производить оценку точности полученных результатов.
- по формулам (1), (3) или (4). Это является хорошим контролем точности наблюдений и дает возможность производить оценку точности полученных результатов.
Поэтому в пунктах, где есть возможность решать все трудности организационного характера, связанные с регистрацией времени моментов наблюдений, применение комбинированного способа является более предпочтительным и надежным по сравнению с другими способами измерительного метода определений 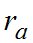 .
.
г. Интерполяционный способ определений рефракции измерительным методом
Возможность применения такого способа основана на предположении, что измерено зенитное расстояние исскуственного небесного объекта (ИНО) в момент пересечения проекций (на небесную сферу) орбиты ИНО и суточной параллели опорной звезды [5],[6].
Предполагается также, что:
- экваториальные координаты ИНО неизвестны;
- измерительным методом определены углы 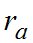 опорной звезды до и после наблюдений ИНО.
опорной звезды до и после наблюдений ИНО.
Тогда, углы  для (ИНО) можно вычислить путем нелинейного интерполирования, используя, например, интерполяционный многочлен Лагранжа и учитывая влияние параллактической рефракции.
для (ИНО) можно вычислить путем нелинейного интерполирования, используя, например, интерполяционный многочлен Лагранжа и учитывая влияние параллактической рефракции.
Из курса «Численные методы математического анализа» известно, что интерполяционный многочлен Лагранжа имеет вид [7]:
Полагая, что z=y; 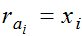 , найдем (для четырех известных
, найдем (для четырех известных 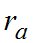 и одного неизвестного):
и одного неизвестного):
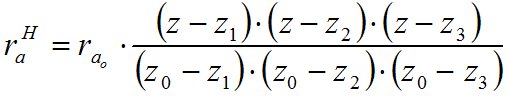 +
+ +
+
+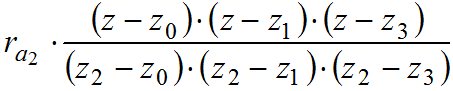 +
+ ,
,
где z - зенитное расстояние небесного объекта (ИНО), для которого определяют угол  ;
;
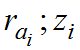 - углы рефракции и зенитные расстояния опорной звезды.
- углы рефракции и зенитные расстояния опорной звезды.
Применение этого способа возможно, если в процессе наблюдений опорной звезды удалось измерить зенитное расстояние ИНО в створе измеренных 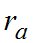 .
.
Литература
-
Алексеев А.В., Кабанов М.В., Куштин И.Ф., Нелюбин Н.Ф. Оптическая рефракция в земной атмосфере (наклонные трассы). - Новосибирск: Наука, СО АН СССР, 1983.- 230с.
-
Куштин И.Ф. Методы определения углов рефракции и поправок в дальность.- В сб.: Геодезия и фотограмметрия, изд. РИСИ, Ростов-на-Дону, 1986.- с.3-15.
-
Халхунов В.З. Курс сферической астрономии.- М.: Недра, 1972.- 304с.
-
Ганьшин В.Н., Редичкин Н.Н. Решение треугольников по двум сторонам и углу, расположенному против одной из них.- В сб.: Геодезия и фотограмметрия. Изд. РИСИ, Ростов-на-Дону, 1985.- с.45-49.
-
Куштин И.Ф. Геодезия. Учебно-практическое пособие.- М.: «Издательство ПРИОР», 2001.- 448с.
-
Редичкин Н.Н. Экспериментальные определения углов астрономической рефракции.- В сб.: Геодезия и фотограмметрия. РИСИ, Ростов-на-Дону, 1980.- с.52-65.
-
Данилина Н.И., Кваша О.П. Численные методы.- М.: Высшая школа, 1976.- 367с.