Предрасчет точности измерений астрономической рефракции вблизи горизонта
Аннотация
Разработан способ предрасчета точности измерений углов астрономической рефракции вблизи горизонта и формулы для него. Вычислены средние квадратические ошибки определения углов астрономической рефракции азимутальным способом и способом «часового угла» на полевом пункте и пункте ФАГС.
Ключевые слова: Астрономическая рефракция, Часовой угол, Зенитное расстояние, Средняя квадратическая ошибка, Предрасчет точности
25.00.34 - Аэрокосмические исследования земли, фотограмметрия
Предрасчет точности измерений астрономической рефракции вблизи горизонта
Н.Н. Редичкин, И.Н. Редичкин
(Ростовский государственный строительный университет, г. Ростов-на-Дону)
Предрасчет точности работ при определении углов астрономической рефракции (ra) и ее аномалий вблизи горизонта измерительным методом можно выполнить на основании формул (1, 2, 3, 4), известных нам из работ [1, 2]:
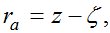(1),
где ζ — измеренное зенитное расстояние светила;
z — свободное от влияния рефракции зенитное расстояние светила, которое находят из решения параллактического треугольника PZσ (полюс-зенит-светило).
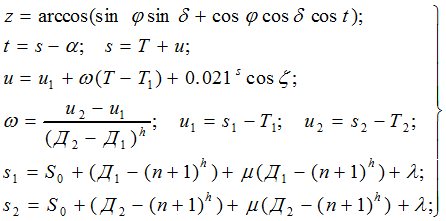(2),
где α — прямое восхождение светила, выбираемое из каталога;
Д — местное декретное время;
s,Т,u — местное звездное время, отсчет по хронометру и поправка хронометра в момент наблюдений светила, соответственно;
Дi; ui; si; Ti — величины, полученные в моменты приема сигналов точного времени;
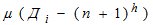— поправка за переход от среднего времени к звездному, 
;
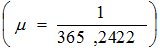n, ω— номер часового пояса места наблюдений и ход хронометра соответственно;
S0 — звездное время в 0h всемирного;
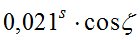— поправка за суточную аберрацию;
λ — долгота места наблюдений.
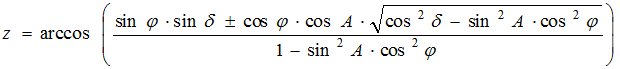(3),
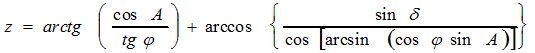(4),
где φ - широта пункта наблюдений, δ - склонение светила, А — азимут светила.
Дифференцируя формулу (1) и переходя к средним квадратическим ошибкам (СКО), найдем:
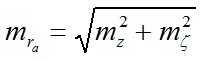, (5),
где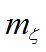 
- СКО измерений зенитных расстояний небесных светил;
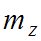- СКО вычислений (неискаженных рефракцией) зенитных расстояний небесных светил.
Выполним анализ формулы (5). Из этой формулы видно, что величина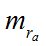 
зависит как от инструментальной точности применяемого способа измерений, так и от точности координат пунктов при вычислении z по (2, 3, 4). Точность определений координат пункта зависит от условий работ. Если работы выполняются на стационарном пункте (ФАГС), то координаты известны с высокой точностью. Если работы выполняются в произвольном пункте, в условиях кратковременной экспедиции, то неизвестные координаты места наблюдений необходимо определить в минимально короткие сроки с точностью, приемлемой для выполнения измерений ra вблизи горизонта.
Учитывая эти факторы и анализируя, например, работы [3, 4] принимаем следующие характеристики СКО, влияющих на величину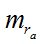 
:
- точность широты и долготы пункта характеризуется следующими СКО:
на пунктах ФАГС: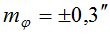 
; 
;
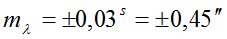на полевом (экспедиционном) пункте: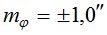 
; 
;
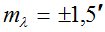- точность интерполирования экваториальных координат звезд из каталога: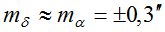 
- точность измерений часового угла и азимута составляет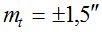 
; 
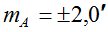, соответственно.
С учетом вышеперечисленных ошибок и полагая действие каждой из них случайным и независимым, вычислим СКО определения z – зенитного расстояния светила, неискаженного рефракцией:
- для способа «часового угла», формула (2):
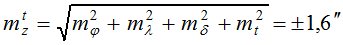- на пункте ФАГС;
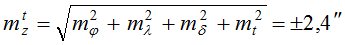- на полевом пункте;
- для азимутального способа, формулы (3, 4):
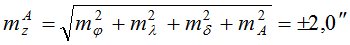- на пункте ФАГС;
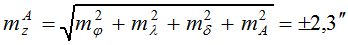- на полевом пункте.
Полученные СКО характеризуют точность определений z. Для дальнейших расчетов по формуле (5) необходимо также определить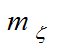 
- точность измерения зенитного расстояния светила.
На первом этапе исследований найдем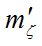 
, т.е. инструментальную СКО измерения зенитного расстояния светила.
Величину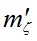 
определяют следующие СКО (применительно к теодолиту (ОТ – 02м) [5]:
- визирование на удаленную точку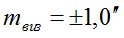 
(такая точность обусловлена формулой Нетцли) [5]:
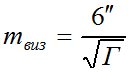, где Г =36 крат – увеличение трубы);
- определение места зенита (Мz) [5]: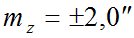 
;
- погрешность хода винтов и определения рена: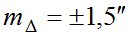 
.
Полагая влияние перечисленных погрешностей случайным и независимым, найдем:
.
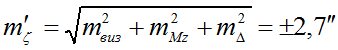Все, полученные выше, данные были использованы при выполнении расчетов по формуле (5). Результаты вычислений представлены в табл. 1.
Таблица 1
| Пункт ФАГС | Полевой пункт | ||||||||||
|
Способ «часового угла» |
Азимутальный Способ |
Способ «часового угла» |
Азимутальный Способ |
||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
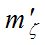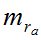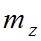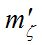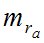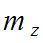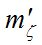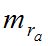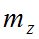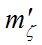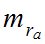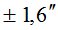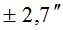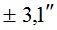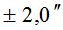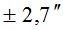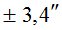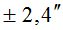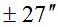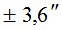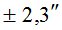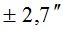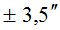Из табл. 1 видно, что точность азимутального способа измерений ra вблизи горизонта практически не зависит от того, что точность определения широты полевого пункта (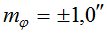
) и широты стационарного пункта (
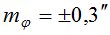) отличаются на значительную величину.
Анализ табл. 1 позволяет также сделать вывод, что способы «азимутальный» и «часового угла» практически (по точности определения ra) равнозначны, если измерения выполняют на полевом пункте.
Однако, применение способа «часового угла» дает результаты, которые для полевых условий не соответствуют точности при стационарных условиях на величину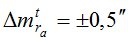 
или 14% величины 
.
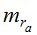Такими расхождениями можно пренебречь, если учитывать то, что на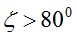 
возникают аномалии рефракции, которые могут достигать величины 
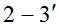и более.
Этот вывод позволяет считать, что при исследовании рефракции вблизи горизонта можно применять различные способы измерительного метода. Координаты пункта при этом достаточно знать со средней квадратической погрешностью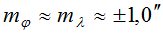 
.
В табл. 1 величина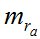 
обусловлена инструментальными погрешностями и погрешностями определения координат пункта наблюдений. Однако, на величину 
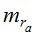существенное влияние оказывают также такие факторы, как дрожание изображения и атмосферная дисперсия.
Ошибки в положении светил из-за дрожания изображения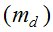 
зависят от зенитного расстояния. Их можно приближенно оценить по формуле И.Г. Колчинского 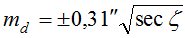[6]:
(6).
Ошибки измерений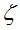 
, вызванные атмосферной дисперсией (mД) можно примерно оценить по данным, полученным в работах [6, 7], с учетом того, что «для уменьшения влияния атмосферной дисперсии инструмент диафрагмировался так, чтобы дифракционная картина получалась наиболее четкой» [7].
Значения md, вычисленные по (6) и mД, полученные в работе [7], приведены в табл. 2.
Используя для инструментальных ошибок данные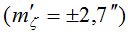 
, приведенные в табл. 1, и, считая действие 
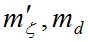и 
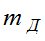случайным и независимым, получим 
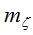- СКО измеренного зенитного расстояния светила.
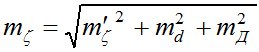. (7).
Результаты вычислений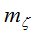 
по формуле (7) приведены в табл. 2.
Таблица 2
 |
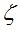800 | 850 | 880 | 890 | 89,50 | 89,80 |
 |
 |
 |
 |
 |
 |
 |
 |
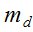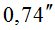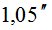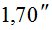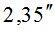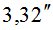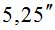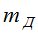1,20 | 1,30 | 1,40 | 2,0 | 2,60 | 3,50 |
 |
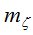3,05 | 3,18 | 3,48 | 4,11 | 5,01 | 6,86 |
По данным табл. 1 и табл. 2, выполним расчеты и найдем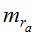 
по формуле (5). В зависимости от величины 
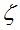получим следующие (табл. 3) значения СКО определения 
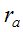измерительным методом.
Таблица 3
 |
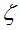800 | 850 | 880 | 890 | 89,50 | 89,80 | |
|
Пункт ФАГС |
 |
 |
 |
 |
 |
 |
 |
 |
 |
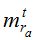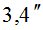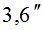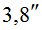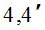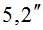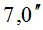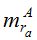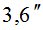3,8 | 4,0 | 4,6 | 5,4 | 7,1 | |
|
Полевой Пункт |
 |
 |
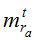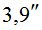4,0 | 4,2 | 4,8 | 5,6 | 7,3 |
 |
 |
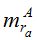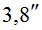3,9 | 4,2 | 4,8 | 5,5 | 7,2 | |
В таблице 3 величины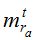 
и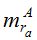 
- это СКО определения астрономической рефракции вблизи горизонта способами «часового угла» и «азимутальным», соответственно.
Из анализа табл. 3 установлено:
- способы измерительного метода определений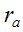 
вблизи горизонта равнозначны по точности и могут применяться для выполнения работ как на пунктах ФАГС, так и в пунктах экспедиционных, полевых работ;
- измерительный метод позволяет определять углы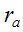 
со СКО 
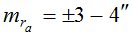на зенитных расстояниях 
;
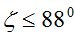- на зенитных расстояниях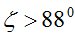 
существенное влияние оказывают дрожание изображения и дисперсия, поэтому значения 
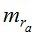достигают величины 7 и более секунд.
Литература
1. Куштин И.Ф. Методы определения углов рефракции и поправок в дальность.- В сб.: Геодезия и фотограмметрия, изд. РИСИ, Ростов-на-Дону, 1986.- с.3-15.
2. Халхунов В.З. Курс сферической астрономии.- М.: Недра, 1972.- 304с.
3. Инструкция о построении государственной геодезической сети СССР.- М.: Недра, 1966.- 341с.
4. Уралов С.С. Общая теория методов геодезической астрономии.- М.: Недра, 1973.- 271с.
5. Елисеев С.В. Геодезические инструменты и приборы.- М.: Геодезиздат, 1959.- 480с.
6. Колчинский И.Г. Два метода определения атмосферной дисперсии.- АН СССР. Астрономический журнал. Т. XXVI. №1, 1949.- с. 49-55.