Определение площади центральной проекции семейства видимых сегментов наблюдаемого объекта
Аннотация
В статье говорится об определении площади центральной проекции семейства видимых сегментов конечного множества граней наблюдаемого объекта. Предлагается центральную проекцию контролируемого объекта, попадающую на матрицу камеры, представлять в виде множества выпуклых многоугольников с целью ускорения вычисления общей площади.
Ключевые слова: сегменты многоугольников, обзора камер, алгоритм вычисления площади многоугольника
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
При проектировании объектов высокой сложности особенно трудно определить оптимальное расположение камер и взаимодействие их технических возможностей. Наиболее важный критерия в принятие решения оптимального расположения камеры наблюдения это критерий достаточной видимости охраняемой ценности. Для определения видимости контролируемого объекта необходимо определить площадь центральной проекции контролируемых граней данного объекта. Данная ненулевая площадь будет соответствовать полной видимости объекта. Такую площадь будем называть полной площадью. Другие объекты, присутствующие на плане, возможно, будут загораживать контролируемый объект. Они будут загораживать его в том случае, если они расположены между камерой наблюдения и контролируемым объектом [1, с. 39-47]. В результате видимая с камеры проекция уменьшится. Площадь видимой с камеры проекции с учетом закрывающих объектов будем называть видимой площадью.
Проекцию контролируемого объекта будем представлять в виде множества выпуклых многоугольников [2, с. 28-33]. Проекции боковых граней призмы ![]() всегда являются выпуклыми, так как выпуклы соответствующие четырёхугольники боковых граней. Проекция граней основания является выпуклой в том и только том случае, если основание призмы
всегда являются выпуклыми, так как выпуклы соответствующие четырёхугольники боковых граней. Проекция граней основания является выпуклой в том и только том случае, если основание призмы ![]() является выпуклым. Всякий невыпуклый многоугольник можно представить в виде совокупности выпуклых многоугольников при помощи нижеследующего алгоритма.
является выпуклым. Всякий невыпуклый многоугольник можно представить в виде совокупности выпуклых многоугольников при помощи нижеследующего алгоритма.
Представление невыпуклого многоугольника в виде множества непересекающихся выпуклых многоугольников
Пусть ![]() — невыпуклый многоугольник. Обозначим
— невыпуклый многоугольник. Обозначим ![]() — внутренний угол при вершине
— внутренний угол при вершине ![]() . Пусть
. Пусть ![]() и
и ![]() . В случае, если
. В случае, если ![]() , соответствующую вершину
, соответствующую вершину ![]() можно исключить из многоугольника без потери его формы.
можно исключить из многоугольника без потери его формы.
Через сторону ![]() (сторону
(сторону ![]() при
при ![]() ) построим прямую
) построим прямую ![]() (рис. 1).
(рис. 1).
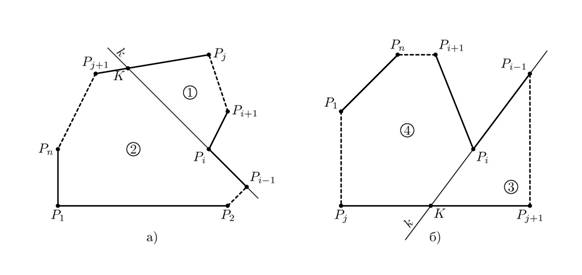
Рис. 1. Разбиение невыпуклого многоугольника на множество непересекающихся выпуклых многоугольников
Пусть ![]() — точка пересечения прямой
— точка пересечения прямой ![]() с некоторой стороной многоугольника
с некоторой стороной многоугольника ![]() (стороной
(стороной ![]() при
при ![]() ). Тогда отрезок
). Тогда отрезок ![]() разобьётисходный многоугольник на два многоугольника:
разобьётисходный многоугольник на два многоугольника:
-
при
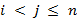 (рис. 1а):
(рис. 1а):
-
многоугольник №1:

-
многоугольник №2:
 (при
(при 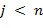 )
) -
многоугольник №2:
 (при
(при 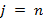 )
)
-
многоугольник №1:
-
при
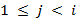 (рис. 1б):
(рис. 1б):
-
выпуклый многоугольник №3:
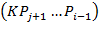
-
многоугольник №4:
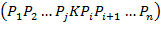
-
выпуклый многоугольник №3:
Все полученные выпуклые многоугольники добавляются в результирующее множество. Если полученный многоугольник является невыпуклым, то к нему повторно применяется данный алгоритм с добавлением результата работы алгоритма в результирующее множество.
Вычисление площади многоугольника
Для вычисления площади многоугольника ![]() , заданного координатами его вершин
, заданного координатами его вершин ![]() воспользуемся методом трапеций [3] (рис. 2):
воспользуемся методом трапеций [3] (рис. 2):
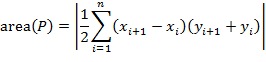
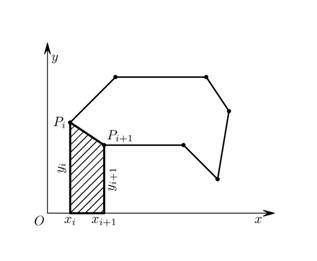
Рис. 2. Вычисление площади многоугольника
В случае, если вершины обходятся против часовой стрелки, выражение, стоящее под модулем, будет отрицательно.
Площадь множества непересекающихся многоугольников равна сумме площадей многоугольников, входящих во множество.
Определение семейства видимых сегментов множества непересекающихся выпуклых многоугольников в пространстве
Видимая часть проекции наблюдаемого объекта определяется как «разность» между проекцией контролируемых граней наблюдаемого объекта ![]() и проекцией граней других объектов
и проекцией граней других объектов ![]() , расположенных перед наблюдаемым объектом и, возможно, закрывающим его. Проекция контролируемых граней наблюдаемого объекта
, расположенных перед наблюдаемым объектом и, возможно, закрывающим его. Проекция контролируемых граней наблюдаемого объекта ![]() представлена в виде множества непересекающихся выпуклых многоугольников
представлена в виде множества непересекающихся выпуклых многоугольников ![]() . Проекция граней других объектов аналогично представлена в виде множества выпуклых многоугольников
. Проекция граней других объектов аналогично представлена в виде множества выпуклых многоугольников ![]() . Другими словами:
. Другими словами:
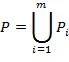
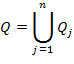
Введём определения и обозначения операций над многоугольниками и множествами выпуклых многоугольников.
Определение 1. Разбиением многоугольника ![]() будем называть множество непересекающихся выпуклых многоугольников
будем называть множество непересекающихся выпуклых многоугольников ![]() такое, что любая точка принадлежит многоугольнику
такое, что любая точка принадлежит многоугольнику ![]() тогда и только тогда, когда она принадлежит хотя бы одному многоугольнику из
тогда и только тогда, когда она принадлежит хотя бы одному многоугольнику из ![]() .
.
Точка может принадлежать нескольким многоугольникам из ![]() в том случае, если она лежит на ребре многоугольника или является его вершиной. Выпуклые многоугольники, у которых имеются только общие рёбра или вершины, но внутренние области не пересекаются, будем считать непересекающимися.
в том случае, если она лежит на ребре многоугольника или является его вершиной. Выпуклые многоугольники, у которых имеются только общие рёбра или вершины, но внутренние области не пересекаются, будем считать непересекающимися.
Определение 2. Разностью между выпуклыми многоугольниками ![]() и
и ![]() на плоскости (рис. 3) будем называть множество непересекающихся выпуклых многоугольников
на плоскости (рис. 3) будем называть множество непересекающихся выпуклых многоугольников ![]() такое, что любая точка, принадлежащая многоугольнику
такое, что любая точка, принадлежащая многоугольнику ![]() и не принадлежащая многоугольнику
и не принадлежащая многоугольнику ![]() , содержится хотя бы в одном многоугольнике из
, содержится хотя бы в одном многоугольнике из ![]() , и множество
, и множество ![]() содержит только указанные точки. Разность многоугольников на плоскости будем обозначать:
содержит только указанные точки. Разность многоугольников на плоскости будем обозначать: ![]() .
.
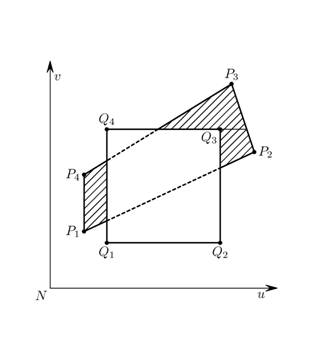
Рис. 3. Разность между выпуклыми многоугольниками на плоскости
Для проверки закрывания проекций точек граней объекта, многоугольником используется дополнительная w-координата исходной точки — аппликата. Точка, у которой аппликата больше, расположена ближе к камере наблюдения.
Определение 3. Многоугольник будет закрывать точку ![]() в том случае, если аппликата точки пересечения проецирующей прямой
в том случае, если аппликата точки пересечения проецирующей прямой ![]() с многоугольником больше аппликаты точки
с многоугольником больше аппликаты точки ![]() . В противном случае, и в случае отсутствия пересечения прямой
. В противном случае, и в случае отсутствия пересечения прямой ![]() и многоугольника, будем считать, что многоугольник не закрывает точку
и многоугольника, будем считать, что многоугольник не закрывает точку ![]() .
.
Определение 4. Будем считать, что многоугольник ![]() не закрывает многоугольник
не закрывает многоугольник ![]() , если многоугольник
, если многоугольник ![]() не закрывает ни одну точку из
не закрывает ни одну точку из ![]() .
.
Определение 5. Разностью между выпуклыми многоугольниками ![]() и
и ![]() в пространстве будем называть множество непересекающихся многоугольников
в пространстве будем называть множество непересекающихся многоугольников ![]() такое, что любая точка, принадлежащая многоугольнику
такое, что любая точка, принадлежащая многоугольнику ![]() и не закрываемая многоугольником
и не закрываемая многоугольником ![]() , содержится хотя бы в одном многоугольнике из
, содержится хотя бы в одном многоугольнике из ![]() , и множество
, и множество ![]() содержит только указанные точки. Разность многоугольников в пространстве будем обозначать:
содержит только указанные точки. Разность многоугольников в пространстве будем обозначать: ![]() .
.
Теорема 1. Если многоугольник ![]() не закрывает многоугольник
не закрывает многоугольник ![]() , то
, то ![]() .
.
Теорема 2. Если все вершины многоугольника ![]() расположены перед плоскостью, в которой лежит многоугольник
расположены перед плоскостью, в которой лежит многоугольник ![]() , то многоугольник
, то многоугольник ![]() не закрывает многоугольник
не закрывает многоугольник ![]() (рис. 4).
(рис. 4).
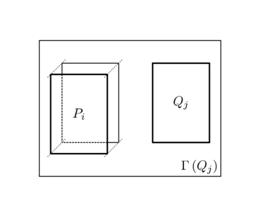
Рис. 4. Все вершины многоугольника ![]() расположены перед плоскостью
расположены перед плоскостью ![]()
Доказательство. От противного. Пусть многоугольник ![]() закрывает многоугольник
закрывает многоугольник ![]() . Тогда должна существовать, по крайней мере, одна точка
. Тогда должна существовать, по крайней мере, одна точка ![]() , расположенная за многоугольником
, расположенная за многоугольником ![]() . Пусть
. Пусть ![]() — плоскость, в которой лежит многоугольник
— плоскость, в которой лежит многоугольник ![]() . Точка
. Точка ![]() должна находиться за плоскостью
должна находиться за плоскостью![]() . Так как существует, по крайней мере, одна точка — вершина многоугольника
. Так как существует, по крайней мере, одна точка — вершина многоугольника ![]() , находящаяся перед плоскостью
, находящаяся перед плоскостью![]() , то данная плоскость пересекает
, то данная плоскость пересекает ![]() по некоторому отрезку, который разбивает многоугольник на две части: находящуюся перед
по некоторому отрезку, который разбивает многоугольник на две части: находящуюся перед ![]() и находящуюся за
и находящуюся за![]() . Часть, находящаяся за плоскостью, представляет собой многоугольник, содержащий точку
. Часть, находящаяся за плоскостью, представляет собой многоугольник, содержащий точку ![]() , вершины которого лежат на плоскости
, вершины которого лежат на плоскости![]() , а остальные являются вершинами исходного многоугольника. Таким образом, существует, по крайней мере, одна вершина многоугольника, находящаяся за плоскостью, в которой лежит многоугольник
, а остальные являются вершинами исходного многоугольника. Таким образом, существует, по крайней мере, одна вершина многоугольника, находящаяся за плоскостью, в которой лежит многоугольник ![]() , что противоречит условию теоремы. Теорема доказана.
, что противоречит условию теоремы. Теорема доказана.
Теорема 3. Если все вершины многоугольника ![]() расположены за плоскостью, в которой лежит многоугольник
расположены за плоскостью, в которой лежит многоугольник ![]() , то многоугольник
, то многоугольник ![]() не закрывает многоугольник
не закрывает многоугольник ![]() (рис. 5).
(рис. 5).
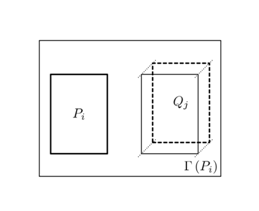
Рис. 5. Все вершины многоугольника ![]() расположены за плоскостью
расположены за плоскостью ![]()
Доказательство. Теорема доказывается аналогичным образом.
Разность многоугольников в пространстве ![]() может быть определена по следующему алгоритму.
может быть определена по следующему алгоритму.
Алгоритм 1.
-
если условие теоремы 2 выполняется, то вернуть
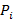 ;
; -
иначе-если условие теоремы 3 выполняется, то вернуть
 ;
; -
иначе:
-

-

-
если некоторые точки из
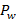 лежат перед плоскостью
лежат перед плоскостью 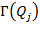 , то удалить из
, то удалить из 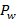 ту часть, которая лежит перед плоскостью
ту часть, которая лежит перед плоскостью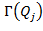 ;
; -
если некоторые точки из
 лежат за плоскостью
лежат за плоскостью 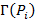 , то удалить из
, то удалить из 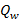 ту часть, которая лежит перед плоскостью
ту часть, которая лежит перед плоскостью  ;
; -
вернуть
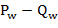 .
.
-
Определение 6. Разностью между выпуклым многоугольником ![]() и множеством непересекающихся выпуклых многоугольников
и множеством непересекающихся выпуклых многоугольников ![]() , будем называть множество непересекающихся выпуклых многоугольников
, будем называть множество непересекающихся выпуклых многоугольников ![]() такое, что любая точка, принадлежащая многоугольнику
такое, что любая точка, принадлежащая многоугольнику ![]() и не закрываемая ни одним многоугольником из
и не закрываемая ни одним многоугольником из ![]() , будет принадлежать хотя бы одному многоугольнику из
, будет принадлежать хотя бы одному многоугольнику из ![]() , и множество
, и множество ![]() будет содержать только указанные точки. Разность между многоугольником и множеством непересекающихся выпуклых многоугольников будем обозначать:
будет содержать только указанные точки. Разность между многоугольником и множеством непересекающихся выпуклых многоугольников будем обозначать: ![]() .
.
Разность между многоугольником ![]() и множеством непересекающихся выпуклых многоугольников
и множеством непересекающихся выпуклых многоугольников ![]() , может быть определена при помощи итераций вида (рис. 6):
, может быть определена при помощи итераций вида (рис. 6):
![]()
![]()

где ![]() — количество непересекающихся выпуклых многоугольников входящих во множество
— количество непересекающихся выпуклых многоугольников входящих во множество ![]() ;
; ![]() —
— ![]() -й многоугольник, входящий во множество
-й многоугольник, входящий во множество ![]() .
.
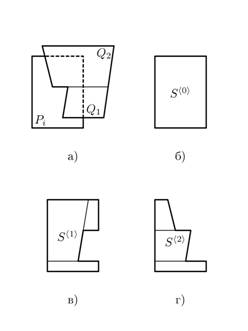
Рис. 6. Вычисление разности между выпуклым многоугольником и множеством непересекающихся выпуклых многоугольников
Определение 7. Разностью между множествами непересекающимися выпуклых многоугольников ![]() и
и ![]() будем называть множество непересекающихся выпуклых многоугольников
будем называть множество непересекающихся выпуклых многоугольников ![]() такое, что любая точка, принадлежащая многоугольнику из множества
такое, что любая точка, принадлежащая многоугольнику из множества ![]() и не закрываемая ни одним многоугольником из множества
и не закрываемая ни одним многоугольником из множества ![]() , будет принадлежать хотя бы одному многоугольнику из
, будет принадлежать хотя бы одному многоугольнику из ![]() , и множество
, и множество ![]() будет содержать только указанные точки. Разность множеств непересекающихся выпуклых многоугольников будем обозначать так же, как разность многоугольников в пространстве:
будет содержать только указанные точки. Разность множеств непересекающихся выпуклых многоугольников будем обозначать так же, как разность многоугольников в пространстве: ![]() .
.
Разность между множествами непересекающихся выпуклых многоугольников ![]() и
и ![]() может быть определена по формуле:
может быть определена по формуле:
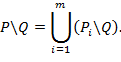
Данные преобразования позволяют определить площадь центральной проекции семейства видимых сегментов наблюдаемого объекта, в нужном виде для алгоритма проектирования расстановки камеры на объекте защиты на матрицу камеры, расположенной в выбранной точке расположения и в заданной ротации. В дальнейшем модель проецирующих объектов на камеры в возможных местах расстановки камеры и в определенном положении, ротациях, позволит рассчитать важнейшие критерии правильности выбора данного варианта расположения камер. В том числе и критерий достаточной видимости всего объекта или его важнейших составляющих. В формирование этого критерия важную роль играет знание видимой площади объекта.
Литература:
1. Белов С. В. Попов Г.А. Оценка наблюдаемости ОЗ телекамерами на основе формирования полного набора показателей эффективности их функций . Датчики и системы № 5 – М.: ООО «СепСиДат» 2009 С.39-47.
2. Попов Г.А., О систематизации методов поиска оптимальных решений. Вестник АГТУ. Сб. науч.трудов. Тел- ком- муникации, новые информ. Технологии и связь. Астрахань: 2000. С. 28-33.
3. Беляев Р. Площадь многоугольника - замкнутой ломаной без самопересечений, заданной своими вершинами в порядке обхода. [электронный ресурс] – Режим доступа. - URL: http://algolist.manual.ru/maths/geom/polygon/area.php