Оценка нахождения реконфигурируемой вычислительной системы в состояниях эффективного функционирования
Аннотация
Рассматривается методика оценки реконфигурируемой вычислительной системы в состояниях эффективного функционирования, учитывающая структуру проблемно-ориентированных вычислителей. В качестве основного математического аппарата использованы теория дискретных марковских процессов и методы теоретико-игровой оптимизации.
Ключевые слова: реконфигурируемая вычислительная система, марковские процессы, теоретико-игровая оптимизация, структура проблемно-ориентированных вычислителей
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
По состоянию на июнь 2012 года в соответствии с рейтингом и описанием 500 самых мощных общественно известных компьютерных систем мира около 80% суперЭВМ реализованы в рамках архитектуры кластерных вычислительных систем (КВС). Поскольку для обеспечения требуемой вычислительной производительности кластерная архитектура вычислительных систем подразумевает наличие в своём составе достаточно большого числа кластеров (а тем более их узлов), то одним из недостатков таких систем является относительно их невысокая надёжность [1] по показателю вероятности нахождения в состоянии, при котором они соответствуют всем требованиям нормативно-технической и (или) конструкторской (проектной) документации. Поскольку закреплённой в ГОСТ [2] основой для оценки сложных технических систем в условиях риска является аппарат дискретных марковских случайных процессов, а ряд факторов (причин неисправностей) могут не иметь вероятностного описания, то в [3] разработана методика теоретико-игровой оценки нахождения КВС в состояниях эффективного функционирования на основе марковской модели.
С другой стороны, тенденцией развития КВС является постепенный переход от их применения для решения в основном исследовательских и проектировочных задач к применению в различных системах управления реального времени. В таких системах совокупность решаемых задач требует интенсивного информационного обмена, что делает их «сильносвязанными». При этом для этого класса задач реальная производительность КВС существенно снижается и не превышает 5-10% от декларируемой пиковой производительности системы [4]. Как показано в [5] – [7], причинами этого является несоответствие архитектуры суперкомпьютера структуре решаемых задач. Для преодоления этого несоответствия в НИИ МВС ЮФУ разработана концепция создания реконфигурируемых вычислительных систем (РВС), т.е. систем с динамически перестраиваемой (перепрограммируемой) архитектурой, позволяющей создавать на её базе структуру проблемно-ориентированных вычислителей, соответствующую структуре решаемой задачи [7], [8]. Поскольку РВС, как и КВС, состоят из большого числа элементов, то задача оценки их надёжности в рамках создания отказоустойчивых вычислительных систем [9], [10] также является важной. Однако непосредственное применение известных методик, например, представленной в [3], невозможно, т.к. они не учитывают структуру проблемно-ориентированных вычислителей, реализуемых в РВС.
Таким образом, разработка методики теоретико-игровой оценки нахождения реконфигурируемой вычислительной системы в состояниях эффективного функционирования на основе марковской модели, учитывающей структуру проблемно-ориентированных вычислителей, является актуальной задачей.
Пусть РВС состоит из базовых модулей ![]() ,
, ![]() , каждый из которых включает проблемно-ориентированные вычислители
, каждый из которых включает проблемно-ориентированные вычислители ![]() ,
, ![]() ,
, ![]() (описание базовых модулей семейства РВС, состоящих из элементов, в частности, из ПЛИС, модулей памяти SDRAM, подсистемы питания, LVDS-каналов и пр., представлено в [4]).
(описание базовых модулей семейства РВС, состоящих из элементов, в частности, из ПЛИС, модулей памяти SDRAM, подсистемы питания, LVDS-каналов и пр., представлено в [4]).
В соответствие с ГОСТ [2] для описания сложной технической системы в классе марковских процессов необходимо ввести понятие состояния и перечислить все возможные состояния системы. Для этого, как и в [3], обозначим наборы двоичных чисел разрядности ![]() в виде
в виде ![]() (
(![]() ,
,![]() ), где каждый r-й разряд (
), где каждый r-й разряд (![]() ) характеризует состояние соответствующего элемента базового модуля РВС: разряд (R–1) – состояние элемента
) характеризует состояние соответствующего элемента базового модуля РВС: разряд (R–1) – состояние элемента ![]() ,…, разряд (
,…, разряд (![]() ) – состояние элемента
) – состояние элемента ![]() , разряд (
, разряд (![]() ) – состояние элемента
) – состояние элемента ![]() ,…, 0 разряд – состояние элемента
,…, 0 разряд – состояние элемента ![]() . При этом нулевое значение в разряде обозначает неисправность соответствующего элемента базового модуля РВС, а единичное – его работоспособное состояние.
. При этом нулевое значение в разряде обозначает неисправность соответствующего элемента базового модуля РВС, а единичное – его работоспособное состояние.
Однако в отличие от методики, рассмотренной в [3] для КВС, под состоянием РВС нельзя понимать совокупность состояний её любых отдельных элементов, и представить конечное множество состояний РВС выражением
![]() ,
,
поскольку такая формализация не будет отражать учёт структуры РВС.
Для такого учёта: 1) под элементами базовых модулей будем понимать их конструктивные элементы, которые при поиске и устранении неисправности базового модуля подлежат оперативной замене; 2) положим, что для решения задачи в РВС формируется V проблемно-ориентированных вычислителей – ![]() ,
, ![]() ; 3) введём в рассмотрение множества
; 3) введём в рассмотрение множества ![]() ,
, ![]() , где
, где ![]() означает принадлежность
означает принадлежность ![]() -го элемента базового модуля
-го элемента базового модуля ![]() v-му проблемно-ориентированному вычислителю.
v-му проблемно-ориентированному вычислителю.
Тогда можно определить наборы двоичных чисел разрядности V в виде ![]() ,
, ![]() ,
,![]() , где каждый
, где каждый ![]() -й разряд (
-й разряд (![]() ) характеризует состояние соответствующего проблемно-ориентированного вычислителя РВС: 0 разряд – состояние вычислителя
) характеризует состояние соответствующего проблемно-ориентированного вычислителя РВС: 0 разряд – состояние вычислителя ![]() ,…, разряд (V–1) – состояние вычислителя
,…, разряд (V–1) – состояние вычислителя ![]() . При этом нулевое значение в разряде обозначает неисправность соответствующего проблемно-ориентированного вычислителя, а единичное – его работоспособное состояние.
. При этом нулевое значение в разряде обозначает неисправность соответствующего проблемно-ориентированного вычислителя, а единичное – его работоспособное состояние.
Тогда под состоянием РВС, учитывающим структуру проблемно-ориентированных вычислителей, можно понимать совокупность их состояний, каждое из которых определяется состоянием элементов из соответствующего множества ![]() ,
, ![]() . В свою очередь, конечное множество состояний РВС определяется выражением
. В свою очередь, конечное множество состояний РВС определяется выражением
![]() , (1)
, (1)
Состояния ![]() ,
, ![]() образуют R групп с признаком принадлежности к группе
образуют R групп с признаком принадлежности к группе ![]() ,
, ![]() по общему числу единиц в двоичном числе
по общему числу единиц в двоичном числе ![]() , равном
, равном ![]() . Группы, отличающиеся по номеру на единицу, являются соседними. Множество, образованное парами соседних состояний, обозначим
. Группы, отличающиеся по номеру на единицу, являются соседними. Множество, образованное парами соседних состояний, обозначим ![]() .
.
На основе анализа функционирования РВС может быть получен граф состояний (диаграмма состояний-переходов) ![]() ,
, ![]() – множество дуг графа, с интенсивностями переходов
– множество дуг графа, с интенсивностями переходов ![]() ,
, ![]() , учитывающими действие случайных факторов.
, учитывающими действие случайных факторов.
Во множестве S можно выделить подмножество состояний ![]() , обеспечивающих эффективное функционирование РВС в системе управления реального времени с учётом отказоустойчивости, т.е. состояний, обеспечивающих удовлетворения требований к ней с заданными количественными характеристиками. В этом случае показателем эффективности РВС может являться стационарная (предельная) вероятность нахождения системы в одном из состояний из множества
, обеспечивающих эффективное функционирование РВС в системе управления реального времени с учётом отказоустойчивости, т.е. состояний, обеспечивающих удовлетворения требований к ней с заданными количественными характеристиками. В этом случае показателем эффективности РВС может являться стационарная (предельная) вероятность нахождения системы в одном из состояний из множества ![]() .
.
Тогда в условиях, определяющих возможность существования стационарных вероятностей нахождения системы в соответствующих состояниях ![]() ,
, ![]() (представленных, например, в [11]), искомая оценка может быть получена по выражению
(представленных, например, в [11]), искомая оценка может быть получена по выражению
 , (2)
, (2)
а для нахождения ![]() ,
, ![]() необходимо решение системы алгебраических уравнений вида:
необходимо решение системы алгебраических уравнений вида:
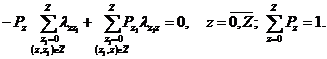 (3)
(3)
Для получения оценки стационарной вероятности нахождения РВС в одном из состояний её эффективного функционирования по выражениям (2), (3) необходимо знание интенсивностей ![]() .
.
Однако, при переходе из состояний, входящих в группу ![]() , в состояния из группы
, в состояния из группы ![]() возможны ситуации, для которых неисправность соответствующего проблемно-ориентированного вычислителя связана с несколькими причинами, определяемыми неисправностью элементов из соответствующего ему множества
возможны ситуации, для которых неисправность соответствующего проблемно-ориентированного вычислителя связана с несколькими причинами, определяемыми неисправностью элементов из соответствующего ему множества ![]() ,
, ![]() . При этом локализация неисправности (действия, направленные на идентификацию неисправной составной части или нескольких составных частей на соответствующем уровне разукрупнения [12]) однозначно влечёт и устранение этой неисправности. Например, локализация неисправности проблемно-ориентированного вычислителя осуществляется путём последовательной замены обеспечивающих его работу элементов базовых модулей (из соответствующего ему множества
. При этом локализация неисправности (действия, направленные на идентификацию неисправной составной части или нескольких составных частей на соответствующем уровне разукрупнения [12]) однозначно влечёт и устранение этой неисправности. Например, локализация неисправности проблемно-ориентированного вычислителя осуществляется путём последовательной замены обеспечивающих его работу элементов базовых модулей (из соответствующего ему множества ![]() ,
, ![]() ), рассматриваемых в качестве причин неисправности, на достоверно работоспособные. Обозначим множество пар таких состояний через
), рассматриваемых в качестве причин неисправности, на достоверно работоспособные. Обозначим множество пар таких состояний через ![]() . Тогда, если
. Тогда, если ![]() ,
, ![]() и
и ![]() , то интенсивность перехода
, то интенсивность перехода ![]() из состояния
из состояния ![]() в состояние
в состояние ![]() неизвестна, т.к. зависит от стратегии локализации-устранения неисправности и её причины. Если вероятности появления этих причин неизвестны или их оценки статистически не достоверны, то можно воспользоваться теоретико-игровым подходом, который является гарантированным в смысле достижения ситуации равновесия в антагонистической игре с матрицей выигрышей первого игрока
неизвестна, т.к. зависит от стратегии локализации-устранения неисправности и её причины. Если вероятности появления этих причин неизвестны или их оценки статистически не достоверны, то можно воспользоваться теоретико-игровым подходом, который является гарантированным в смысле достижения ситуации равновесия в антагонистической игре с матрицей выигрышей первого игрока
![]() (4)
(4)
Решение игры в чистых стратегиях (при наличии седловой точки в матрице (4)) позволяет определить искомую интенсивность в виде:
![]()
![]() . (5)
. (5)
Если равенство (5) не выполняется, то решение игры ![]() ,
, ![]() ,
, 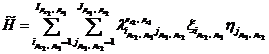 может быть получено на множествах смешанных стратегий
может быть получено на множествах смешанных стратегий ![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ) как результат решения прямой и двойственной задач линейного программирования [4].
) как результат решения прямой и двойственной задач линейного программирования [4].
При этом в качестве оценки неизвестной интенсивности ![]() принимается её математическое ожидание
принимается её математическое ожидание ![]() .
.
Тогда методика может быть представлена в виде следующей последовательности операций:
1. Формирование множества ![]() состояний РВС (1).
состояний РВС (1).
2. Оценка состояний по эффективности функционирования РВС в системе управления реального времени, учитывающая структуру проблемно-ориентированных вычислителей, и определение множества ![]() .
.
3. Формирование диаграммы состояний-переходов и определение множества ![]() пар состояний с неизвестными интенсивностями переходов.
пар состояний с неизвестными интенсивностями переходов.
4. Решение теоретико-игровых задач, определяемых матрицами (4) для всех пар индексов из множества ![]() , с получением оценок неизвестных интенсивностей переходов в виде значений интенсивностей (5) или их математических ожиданий
, с получением оценок неизвестных интенсивностей переходов в виде значений интенсивностей (5) или их математических ожиданий ![]() .
.
6. Решение системы линейных алгебраических уравнений (3) относительно предельных вероятностей нахождения системы в состояниях из множества ![]() .
.
7. Определение оценки вероятности нахождения кластерной вычислительной системы в состояниях эффективного функционирования по выражению (2).
Таким образом, разработанная методика позволяет получить гарантированную в теоретико-игровом смысле оценку нахождения реконфигурируемой вычислительной системы в состояниях эффективного функционирования в системах управления реального времени, учитывающей структуру проблемно-ориентированных вычислителей, при деградации её структуры в результате отказов отдельных элементов базовых модулей.
Кроме того, на основе полученных оценок могут быть реализованы алгоритмы оптимизации процессов поиска и устранения дефектов РВС. Для малого числа реализаций игровой ситуации применимы модели и методы решения смешанного расширения матричных игр неклассического типа, представленные в [13].
Литература:
1. Наумов А. Блейд-система T-Blade 2 // СуперКомпьютеры, 2010. – № 1. – С. 46, 47.
2. ГОСТ Р 51901.15-2005 Менеджмент риска. Применение марковских методов. – М.: Стандартинформ, 2005.
3. Строцев А.А. Методика теоретико-игровой оценки нахождения кластерной вычислительной системы в состояниях эффективного функционирования на основе марковской модели // В сб. «Суперкомпьютерные технологии (СКТ-2012) // Материалы 2-й Всероссийской научно-технической конференции. – Ростов-на-Дону: Издательство Южного федерального университета, 2012. – 410 с». – С. 192 – 196.
4. Дмитренко Н.Н., Каляев И.А., Левин И.И., Семерников Е.А. Реконфигурируемые вычислительные системы для решения вычислительно трудоёмких задач // В сб. «Труды Всероссийской научной конференции (22-27 сентября 2008 г., г. Новороссийск).- М.: Изд-во МГУ, 2008. - 468 с. ISBN 978-5-211-05616-9» . – С. 265 – 270.
5.Алдышев О.С., Дикарев Н.И., Овсянников А.П. и др. СуперЭВМ: области применения и требования к производительности // Известия ВУЗов. Электроника, 2004. – №1. – С.13–17.
6. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. –С.-Пб.: «БХВ-Петербург», 2002. –599 с.
7. Каляев И.А., Левин И.И. Модульно-наращиваемые многопроцессорные системы со структурно-процедурной организацией. – М.: Янус-К, 2003. – 380 с.
8. Каляев И.А., Левин И.И. Семерников Е.А., Шмойлов В.И. Реконфигурируемые мультиконвейерные вычислительные структуры / Под ред. И.А. Каляева. – Ростов-на-Дону: Издательство ЮНЦ РАН, 2008. – 320 с.
9. Авиженис А. Отказоустойчивость – свойство, обеспечивающее постоянную работу цифровых устройств // ТИИЭР, 1978. – Т.66. – №10. – С. 5–25.
10. Катаев О. В. Методология проектирования отказоустойчивых вычислительных систем // В сб. «Суперкомпьютерные технологии (СКТ-2012) // Материалы 2-й Всероссийской научно-технической конференции. – Ростов-на-Дону: Издательство Южного федерального университета, 2012. – 410 с». – С. 220 – 224.
11. Макаров Ю.Н., Строцев А.А. Методология исследования сложных организационно-технических систем, функционирующих в конкурентной среде при ограниченных ресурсах. Монография. Ростов-на-Дону: Изд-во ЮФУ, 2010. – 132 с.
12. ГОСТ Р 27.002-2009 (Р 53480-2009). Надёжность в технике. Основные понятия. Термины и определения. – М.: Стандартинформ, 2011.
13. Строцев А.А. Построение смешанного расширения матричной игры «неклассического» типа // Изв. РАН. Теория и системы управления. – 1998. – № 3. – С. 119–124.