Системы автоматического регулирования динамического уровня жидкости в скважине в штанговых глубинно-насосных установках

Аннотация

А.И. Исмагулова

В работе предлагается схема регулирования динамического уровня жидкости, которая может быть использована в системах нефтедобычи с целью повышения эффективности их работы. Описана схема регулятора уровня, состоящего из пропорционального и интегрального дискретных элементов, что позволило уменьшить статическую ошибку  и на основе повысить эффективность регулирования динамического уровня. Проведено моделирование процесса работы предлагаемой схемы регулирования, проанализированы результаты и выработаны рекомендации по параметрам регулятора. Описана процедура использования предлагаемой схемы также для контроля степени незаполнения насоса.

Ключевые слова: схема регулирования динамического уровня жидкости, пропорционально-интегрального регулятора уровня, регулирование динамического уровня

05.13.06 - Автоматизация и управление технологическими процессами и производствами (по отраслям)

Штанговые глубинно-насосные установки (ШГНУ) занимают важное место среди основных оборудовании, применяемых в нефтепромыслах, поскольку, несмотря на то, что в настоящее время имеются более совершенные схемы выкачки нефтепродуктов из скважины, боле половины всех скважин России эксплуатируют ШНГУ. Штанговые глубинные насосы - наиболее распространенный способ механизированной добычи нефти (порядка 60% добычи в Северной Америке и порядка 70% во всем мире). Самая частая проблема, с которой приходится иметь дело при эксплуатации этих насосов, - это их низкая производительность в результате неполного заполнения насоса жидкостью. Это происходит, если производительность и эффективность насоса превышает дебит скважины или из-за плохой сепарации газа на приеме. Производительность насоса снижается из-за попадания в него газа.
Большое влияние на эффективность процесса функционирования ШНГУ оказывают колебания уровня жидкости (нефтепродуктов), так как колебания уровня жидкости приводят к нестабильности работы насоса и, как следствие, к его быстрому износу и даже к аварийным поломкам. Поэтому задача обеспечения стабильности уровня жидкости в скважине является одной из важных задач обеспечения эффективности работы скважины. Среди работ, посвященных данной проблеме, укажем на работы [1, 2].
Одним из возможных путей решения указанной проблемы является обеспечение такого режима эксплуатации скважины, при котором уровень жидкости меняется очень медленно либо даже вообще остается неизменным. Решение указанной задачи может быть достигнуто на основе создания и внедрения систем автоматического регулирования уровня жидкости. Именно данный подход и рассматривается в данной работе. Отметим также работы [3 - 6] по данной тематике.

1. Система автоматического регулирование динамического уровня

Формирование системы автоматического регулирования динамического уровня (АРДУ)  предлагается осуществить на основе математической модели, описывающей процесс изменения уровня жидкости в скважине.
Математическую модель системы АРДУ жидкости в скважине построим на основе широко распространенного в практике нефтедобычи представления процесса перераспределения давления в скважине ( - пластового давления и Рс -давления на забое), обусловленного изменением дебита Q, дифференциальным уравнением первого порядка [7, 8]:
     (1)
параметры которого: Т_с - постоянная времени, и k_c - коэффициент продуктивности скважины, определяются геологическими характеристиками пласта и оборудованием скважины.
Дебит скважины при механизированной добыче зависит от выбора оборудования и режима работы ШГНУ, определяющих производительность насосной установки QH, следовательно, в уравнении (1) можно принять Q= QH. Далее, учитывая, что давление на забое складывается из гидростатического давления столба жидкости в стволе скважины и затрубного давления, уравнение (1) дополним уравнением связи динамического уровня с давлением:
    (2)
где - глубина спуска насоса, измеренная от устья скважины.
Структурная схема системы автоматического регулирования динамического уровня жидкости в скважине может быть представлена в виде, показанном на рисунке 1.

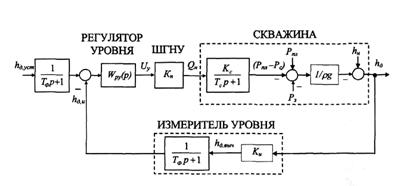
Рис. 1–Структурная схема системы автоматического регулирования динамического уровня

Приведенная схема носит общий характер, независимо от способа регулирования подачи насоса, если считать, что под управляющим воздействием на электропривод ШГНУ понимается соответствующая выбранному способу входная переменная, определяющая производительность установки.
Так, в системе управления с регулированием подачи за счет изменения числа двойных ходов путем непрерывного регулирования скорости приводного двигателя ШГНУ, управляющее воздействие имеет смысл задания скорости электродвигателя, а коэффициент передачи ШГНУ Кн характеризует зависимость подачи от скорости и определяется конструктивными параметрами насоса и ШГНУ.
В случае применения для регулирования подачи режима периодической откачки с рекомендуемыми ранее значениями периода управления , рассматриваемая система будет представлять собой систему с широтно-импульсной модуляцией управляющего воздействия определяющего относительное время работы насоса в цикле управления. В этом случае коэффициент передачи ШГНУ характеризует зависимость средней за период управления подачи насоса от управляющего воздействия.
Параметрами К_си К_ина структурной схеме рисунке 1 обозначены коэффициенты передачи скважины по дебиту и коэффициент передачи измерителя уровня, формирующего сигнал обратной связи hd.ипо расчетному динамическому уровню, полученному на основе замеров усилий в полированном штоке в соответствии с одним из описанных способов. Постоянную времени фильтра выбираем из условия обеспечения достаточной помехоустойчивости системы, учитывая, что выходной сигнал измерителя уровня косвенного действия имеет довольно высокую степень зашумления из-за влияния случайных факторов на работу скважины. Причем выбранное значение целесообразно принять в качестве некомпенсируемой постоянной времени контура регулирования, задающей его быстродействие. Опыт показал, что рекомендуемые значения с учетом запаса по производительности установки находятся в диапазоне  .
Регулятор уровня на основе разницы заданного - ,и измеренного -динамического уровня устанавливает значение необходимого времени работы двигателя в цикле управления. Расчетное значение параметра , очевидно, должно удовлетворять неравенству: , значения ограничений и в котором выбираются в зависимости от принятого способа измерения динамического уровня. При периодическом контроле, основанном на замерах усилий в позициях останова в мертвых точках, необходимо задавать , с тем, чтобы обеспечить условия для выполнения контрольного цикла измерений. При непрерывном контроле динамического уровня имеет смысл устанавливать , предусматривая возможность работы агрегата в непрерывном режиме откачки. В любом случае следует принимать , не допуская длительного простоя агрегата из-за возникающей при этом потери информации о динамическом уровне и возможности промерзания коллектора в зимнее время.
При указанных допущениях, принятых для построения структурной схемы системы автоматического регулирования динамического уровня жидкости в скважине, синтез регулятора уровня предлагается выполнять, исходя из условия обеспечения апериодического характера процесса регулирования, учитывая, что система обладает односторонней управляемостью и не может устранить перерегулирование отрицательным управляющим воздействием. В таком случае приходим к рекомендации использования пропорционально-интегрального регулятора уровня со следующей передаточной функцией:
      (3)
Регулятор незаполнения в этом случае, как регулятор внешнего контура, целесообразно выбирать интегрального типа, настраивая контур регулирования степени незаполнения насоса на модульный оптимум:
   (4)
где  - коэффициент передачи звена незаполнения.

2. Анализ процесса изменения динамического уровня жидкости в скважине

Учитывая, что рассматриваемая система является нелинейной, анализ процессов регулирования динамического уровня жидкости в скважине и степени незаполнения насоса выполним методом цифрового моделирования на основе сформированной модели.

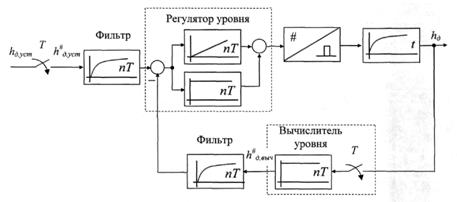
Рис. 2. –Функциональная схема цифровой модели системы автоматического регулирования динамического уровня жидкости в скважине

В данной схеме представлены следующие элементы системы: модель скважины, вычислитель динамического уровня, фильтры в каналах задания и обратной связи по динамическому уровню, регулятор динамического уровня, широтно-импульсный модулятор (ШИМ) подачи насоса. ШИМ воспроизводит режим периодической работы ШГНУ, определяя период квантования Т в системе. Период квантования Т в расчете принят в десять раз меньше постоянной времени скважины, что вполне соответствует соотношениям указанных параметров в реальных условиях. Система моделируется в относительном времени t = tp/Т, где tp - реальное время процесса. Временем вычислительного запаздывания в микропроцессорном управляющем устройстве пренебрегаем из-за его относительной малости в сравнении с периодом квантования.
В качестве модели скважины принимается линейный фильтр первого порядка, характеризующийся параметрами: Т_с - постоянная времени скважины, и К_с - коэффициент передачи скважины по расходу. Входом модели является подача насоса, выходом - динамический уровень жидкости в скважине.
В рамках предлагаемого подхода к анализу процессов регулирования вычислитель динамического уровня представлен дискретным пропорциональным звеном с квантованием по времени Г, имеющим коэффициент передачи К_и.
Регулятор уровня состоит из пропорционального и интегрального дискретных элементов, имеющих параметры: Т_р - постоянная интегратора, и К_р - коэффициент усиления регулятора.
Для моделирования предложена система основных базисных величин:
- базисное время;
- базисный уровень, соответствующий максимально возможному динамическому уровню.
Производные базисные величины: Р_б - давление, Q_б - подача и С_б -незаполнение, рассчитываются через основные величины в соответствии с вышеприведенными уравнениями (1) – (4) динамической модели объекта управления.
Учитывая достаточно большую кратность отношения постоянной времени скважины, к рекомендуемому периоду квантования с целью удобства представления результатов основные расчеты выполним, считая ШИМ усилительным звеном. В начале рассмотрим процессы регулирования с П-регулятором динамического уровня, отключив интегральную часть в его структуре. Рассмотрим расчет звеньев со следующими параметрами: Т_с = 10, К_р=10,К_с = 1, К_U=1.
Анализ показывает, что в предлагаемой системе присутствует статическая ошибка по уровню, однако процесс при соответствующей настройке регулятора не имеет перерегулирования. При увеличении коэффициента регулятора статическая ошибка уменьшается. При достаточно большом К_р (К_р>100) система переходит в автоколебательный режим на частоте модуляции ШИМ, характеризующийся чередованием крайних значений периодов включенного и отключенного состояний ШГНУ.
Применение пропорционально-интегрального регулятора уровня позволяет устранить статическую ошибку в системе.
При больших коэффициентах усиления в данном варианте построения системы также возможны субгармонические режимы.
Следует отметить, что при первом включении ШГНУ с системой автоматического регулирования динамического уровня жидкости в скважине первый проход (первый период работы станка-качалки) рекомендуется выполнять с коэффициентом модуляции 0.5, поскольку динамический уровень при этом предполагается неизвестным.
Дополнительными исследованиями подтвержден вполне очевидный характер влияния изменения параметров объекта на качество процессов регулирования динамического уровня жидкости в скважине. Так изменение коэффициента передачи скважины К_св системе с ПИ - регулятором уровня приводит к изменению соотношения времени "работа-пауза", при этом отрабатываемый уровень жидкости не изменяется. При изменении постоянной скважины Т_сдинамический уровень также не изменяется, однако изменяются его пульсации. Для их снижения, очевидно, следует уменьшать период модуляции (период коммутации ШИМ).
Изменение К_и(вследствие неверной оценки глубины) приводит к отклонению реальной глубины от заданной. Очевидно, чем больше отклонение Ки от единицы, тем значительнее реальная глубина отличается от заданной.
Таким образом, представленные результаты моделирования демонстрируют возможности достижения достаточно высокого качества регулирования уровня жидкости в скважине путем организации
периодического режима работы ШГНУ при соответствующем выборе периода модуляции и параметров регулятора уровня. При этом колебания уровня, обусловленные периодическим действием ШГНУ, остаются в приемлемых границах.
Аналогичным образом может быть построена функциональная схема цифровой модели системы автоматического регулирования степени незаполнения насоса, включающая следующие блоки: два фильтра – для входных данных и для вычислителя незаполнения,  регулятор незаполнения, САР динамического уровня ШГНУ, контроль эффекта незаполнения и вычислитель незаполнения.
Эффект незаполнения начинает проявлять себя с отметки 0,7 о.е. динамического уровня. Максимально допустимая величина незаполнения составляет 0,05 о.е. В этом варианте процессы откачки и накопления жидкости в скважине выглядят так, как показано на рисунке 3.

Рис.3. – Процессы регулирования степени незаполнения насоса

Как следует из графиков, при достижении системой уровня незаполения, заданный уровень начинает корректироваться таким образом, чтобы не допустить длительной работы с незаполнением выше допустимого. Следует отметить, что постоянную времени регулятора незаполнения желательно выбирать большую, нежели при стандартной настройке на технический оптимум. Это позволит уменьшить нежелательные колебания динамического уровня в процессе регулирования.
В случае снижения динамического уровня ниже уровня незаполнения внешний контур размыкается и система переходит в режим поддержания заданного уровня.
Таким образом, приведенная схема позволяет регулировать и поддерживать заданный уровень жидкости.

Заключение.
Разработанные функциональные и структурные схемы систем автоматического систем автоматического регулирования уровня жидкости в ШНГУ обладают достаточной общностью, позволяющей реализовать их на любой системе электропривода, как периодического действия, так и с непрерывным регулированием скорости.

Литература:
1. Буланкин Н.К. Расчет системы регулирования уровня нефти в скважине. / Сборн. научн. тр., Филиал Уфимского гос. нефт. техн. ун-та в г.Октябрьском «Актуальные проблемы нефтегазового дела» , Уфа, 2006. – с. 28-31.
2. Пугачев Е.В., Налимов Г.П., Гаус П.О. Определение уровня жидкости и скорости звука в затрубном пространстве добывающей скважины //Нефтяное хозяйство. - 2003. - № 2. - С. 64-66.
3.Силкина Т.Н., Бормашев В.П., Гаус П.О. Повышение точности определения уровня жидкости в нефтяных скважинах. / Нефтегазовые компании, 2/2005. с.12-15.
4. http://kipshop.ru/aip/index.php
5. http://teplocontrol-c.ru/katalog/7820.html
6. http://ntpo.com/patent_pumps/ patent_pump/pumps_499.shtml
7. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УрО РАН, 2000. 654 с.
8. Дорошенко В.А., Зюзев A.M., Метельков В.П. Математическое моделирование режимов работы бурового насоса II Изв. вузов. Горный журнал. 2004. №1. С. 65-70.