Системный синтез в реальном времени интеллектуально-адаптивного управления мехатронным объектом изменяемой структуры

Аннотация

Смирнов Ю.А., Гужев О.Ю.

В статье для условия устойчивости в «малом» получен алгоритм синтеза в реальном времени оптимального дискретного упреждающего управления мехатронным объектом, который совместно с алгоритмом оценки состояния дискретного фильтра Калмана реализуют электронную адаптивную систему управления. В «большом» предлагается применять управление мехатронным объектом по максимуму быстродействия с нейросетевой реализацией и интеллектуальной реализацией по «золотому правилу» лица, принимающего решение. Системный синтез предлагаемых алгоритмов в реальном времени реализует интеллектуально-адаптивную систему упреждающего управления мехатронным объектом изменяемой структуры.

Ключевые слова: мехатронный объект изменяемой структуры, критерий обобщенной работы, оценка сигналов управления, прогнозирующая модель, критерий максимума быстродействия, нейросетевая реализация по максимуму быстродействия; реализация по «золотому правилу».

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

В статье для условия устойчивости в «малом» получен алгоритм синтеза в реальном времени оптимального дискретного упреждающего управления мехатронным объектом, который совместно с алгоритмом оценки состояния дискретного фильтра Калмана реализуют электронную адаптивную систему управления. В «большом» предлагается применять управление мехатронным объектом по максимуму быстродействия с нейросетевой реализацией и интеллектуальной реализацией по «золотому правилу» лица, принимающего решение. Системный синтез предлагаемых алгоритмов в реальном времени реализует интеллектуально-адаптивную систему упреждающего управления мехатронным объектом изменяемой структуры.

Ключевые слова: мехатронный объект изменяемой структуры, критерий обобщенной работы,  оценка сигналов управления,  прогнозирующая модель, критерий максимума быстродействия, нейросетевая реализация по максимуму быстродействия; реализация по «золотому правилу».

1. Математическая формулировка задачи синтеза и метод ее решения. Рассмотрим задачу синтеза для мехатронного объекта, описываемого следующими предикатно-разностными уравнениями:

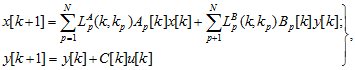               (1.1)

где 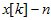-мерный вектор-столбец состояния объекта управления; 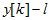-мерный век -тор-столбец положения исполнительных органов; 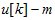-мерный вектор-столбец управ -лений; 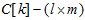– матрица переменных коэффициентов, характеризующих эффектив -ность управлений; 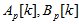– соответственно матрицы переменных коэф -фициентов состояния объекта и эффективности исполнительных органов в интервале моментов времени k между каждым 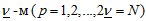структурным его изменением; – предикатные функции для матриц принимающие значе -ния 0 или 1 в зависимости от значений k и k_p, удовлетворяющие условиям единственности  и полноты                                       

  Полагаем, что в начале каждого такта работы системы блок контроля (оценивания) реального управляемого процесса определяет вектор состояния 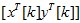и задает начальное условие в модель свободного движения мехатронного объекта  вида

                (1.2)

обеспечивая в начале каждого такта k равенство           (1.3)

Тогда получим оптимальное дискретное управление мехатронного объекта  и функцию Ляпунова-Беллмана на его решениях в виде:

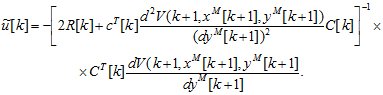                  (1.4)

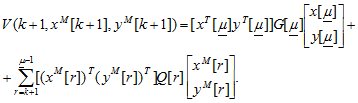            (1.5)

  2. Нейросетевой алгоритм настройки параметров прогнозирующей модели. В [5] синтез программы настройки параметров прогнозирующей модели определен в виде кусочно-линейной аппроксимации, требующий вычисления в текущий момент времени функции Ляпунова-Беллмана, ее первой и второй частной производных по вектору настраиваемых параметров . Определяя составляющие вектора настраиваемых параметров, равными значениям:

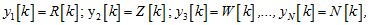
можно в качестве приближенной модели использовать нейронную сеть прямого распространения . Эта модель реализовывает отображение:

                 (2.1)

где 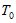 — интервал дискретности системы; — конец интервала прогнозирования.

  Нейросетевая модель представляет собой трехслойную сеть искусственных нейронов с полными последовательными связями и двумя скрытыми слоями.  Математически она модель может быть представлена в виде

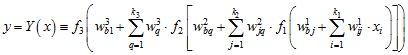.                       (2.2)

  3. Интеллектуальное управление мехатронным объектом. Электронная реализация адаптивного управления движением механическим объектом [6]  является мехатронной системой. Мехатронная функция идеальным образом моделируется в использованном методе синтеза управления  как функция Ляпунова-Беллмана. С  помощью функции Ляпунова-Беллмана, а также ее первой и второй производных  определяются адаптивные управления в «малом». В случае невыполнения условий в «малом», происходит переключение на управление по быстродействию в «большом», реализуемой нейронной сетью и относимой к искусственному интеллекту или лицом, принимающим решение.

  Рациональное соотношение искусственного и естественного интеллекта, обладающих общностью свойств по роли их в управлении,  определяется золотым сечением [7], количественной мерой которого может выступать отношение производных функции Ляпунова-Беллмана. Тогда искусственное и естественное интеллектуальное управление по правилу золотого сечения находятся соответственно в соотношении 62% и 38%. Следовательно, возможна интеллектуально-адаптивная система управления (рис. 1) на основе известной адаптивной системы управления [6].

  Целью предлагаемой системы является расширение области применения за счет автоматического сведения естественного и интеллектуально-технического нейросетевого управления в «большом» к адаптивному управлению в «малом» и наоборот.

  Цель достигается за счет введения в известную систему [6] блока 24 суммирования, блока 25 одиннадцатого ключа, блока 26 искусственного нейросетевого управления по быстродействию, блока 27 естественного автоматизированного принятия решения и управления.

ЛИТЕРАТУРА

  1. Красовский А.А., Буков В.Н., Шендрик В.С. Универсальные алгоритмы оптимального управления непрерывными процессами. – М.: Наука, 1977.

  2. Жук К.Д., Тимченко А.А. Автоматизированное проектирование логико-динамических систем. – Киев: ИК АН УССР, 1981.

  3. Смирнов Ю.А. Нейросетевое управление в мехатронике. Новые технологии, конструкции и процессы производства: Сб. научн. Тр./ Рост гос. Акад. с.-х. машиностроения. – с 132-137.

  4. Смирнов Ю.А., Тищенко Л.Г. Синтез дискретного алгоритма управления положением исполнительных органов объекта, описываемого логико-разностными уравнениями // Изв. ВУЗов. Приборостроение. 1984. № 6.

  5. Смирнов Ю.А. Синтез оптимальной программы настройки параметров прогнозирующей модели объекта изменяемой структуры. Математические методы и технологии в технике: Сб. науч. тр. / Саратовский гос. университет. Саратов, 2008.

  6. Смирнов Ю.А. Адаптивная система управления. Авторское свидетельство СССР №1464139, кл. G 05 B 13/02, 1987.

  7. Парфенов И.И. Цепные дроби — ожерелье мехатроники. — М.: КомКнига, 2007. — 120 с.