Разработка генератора псевдослучайных чисел на точках эллиптической кривой

Аннотация

М.Г. Бабенко, Н.Н. Вершкова, Н.Н. Кучеров, В.А. Кучуков

В статье рассматриваются генераторы псевдослучайных чисел, постороенные на точках эллиптической кривой над конечным полем, и алгоритмы создания неприводимых многочленов над простым полем, выделяются их основные особенности и преимущества. Авторами проводится анализ алгоритма построения генераторов псевдослучайных чисел на точках эллиптической кривой с использованием неприводимого многочлена третьей степени над конечным полем и проведением вычислений в системе остаточных классов. По результатам компьютерного моделирования показываются преимущества разработанного алгоритма в скорости работы и обеспечении критостойкости системы.

Ключевые слова: генератор псевдослучайных чисел, эллиптическая кривая, система остаточных классов, криптографическая безопасность, неприводимые многочлены

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Псевдослучайные последовательности используются для генерации секретных ключей шифрования, для вычисления цифровой подписи и для работы многих алгоритмов аутентификации. Одним из инструментов построения генераторов псевдослучайных чисел являются неприводимые многочлены над простым полем и эллиптическая кривая над конечным полем.
Поставим задачу проанализировать существующие генераторы псевдослучайных чисел на точках эллиптической кривой и построить генератор на эллиптической кривой с использование неприводимых кубических многочленов  над . Разобьем поставленную задачу на подзадачи.

1. Анализ генераторов псевдослучайных чисел, построенных на точках эллиптической кривой.
2. Анализ алгоритмов построения неприводимых многочленов  над  и исследование свойств его корней.
3. Алгоритм генерации псевдослучайных чисел на точках эллиптической кривой с использованием неприводимого многочлена 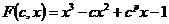 над .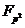

Анализ генераторов псевдослучайных чисел, построенных на точках эллиптической кривой
Генератор псевдослучайных последовательностей должен удовлетворять следующим двум требованиям, предложенным в работе[1]:

1. Статистической безопасности: последовательность, созданная генератором псевдослучайных чисел, должна статистически ничем не отличаться от абсолютно случайной последовательности.
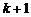2. Криптографической безопасности: зная -битов последовательности, возможно предсказать следующий или-бит.

Эллиптическая кривая широко используется для построения криптосистем [2]. Одним из инструментов построения генераторов псевдослучайных последовательностей является эллиптическая кривая над конечным полем.
Эллиптическая кривая  над простым полем , где , задается уравнением в форме Вейерштрасса , где .
В работе [3] Hallgren S. предложил построение  генераторов псевдослучайных чисел, которое называется арифметической прогрессией на  с начальным членом , разностью  и которое задается следующим рекуррентным соотношением:
, ,       (1)
где символом  обозначена групповая операция в .
Выходными значениями генератора (1) являются либо точки ,  либо только их абсциссы , либо только их ординаты .
Следует также отметить статистическую безопасность генератора псевдослучайных чисел, построенного на базе арифметической прогрессии на эллиптической кривой. Она обладает хорошими статистическими свойствами [4], а именно равномерностью распределения элементов арифметической прогрессии для большого . Порядок величины отклонения от равномерности равен .
Криптографическая безопасность арифметической прогрессии была исследована Gutierrez J. и Ibeas A. в работе [5]. В ней описан эффективный алгоритм нахождения  для генераторов, построенных на базе арифметической прогрессий на эллиптической кривой,если известна разность  и старшие биты  и . Однако при таком подходе алгоритм не обладает криптографической безопасностью.
Анализ алгоритмов построения неприводимых многочленов  над  и исследование свойств его корней
Для построения псевдослучайных чисел воспользуемся неприводимым многочленом третьей степени  над . Корни  многочлена  обладают следующими замечательными свойствами:
1.
2.  –образующий элемент подгруппы  порядка  
Для построения генератора псевдослучайных чисел нужно уметь находить неприводимые многочлены , причем вероятность того, что  окажется неприводимым многочленом при случайном выборе  из , равна . В работах [6-8] приведено несколько алгоритмических тестов  на неприводимость. Самый быстрый алгоритм работает за  умножений в  [8], но при использовании  размером в  бит для вычисления потребуется  умножений с числами длиной в  бит, что приводит к большим временным затратам и затрудняет использование этого алгоритма. В работе [9] нами был предложен эффективный способ построения неприводимых многочленов  над , основанный на нахождении  -неприводимого многочлена в , где - квадратичный невычет в , и следующей теореме.
Теорема 1. Пусть  - квадратичный невычет по модулю  и  - неприводимый многочлен в . Тогда , где  и , неприводим в .
Алгоритм генерации псевдослучайных чисел на точках эллиптической кривой с использованием неприводимого многочлена  над
Так как корень  неприводимого многочлена третьей степени  над  обладает свойством   и является порождающим элементом подгруппы в  порядка , то его элементы можно представить в виде , где  и .
Выберем шесть точек на эллиптической кривой . Тогда последовательность будет генерироваться по следующей формуле: .
Выходными значениями генератора  являются либо точки ,  либо только их абсциссы , либо только их ординаты .
Для обеспечения криптографической безопасности эллиптическая кривая должна удовлетворять следующим требованиям международного стандарта ISO/IEC CD 15946-2:
1.
2. , где  – простое число,
3. .
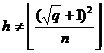4. должно выполняться MOV условие с целью исключения криптографически слабых кривых , , .
Условие 4 позволяет добиться того, что нельзя эффективно применить метод дискретного логарифмирования из работы [10], а условие 2 обеспечивает неприменимость  методом спуска Вейля [11] к взлому криптосистемы.
Результат компьютерного моделирования разработанной последовательности псевдослучайных чисел над полями размерностью 521 бит приведен в таблице 1.
Таблица № 1
Сравнительная оценка временных показателей генераторов псевдослучайных чисел при использовании различных систем счисления. (Время в миллисекундах)

Заключение
1. Анализируя полученные результаты, можно сделать вывод о том, что преимущество в скорости для алгоритма псевдослучайных чисел, построенного с использованием эллиптической кривой и неприводимого многочлена третьей степени  над , вычисления в которой производятся в системе остаточных  классов с использованием методов из работы [12], составляет 133% относительно метода, где вычисления производятся в позиционной системе счисления.
2. Работа выполнена при поддержке гранта ФЦП 14.В37.21.1128

Литература

1. Рябко Б. Я., Фионов А. Н. Криптографические методы защиты информации: Учебное пособие для вузов. – М.: Горячая линия–Телеком, 2005. – 229 с.
2. Koblitz N. Elliptic curve cryptosystems // Mathematics of Computation, 1987. Vol. 48. No. 177, P. 203-209.
3. Hallgren S. Linear congruential generators over elliptic curve. // Cornegie Mellon Univ., 1994, CS-94-M3, P. 1-10.
4. Nahassni E.E., Shparlinski I. On the uniformity of distribution of congruential generators over elliptic curves. // In: Sequences and their applications. – London: Springer, 2002, P. 257-261.
5. Gutierrez J., Ibeas A. Inferring sequences produced by a linear congruential generator on elliptic curves missing high-order bits // Designs, Codes and Cryptography, 41, 2007, P. 199-212.
6. Lenstra A.K., Verheul E.R. The XTR public key system // Proceedings of Crypto 2000, LNCS 1880, Springer-Verlag, 2000  – pp. 1-19
7. Lenstra A.K., Verheul E.R. Key improvements to XTR // Proceedings of Asiacrypt 2000, LNCS 1976, Springer-Verlag, 2000 – pp. 220-233
8. Lenstra A.K., Verheul E.R. Fast irreducibility and subgroup membership testing in XTR // Proceedings of PKC 2001, LNCS 1992,l Springer-Verlag, 2001 – pp. 73-86
9. Бабенко М.Г., Бабенко Н.А.О выборе неприводимых многочленов для криптосистемы XTR. Проблемы математики и радиофизики в области информационной безопасности: I Всероссийская конференция, г. Ставрополь, 17-19 октября 2012 г. Северо-Кавказский федеральный университет. – Ставрополь: Издательско-информационный центр «Фабула», 2012. – С.
10. Menezes A., Okamoto T., Vanstone S., Reducing elliptic curve logarithms to logarithms in a finite field // IEEE Transactions on Information Theory 39 – 1993. P. 1639-1660
11. Gordon M. D. A Survey of Fast Exponentiation Methods // Journal of Algorithms 27. – 1998. P. 129-146..
12. Червяков Н. И. Методы, алгоритмы и техническая реализация основных проблемных операций, выполняемых в системе остаточных классов // Инфокоммуникационные технологии. – №4, 2011. – С. 4-12.