Технология решения задач формирования эффективных сбалансированных малых групп в среде MS Excel

Аннотация

Н.Ф. Новосельская, Т.А. Ходарева

Предлагается методика формирования малых рабочих групп ― экспертов, команд проекта  ―  на основе модели отношений в группе в виде знакового неориентированного графа. Формирование сбалансированной группы сводится к задаче линейного программирования, которая решается в среде MS Excel путем итеративного использования надстройки Поиск решения и модуля VBA до тех пор, пока не будет сформирована оптимальная группа, соответствующая требованиям математической модели баланса.
Ключевые слова: знаковые графы, модели, малая группа, критерии сбалансированности, алгоритм формирования, уровень  компетентности, линейное программирование, MSexcel, язык VBA, оптимальная сбалансированная группа.

08.00.05 - Экономика и управление народным хозяйством (по отраслям и сферам деятельности)

Малой группой считается коллектив лиц, принимающих решения: комиссия экспертов, участники рабочих групп проекта, группы национальностей и т.п.
Малая группа «сбалансирована», если она обладает способностью хорошо работать совместно и эффективно выполнять поставленные перед ней задачи.
Подходящей моделью для представления отношений между людьми в малых группах (например, отношений «индивид А знаком с индивидом В», «лицо А доверяет лицу В» и т.п.) являются знаковые графы (орграфы). При построении модели люди представляются вершинами графа, а ребра (дуги) графа интерпретируются как некоторые отношения. Если между двумя лицами А и В имеются сильные отношения «симпатии-антипатии» либо желания «соглашаться-не соглашаться», ребру (дуге) {А, В} приписывается знак плюс (или минус).
В случае симметричных отношений ситуация представляется неориентированным знаковым графом, вершины которого соответствуют субъектам отношений. Петли в знаковом графе исключены, так как случай отношения симпатии или антипатии к самому себе не рассматривается.
При построении модели малой рабочей группы можно предполагать симметричность отношений в силу следующих предпосылок:
- если одно лицо имеет сильную антипатию к другому, то в рабочей обстановке этот факт вызовет у второго лица отрицательные эмоции, что не будет оказывать положительное влияние на ход всей работы,
- если одно лицо имеет симпатию ко второму и у второго нет антипатии к первому, то этот факт будет иметь положительное влияние на качество их совместной работы.
Изучение малых групп из различных сфер человеческой деятельности позволило исследователям Картрайту и Харари сформулировать математическую модель сбалансированности [1]: малая группа может считаться сбалансированной, если она представляется сбалансированным знаковым графом.
Критерий сбалансированности любого знакового графа дает теорема Харари[2] – теорема о балансе, в соответствии с которой множество всех вершин графа можно разбить на два подмножества так, чтобы каждое положительное ребро из множества всех вершин соединяло вершины одного подмножества и каждое отрицательное ребро из множества всех вершин соединяло вершины разных подмножеств.
Неориентированный знаковый граф является сбалансированным, если все его циклы положительны.
Таким образом, малая группа будет сбалансированной, если каждый цикл в ее знаковом графе положителен.
Рассмотрим технологию формирования сбалансированных рабочих групп на примере решения следующей задачи:
составить из имеющихся 10 кандидатов максимально компетентную и работоспособную (сбалансированную) группу экспертов с учетом ограничения по стоимости их совместной работы в проекте (в соответствии с финансовым планом) и некоторых дополнительных ограничений. В качестве дополнительных условий можно рассмотреть следующие:

1. лимит финансирования экспертной группы ограничен 450 тыс. руб.,
2. эксперт Э₆ может быть привлечен к работе только в том случае, если будет привлечен эксперт Э₁ (в силу специализации экспертов и методов их работы),
3. эксперты Э₅, Э₇ и Э₉ являются представителями некоторой компетентной организации, и присутствие хотя бы одного из них в экспертной группе обязательно,
4.  эксперты Э₁ и Э₅ по субъективным причинам отказываются работать вместе.

Алгоритм формирования сбалансированной группы экспертов включает следующие этапы:

1. разработка методики оценки уровня компетентности кандидатов,
2. вычисление коэффициентов компетентности кандидатов,
3. проведение опроса кандидатов в эксперты по критерию их готовности к совместной работе и представление результатов опроса в виде знакового графа, в котором его ребра в случае симпатии (антипатии) к другим кандидатам обозначаются соответственно знаками «плюс» (+) или «минус» (-). В качестве составляющих критерия готовности можно рассматривать такие личностные качества, как лояльность, инициативность, готовность помочь, терпимость, чувство симпатии (антипатии) и т.п.,
4. формирование математической модели задачи;
5. решение задачи в MS Excel и анализ полученных результатов.

На этапе 1 для определения уровня компетентности кандидата в экспертную группу по аналогии с методикой [3, с. 30-32] предлагается оценивать его компетентность величина k, которая вычисляется на основе суждения эксперта о степени своей информированности k_c по решаемой проблеме и его оценки другими экспертами k_об с помощью формулы:
k=k_c + k_об.
Показатель самооценки kc получается по десятибалльной шкале, приведенной в таблице 1. Диапазон изменения этого коэффициента от 8 до 45 баллов включительно.
В таблице 2 приведены балльные оценки общего критерия оценки компетентности k_об.
Таблица 1. Балльная шкала оценок значения показателя k_c

Диапазон изменения критерия k_об - от 6 до 50 баллов включительно. Следовательно, балльная оценка компетентности каждого кандидата k может изменяться в диапазоне от 14 до 95 баллов включительно.

Таблица 2. Балльная шкала оценок коэффициента k_об

Диапазон изменения критерия k_об - от 6 до 50 баллов включительно. Следовательно, балльная оценка компетентности каждого кандидата k может изменяться в диапазоне от 14 до 95 баллов включительно.
В таблице 3 приведены результаты 2-го и 3-го этапов. Данные таблицы 3 симметричны относительно главной диагонали в силу симметричности отношений между субъектами малой группы.
Модель отношений в группе, представленных в таблице 3. описывается знаковым неориентированным графом (рисунок 1), где симпатии в отношениях между двумя лицами (знак +) показаны ребрами темного цвета, а антипатии (знак -)  – ребрами светлого цвета.

Таблица 3. Данные о кандидатах в экспертную группу

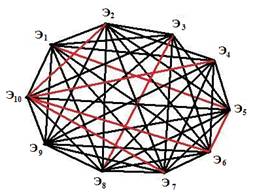
Рисунок 1 – Знаковый граф

На этапе 4 – этапе построения математической модели задачи, – в первую очередь, необходимо определить ее класс.
Решаемую задачу можно отнести к задачам линейного программирования (ЗЛП), если в качестве целевой функции выбрать показатель максимальной суммарной компетентности для всей группы. Тогда математическая постановка сводится к формированию целевой функции и ограничений оптимизационной модели задачи.
Искомыми результатами решения задачи являются хi, где i=1,2,3,...,10, - факт включения либо невключения i-ого кандидата в экспертную группу, которые могут принимать одно из двух целочисленных значений: 1 - включение в группу, 0 - невключение в группу.
Тогда целевая функция (суммарная оценка компетентности группы) будет иметь вид:

,
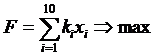где k_i – балльная оценка компетентности i – ого кандидата,
x_i – факт включения i – ого кандидата в экспертную группу.

Ограничения задачи составляют следующие условия:

• ограничение на целочисленность и на значения искомого результата:

х, - целое и

• ограничение финансирования, равное суммарному гонорару членов экспертной группы, которое не должно превышать выделенного лимита в 450 тыс. руб.:

, где    g_i– размер гонорара i – ого кандидата в экспертную группу;

• дополнительное условие о привлечении эксперта Э₆ к работе:

х_Э1=х_Э6,
т.е. если включен в группу эксперт Э₁, то включен и эксперт Э₆, если не включен в группу эксперт Э₁, то не включен и Э₆;

• дополнительное условие об экспертах Э₁ и Э₅:

х_Э1 + х_Э5 <= 1,
т.е. в экспертную группу могут быть включены либо эксперт Э₁, либо эксперт Э₅, либо ни один из них;

• дополнительное условие о включении в экспертную группу экспертов Э₅, Э₇ и Э₉:

х_Э5+ х_Э7 + х_Э9 >= 1,
т.е. в экспертную группу должен быть включен хотя бы один из экспертов Э₅, Э₇ и Э₉.
Последний 5 этап – этап решения задачи в MS Excel с помощью инструмента Поиск решения и анализ полученных результатов.
На рисунке 2 представлена электронная форма Excel для ввода математической модели задачи.

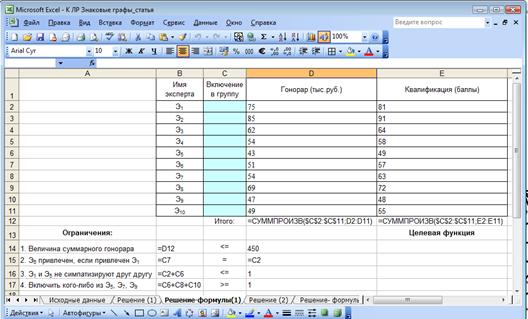
Рисунок 2 – Форма в Excel для ввода исходных данных и математической модели задачи.

Процесс решения является итерационным: на каждой итерации анализируется математическая модель баланса полученной группы экспертов, и, если условие баланса не выполняется, в математическую модель задачи вводятся новые дополнительные ограничения для исключения тех отношений между членами группы, которые нарушают сбалансированность представляющего ее знакового графа. Смысл новых ограничений состоит в том, что все вершины (кандидаты), вошедшие в отрицательные циклы, не могут быть включены в экспертную группу одновременно.
Например, если отрицательному циклу принадлежат вершины Э₇, Э₁₀ и Э₁, то какого-либо из этих кандидатов целесообразно вывести из группы. Для этого в постановку задачи вводится дополнительное условие:
х_Э7 + х _Э10 + х _Э1 <= 2,
Для облегчения обработки данных таблиц, описывающих знаковый граф очередной сформированной группы, на Visual Basic for Аррlications был реализован алгоритм перебора, позволяющий в автоматическом режиме находить список вершин (кандидатов), принадлежащих отрицательным циклам.
Итерационный процесс продолжается до тех пор, пока не будет найдена оптимальная сбалансированная группа.
Заметим, что при формировании экспертной группы мы ставили целью создание высококвалифицированной группы, расходы на которую не превышают заданного лимита денежных средств.
Если высокая квалификация создаваемой группы не имеет решающего значения, и преобладает стремление максимально сэкономить денежные средства, то в качестве целевой функции можно взять минимизацию гонорара формируемой группы,  а на уровень требуемой квалификации группы наложить нижнее ограничение: суммарная квалификация не должна быть меньше указанной величины.

Список источников:

1.  Cartwright D. and Harary F. Structural Balance: A Generalization of Heider's Theory. - Psych. Rev., 63, 1956, p. 277-293.
2.  Лихтенштейн В.Е. Информационные технологии в бизнесе. Практикум: применение системы Decision в решении прикладных экономических задач: уч. пособие. – М.: Финансы и статистика, 2009.
3. Евланов Л.Г., Кутузов В.А.  Экспертные оценки в управлении. – М.: Экономика, 1978.