Гидростатические параметры новых пьезоактивных 2–2–0-композитов на основе кристаллов 0,67pb(mg_1/3nb_2/3)o₃ – 0,33pbtio₃

Аннотация

С.В. Глушанин

Предложена схема усреднения электромеханических свойств 2–2–0-композитов на основе моно- и полидоменных кристаллов PMN–0,33PT. Рассчитаны и проанализированы концентрационные и ориентационные зависимости гидростатического пьезокоэффициента d*h и гидростатического коэффициента электромеханической связи k*h  2–2–0-композитов «кристалл – пористый полимер», а также показаны преимущества данных композитов по сравнению с ранее исследованными.
Ключевые слова: композит, пьезоэффект, пьезоэлектрик, связность, кристалл, микрогеометрия, твердый раствор, сегнетоэлектрик

01.04.07 - Физика конденсированного состояния

Предложена схема усреднения электромеханических свойств 2–2–0-композитов на основе моно- и полидоменных кристаллов PMN–0,33PT. Рассчитаны и проанализированы концентрационные и ориентационные зависимости гидростатического пьезокоэффициента  и гидростатического коэффициента электромеханической связи  2–2–0-композитов «кристалл – пористый полимер», а также показаны преимущества данных композитов по сравнению с ранее исследованными.
Кристаллы твердых растворов релаксоров-сегнетоэлектриков (1 – х)Pb(Mg_1/3Nb_2/3)O₃–xPbTiO₃ (PMN–xPT) при молярных концентрациях х вблизи морфотропной границы находят всё большее применение в качестве пьезоактивных компонентов современных композиционных материалов (композитов, см., например, [1–3]). Эти материалы используются в качестве активных элементов сенсоров, актюаторов, гидрофонов и других пьезотехнических устройств. Изменения доменной структуры, молярной концентрации х, фазового состава и направления поляризации кристаллов PMN–xPT приводят к изменениям их электромеханических свойств [4, 5] и, следовательно, могут влиять на эффективные свойства и другие важные в практическом смысле параметры композитов [3]. Кристалл PMN–0,33PT в настоящее время – единственный из ряда PMN–xPT, для которого известны полные экспериментальные наборы электромеханических констант как в монодоменном [5], так и в полидоменном (domain engineered) [4] состояниях. Монодоменный кристалл PMN–0,33PT (симметрия 3m) [5] характеризуется сочетанием больших абсолютных значений пьезомодулей  = 4100 пКл/Н и  = 1340 пКл/Н и умеренных  = –90 пКл/Н и  = 190 пКл/Н. Поляризованный полидоменный кристалл PMN–0,33PT (макроскопическая симметрия 4mm) интересен вследствие высоких значений || ~ 103 пКл/Н. Несмотря на то, что ориентационный эффект в слоистых 2–2-композитах на основе моно- и полидоменного PMN–xPT рассматривался в недавних работах [3, 6, 7], до сих пор не проводилось детального сравнения параметров родственных композитов при вращении главных кристаллографических осей кристалла (моно- или полидоменного). Настоящая работа развивает представления [3, 8-10] об анизотропных электромеханических свойствах и посвящена исследованию гидростатического пьезоэлектрического отклика новых композитов типа 2–2.
Исследуемый композит состоит из кристаллических и пористых полимерных слоев, соединенных параллельно (рис. 1). Предполагается, что эти слои бесконечно протяженны вдоль осей OX2 и OX3 и формируют регулярную структуру со

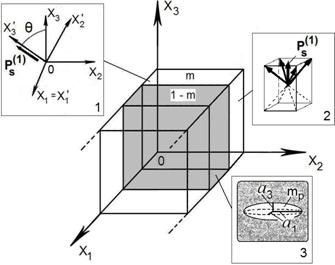
Рис. 1. Схематическое изображение 2–2–0-композита «кристалл – пористый полимер» с параллельным соединением слоев. (X1X2X3) – система координат композитного образца, (Х₁¢Х₂¢Х₃¢) – система координат, связанная с главными кристаллографическими осями кристалла. Ps(1) – вектор спонтанной поляризации кристалла, q – угол ориентации Ps(1) относительно ОX3. m и 1 – m – объемные концентрации кристаллических и полимерных слоев соответственно, mp – объемная концентрация пор в каждом полимерном слое, ai – длины полуосей пор.

связностью 2–2–0 [3]. Угол θ (вставки 1 и 2 на рис. 1) описывает поворот Ps(1) и главных кристаллографических осей кристалла в плоскости (X2OX3), параллельной границам раздела слоев. Полимерные слои композита содержат сфероидальные воздушные поры, которые регулярно распределены в полимере (связность 3–0, вставка 3 на рис. 1) и имеют одинаковые линейные размеры, значительно меньшие толщины полимерного слоя вдоль OX1. Форма пор задается в системе координат (X₁X₂X₃) уравнением (x₁ / a₁)2 + (x₂ / a₁)2 + (x₃ / a₃)2 = 1, при этом полуоси ai связаны отношением ρ = a1 / a3. Предполагается, что для поддержания стабильного монодоменного состояния кристалла (вставка 1 на рис. 1) к образцу прилагается постоянное смещающее электрическое поле.
Определение эффективных электромеханических свойств исследуемого 2–2–0-композита проводится в два этапа. На первом этапе для заданных mp и ρ определяются эффективные константы пористого полимера. При этом применяется алгоритм [11], основанный на формализме Эшелби для сфероидального включения. На втором этапе сначала определяются эффективные константы кристалла [3, 6, 7] при заданном θ, а затем по m усредняются свойства слоев (рис. 1) с учетом их электромеханического взаимодействия [3, 6]. В случае монодоменного кристалла (вставка 1 на рис. 1) угол θ варьируется в интервале [0°; 180°], а в случае полидоменного кристалла (вставка 2 на рис. 1) – в интервале
[–45°; 45°]. Последний интервал задается при условии, что векторы спонтанной поляризации всех четырех типов сегнетоэлектрических доменов (вставка 2 на рис. 1) остаются в верхней полуплоскости, т.е. над плоскостью Х₁ОХ_2.
Матрицы свойств слоев композита имеют вид

|| C(n) || = ,          (1)

где n = 1 соответствует кристаллу, n = 2 – пористому полимеру, верхний индекс “T“ обозначает транспонирование; || s(n),E ||, || d(n) || и || e(n),s || – матрицы упругих податливостей при электрическом поле E = const, пьезомодулей и диэлектрических проницаемостей при механическом напряжении s = const соответственно. Матрица эффективных электромеханических свойств 2–2–0-композита

|| C* || = [|| C(1) ||.|| M || m + || C(2) || (1 – m)] [|| M || m +
+ || I || (1 – m)]-1                                                                   (2)

определяется с учетом || C(n) || из (1) и граничных условий [12]. В формуле (2) || I || – единичная матрица, || M || – матрица, описывающая граничные условия при x1 = const, т.е. непрерывность компонент механических напряжений s11, s12, s13, механических деформаций x22, x23, x33, напряженности электрического поля E2,E3 и электрического смещения D1. Элементы матрицы (2) зависят от m, θ, mp и ρ. Эффективные свойства (2) определены в предположении, что длина волны внешней акустической волны значительно превышает толщину каждого слоя композита.
Рассмотрим концентрационные и ориентационные зависимости двух эффективных параметров композита – гидростатического пьезомодуля (ГПМ)

=                     (3)
и гидростатического коэффициента электромеханической связи (ГКЭС)

 =  / ()1/2,          (4)

где =– гидростатическая податливость при E = const. Пьезомодули , диэлектрическая проницаемость  и упругие податливости  в (3) и (4) берутся из || C* || (формула (2)), по структуре совпадающей с || C(n) || из (1). ГПМ  из (3) характеризует пьезоактивность, а ГКЭС из (4) – эффективность преобразования электрической энергии в механическую и наоборот в условиях гидростатического сжатия композита. Расчеты матрицы (2) и параметров (3), (4) проведены с использованием измеренных при комнатной температуре электромеханических констант монодоменного [5] и полидоменного [4] кристаллов PMN–0,33PT, а также полиуретана [10].
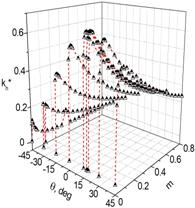
Как известно из результатов [3], присутствие в полимерных слоях сплющенных пор (ρ > 1) и увеличение их объемной концентрации mp способствуют возрастанию параметров (3) и (4) 2–2–0-композита. Примеры поведения ГПМ и ГКЭС при фиксированных параметрах ρ и mp (рис. 2) свидетельствуют о множестве экстремумов  и . Большие по модулю значения этих параметров достигаются
     
а)                                            б)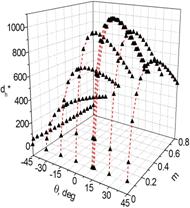
 
в)                                            г)
Рис. 2. Концентрационные (m) и ориентационные (q) зависимости гидростатического пьезокоэффициента  (a, в, в пКл / Н) и коэффициента электромеханической связи  (б, г)       2–2–0-композита «монодоменный кристалл PMN–0.33PT – пористый полиуретан» с mp = 0,3 и ρ= 10 (графики а, б) и    2–2–0-композита «полидоменный кристалл PMN–0.33PT – пористый полиуретан» с mp = 0,3 и ρ= 10 (графики в, г).

при объемных концентрациях кристалла m > 0,1, что облегчает получение соответствующих композитов.
Вследствие слоистой структуры композита (рис. 1) в области m > 0,1 значения ряда пьезомодулей  из (3) становятся соизмеримыми с  кристалла при заданной ориентации q, а присутствие границ раздела x1 = const и воздушных пор, ослабляющих пьезоэлектрический отклик вдоль оси OX1, способствует увеличению || и ||.
Корреляция между (m, θ) и (m, θ) (ср. рис. 2, a и б, а также рис. 2, в и г) объясняется важной связью между ГПМ из (3) и ГКЭС из (4). Сравнение (m, θ) и (m, θ) показывает, что достаточно слабые изменения произведения   в широких интервалах m и θ обусловливают данную корреляцию и достижение абсолютных экстремумов (m, θ) и (m, θ) при практически одинаковых углах θ. Подобное поведение параметров установлено для композитов на основе как моно-, так и полидоменного кристалла. Это поведение связано с важной ролью анизотропии упругих податливостей  пористого полимера. В частности, при ρ >> 1 отношения /, / и т.п. существенно влияют на баланс эффективных податливостей  в выражении , что в конечном счете влияет на поведение  из (4).
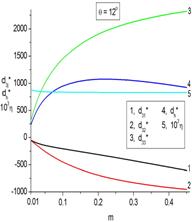
Установлено, что основной вклад в  композита на основе полидоменного PMN–0,33PT вносят пьезомодули . Несмотря на их изменения в широких интервалах (рис. 3) отношение h = (++) / » 0,80 … 0,85 остается практически неизменным вблизи абсолютного max(m, θ) и может в дальнейшем использоваться для оценок ГПМ.
Отметим, что композит на основе полидоменного кристалла PMN–0,33PT в точке абсолютного max(m, θ) = 1080 пКл/Н (см. рис. 2, в и 3, б) характеризуется следующими важными в практическом смысле параметрами: коэффициент электромеханической связи = 0,931, гидростатический пьезокоэффициент  = 82,8 мВ.м/Н, квадрат гидростатического параметра приема  = 89,8.10-12 Па-1 и ГКЭС  = 0,470. Для сравнения укажем, что монодоменный кристалл PMN–0,33PT обладает  = 0,048,  = 0,691 и  = 10 пКл/Н [5], а полидоменный кристалл PMN–0,33PT характеризуется  = 0,167,  = 0,957 и  = 160 пКл/Н [4]. В литературе отсутствуют экспериментальные данные по 2–2–0-композитам, однако имеются данные по другим связностям с пористыми полимерными компонентами. Например, в работе [13] приведены следующие гидростатические параметры     1–3–0-композита «сегнетопьезокерамика PZT – пористый полиуретан»:  = 0,11 … 0,57,  = (-1087 … 1458) пКл/Н в зависимости от микрогеометрии и объемной концентрации пор в полимере.

 
а)                                            б)
Рис. 3. Поведение пьезомодулей  и  (в пКл/Н) и фактора h  вблизи абсолютного max 2–2–0-композита «полидоменный кристалл PMN–0.33PT – пористый полиуретан» с     mp = 0,3 и ρ= 10.

Выводы
Представленные результаты указывают на важность учета ориентационных зависимостей свойств моно- и полидоменных кристаллов PMN–0,33PT при формировании гидростатического пьезоотклика исследованных 2–2–0-ком-позитов. Композиты со связностью 2–2–0 на основе моно- и полидоменных кристаллов PMN–0,33PT обладают гидростатическими параметрами, превосходящими аналогичные параметры кристаллических компонентов и композитов родственной связности. Основной вклад (около 80…85 %) в  вблизи его абсолютного максимума в случае композита на основе полидоменного PMN–0,33PT вносят пьезомодули , что представляется важным при прогнозировании поведения ГПМ родственных композитов. Полученная оценка абсолютного max = 1080 пКл/Н может стимулировать применения соответствующего композита на основе полидоменного кристалла PMN–0,33PT в гидрофонах и других гидроакустических устройствах. Значительные величины || » 0,7 … 0,8, соответствующие композиту на основе монодоменного кристалла PMN–0,33PT, представляют несомненный интерес при создании новых пьезоэлектрических преобразователей.

            Автор выражает благодарность д-ру физ.-мат. наук, проф. В.Ю. Тополову, д-ру техн. наук, проф. А.Е. Паничу (Россия), Dr. C.R. Bowen (Соединенное Королевство) и Dr. P.Bisegna (Италия) за большой интерес к проблеме исследований сегнето- и пьезоактивных материалов и полезную дискуссию. Работа выполнена при финансовой поддержке Южного федерального университета (тема НИР 11.1.09ф).

Список литературы

1. Ritter T., Geng X., Shung K.K. et al. // IEEE Trans. Ultrason., Ferroelec., a. Freq. Contr. 2000. V.47, N 4. P.792–800.
2. Cheng K.C., Chan H.L.W., Choy C.L. et al. // IEEE Trans. Ultrason., Ferroelec., a. Freq. Contr. 2003. V.50, N 9. P.1177–1183.
3. Topolov V.Yu., Glushanin S.V. // Composites Sci. a. Technol. 2009. V.69, NN 15–16. P.2532–2537.
4. Zhang R., Jiang B., Jiang W., Cao W. // J. Appl. Phys. 2001. V.90, N 7. P.3471–3475.
5. Zhang R., Jiang B., Cao W. // Appl. Phys. Lett. 2003. V.82, N 5. P.787–789.
6. Topolov V.Yu., Krivoruchko A.V. // J. Appl. Phys. 2009. V.105, N 7. P.074105–7 p.
7. Topolov V.Yu., Krivoruchko A.V. // Smart Mater. a. Struct. 2009. V. 18, N 6. P.065011–11 p
8.Тополов В.Ю., Глушанин С.В., Панич А.Е. // Нано- и микросистемная техника. 2009. N 6. C. 20–25.
9. Topolov V.Yu., Bowen C.R., Glushanin S.V., Panich A.E. // Ferroelectrics. 2009. V.393. P. 27–37.
10.Topolov V.Yu., Glushanin S.V., Bowen C.R., Panich A.E. // Sensors & Transducers. 2009. V.109, N 10. P. 108–116.
11. Dunn M.L., Taya M. // J. Am. Ceram. Soc. 1993. V.76, N 7. P.1697–1706.
12. Topolov V.Yu., Bowen C.R. Electromechanical properties in composites based on ferroelectrics. London: Springer, 2009. 202 p.
13. Gibiansky L.V., Torquato S. // J. Phys. Mech. Solids. 1997. V.45, N 5. P.689–708.