Сравнение разрешающей способности метода Прони и Бартлета при работе на фоне шумов моря
Аннотация
Дата поступления статьи: 04.12.2013Приводятся результаты сравнения ширины диаграммы направленности и коэффициента концентрации приемной антенны, рассчитанных с помощью методов Бартлета и Прони с учетом шумов взволованной поверхности моря. Показано, что эффективность оценки параметров источника сигналов с использованием метода Прони выше, чем при использовании метода Бартлета.
Ключевые слова: Метод Прони, векторно-скалярная антенна, динамический шум моря, ковариация, поток мощности
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
Сравнение характеристик методов Бартлетта и Прони
выполняется с учетом шумов, образованных взволнованной поверхностью моря. Предложенное в данной работе представление оценок параметров источника сигнала c использованием метода Прони позволило выполнить сравнении двух методов на основе общепринятых характеристик приемной антенны таких как ширина диаграммы направленности и коэффициент концентрации. Показано, что эффективность оценки параметров источника сигналов с использованием метода Прони выше, чем при использовании метода Бартлетта.
- Постановка задачи
Метод Прони является давно известным параметрическим методом восстановления квазиполинома на равномерной сетке пространственных или временных отсчетов по конечному числу его значений [1-3]. Использование этого метода для определения структуры акустического поля источника в волноводе предложена в работах [4-5]. В работе [6] изложена модификация метода Прони для оценки угловых координат источника с использованием векторно-скалярной антенны.
В данной работе рассматривается линейная эквидистантная антенна. В выбранной системе координат антенна расположена вдоль оси Х. Для гауссовых сигналов и шумов с нулевым математическим ожиданием статистика измерений полностью определяется матрицей ковариаций, которая представляет собой сумму сигнальной матрицы - ![]() =
=![]() и матрицы помех -
и матрицы помех - ![]()
![]() (1)
(1)
здесь ![]() - вектор измеряемых сигналов на приемной антенне, состоящей их М датчиков давления, P и Q – нормированные матрицы пространственной корреляции сигнала и шума, S и N – мощности сигнала и для шума, соответственно, символ «*» означает эрмитово сопряжение. Для источника, находящегося в дальней зоне приемной антенны, давление на
- вектор измеряемых сигналов на приемной антенне, состоящей их М датчиков давления, P и Q – нормированные матрицы пространственной корреляции сигнала и шума, S и N – мощности сигнала и для шума, соответственно, символ «*» означает эрмитово сопряжение. Для источника, находящегося в дальней зоне приемной антенны, давление на ![]() -ом элементе равно
-ом элементе равно
![]() , m=1,2,…,M (2)
, m=1,2,…,M (2)
Здесь ![]() - волновое число, d –расстояние между элементами антенны,
- волновое число, d –расстояние между элементами антенны, ![]() - направление на источник, которое отсчитывается от оси Х (азимут).
- направление на источник, которое отсчитывается от оси Х (азимут).
Характеристики методов Прони и Бартлетта анализируются в предположении, что приемная система работает на фоне шумов моря, при моделировании которых используется физическая модель, подтвержденная экспериментально [7]. Согласно этой модели, шумы моря создаются совокупностью независимых точечных источников, которые равномерно распределены на плоскости, параллельной свободной поверхности воды, и расположены на небольшой по сравнению с длиной волны глубине. Амплитуда излучения для всех локальных источников распределена по Релею, случайные начальные фазы равномерно распределены в интервале значений [0,2π]. Как показано в работах [8-9], при ![]() >5 достаточно использовать 4-х лучевую модель распространения сигнала в среде [10]. Метод Бартлетта является методом пространственной фильтрации со стандартным разрешением. Математически этот метод эквивалентен разложению поля, измеряемого пространственно развитой антенной, в виде суперпозиции волн, приходящих из разных точек пространства. Для плоских волн это разложение позволяет определить угловые координаты источника (азимут). Для расчета пространственного спектра выполняется Фурье – преобразование в пространственной области
>5 достаточно использовать 4-х лучевую модель распространения сигнала в среде [10]. Метод Бартлетта является методом пространственной фильтрации со стандартным разрешением. Математически этот метод эквивалентен разложению поля, измеряемого пространственно развитой антенной, в виде суперпозиции волн, приходящих из разных точек пространства. Для плоских волн это разложение позволяет определить угловые координаты источника (азимут). Для расчета пространственного спектра выполняется Фурье – преобразование в пространственной области
![]() , (3)
, (3)
здесь W – сканирующий вектор, который рассчитывается в соответствии с моделью распространения сигналов в среде (2).
Метод Прони является «быстрым» методом решения системы уравнений следующего вида:
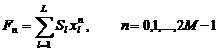 , (4)
, (4)
где ![]() — неизвестные комплексные величины (2∙L<M). Неизвестные
— неизвестные комплексные величины (2∙L<M). Неизвестные ![]() находятся как корни полинома
находятся как корни полинома
![]() , (5)
, (5)
коэффициенты которого удовлетворяют системе линейных уравнений
![]() (6)
(6)
После нахождения величин ![]() ; значения их подставляют в (4) и находят мощности
; значения их подставляют в (4) и находят мощности ![]() .
.
Применительно к линейной эквидистантой антенне измеряемые величины ![]() - это элементы строк или столбцов ковариационной матрицы (1), Значение величины
- это элементы строк или столбцов ковариационной матрицы (1), Значение величины ![]() соответствует мощности l-ого локального источника,
соответствует мощности l-ого локального источника, ![]() , где
, где ![]() — разность фаз сигнала от l-ого локального источника в двух соседних приемных элементах. Угол
— разность фаз сигнала от l-ого локального источника в двух соседних приемных элементах. Угол ![]() связан с пространственным углом прихода сигнала от l-ого локального источника соотношением
связан с пространственным углом прихода сигнала от l-ого локального источника соотношением ![]() .
.
2. Результаты моделирования
Расчеты выполнены для приемной системы, работающей в плоскопараллельном волноводе глубиной 270м с c(z)=const. Антенна расположена на глубине 220м. Локальный источник находится в дальней зоне по направлению ![]() 77º. Сигнал от локального источника моделировался как случайная величина, распределенная по нормальному закону.
77º. Сигнал от локального источника моделировался как случайная величина, распределенная по нормальному закону.
При моделировании двух методов используются одни и те же наборы входных реализаций сигнала и шума. Пространственный спектр по методу Бартлетта усреднялся по 100 реализациям. Параметры источника Sи ![]() находятся по методу Прони также по 100 реализациям. Совокупность оценок пар параметров Siи
находятся по методу Прони также по 100 реализациям. Совокупность оценок пар параметров Siи ![]() i упорядочивается в порядке возрастания найденных
i упорядочивается в порядке возрастания найденных ![]() i для построения зависимости
i для построения зависимости ![]() . Мощности сигналов, попавшие в пространственный интервал углов
. Мощности сигналов, попавшие в пространственный интервал углов ![]() =1º, суммируются. В результате такого преобразования получается аналог пространственного спектра. Это дает возможность выполнить сравнение двух принципиально различных методов с использованием общепринятых характеристик для антенн:
=1º, суммируются. В результате такого преобразования получается аналог пространственного спектра. Это дает возможность выполнить сравнение двух принципиально различных методов с использованием общепринятых характеристик для антенн: ![]() - ширины диаграммы направленности и
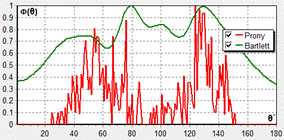
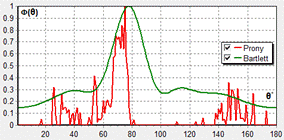
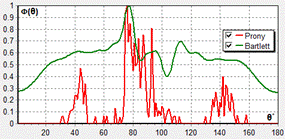
- ширины диаграммы направленности и ![]() -коэффициента концентрации. На рис.1 приведены результаты моделирования для двух рассматриваемых методов обработки при различном отношении сигнал/помеха на входе приемного элемента антенны (
-коэффициента концентрации. На рис.1 приведены результаты моделирования для двух рассматриваемых методов обработки при различном отношении сигнал/помеха на входе приемного элемента антенны (![]() 1 и 0.1) и для приемных антенн с числом приемных элементов М=11, 21 и 31. Апертура таких антенн при межэлементном расстоянии
1 и 0.1) и для приемных антенн с числом приемных элементов М=11, 21 и 31. Апертура таких антенн при межэлементном расстоянии ![]() м равны 5, 10, и 20м, соответственно. Средняя частота рабочего диапазона
м равны 5, 10, и 20м, соответственно. Средняя частота рабочего диапазона ![]() Гц.
Гц.
а б
в г
д е
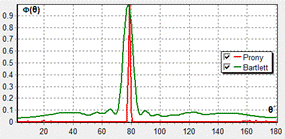
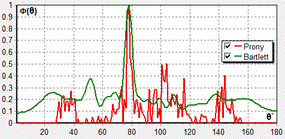
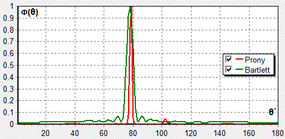
Рис.1. Пространственные спектры для метода Прони (красные кривые) и Бартлетта (зеленые кривые) при различных отношениях ![]() : а, в, д - 0.1; б, г, е – 1; и при различном числе приемных элементов в антенне:
: а, в, д - 0.1; б, г, е – 1; и при различном числе приемных элементов в антенне:
а, б -11; в, г – 21; д, е – 31.
Таблица 1
Характеристики метода Прони
М |
11 |
21 |
31 |
|||
|
|
|
|
|
|
|
|
|
|
9.7 |
0.8 |
1.47 |
7.41 |
1.96 |
5.39 |
|
|
1.27 |
0.39 |
5.35 |
0.65 |
2.97 |
0.78 |
Таблица 2
Характеристики метода Бартлетта
М |
11 |
21 |
31 |
|||
|
|
|
|
|
|
|
|
|
|
28.75 |
0.21 |
7.8 |
0.68 |
5.12 |
1.45 |
|
|
146 |
0.1 |
78.1 |
0.13 |
6.53 |
0.33 |
Из приведенных данных видно, что точность оценки координат источника сигналов при использовании метода Прони намного выше, чем для метода Бартлетта. Кроме того, уровень бокового (шумового) поля в методе Прони намного ниже, что позволяет обнаруживать источники с использованием данного метода при меньшем отношении сигнал/помеха на входе приемной системы. Данный вывод подтвержден расчетами таких характеристик как ширина диаграммы направленности по уровню 0.5 (![]() ) и коэффициент концентрации (
) и коэффициент концентрации (![]() ), которые представлены в табл.1 и табл.2. Анализ полученных данных показывает, что разрешающая способность метода Прони более чем в 10 раз превышает разрешающую способность метода Бартлетта.
), которые представлены в табл.1 и табл.2. Анализ полученных данных показывает, что разрешающая способность метода Прони более чем в 10 раз превышает разрешающую способность метода Бартлетта.
Выводы
При одной и той же сигнально - помеховой ситуации метод Прони работает более эффективно, т.к. имеет более узкий главный лепесток, как следствие направление на источник выполняется с большей точностью. Шумовой фон в пространственном спектре метода Прони практически отсутствует, что позволяет обнаруживать источник при более низких отношениях сигнал/помеха.
Литература:
1. Prony G.R.B. Essai experemenal et analytique: sur les lois de la dilitabilite de fluids elastques et sur celles de la force expanslve de la vapeure de l’eau et la vapeure de l’alkool, a differentes temperatures. //J. de L’Ecole Polytechnique. –1975. – T.1. –24-76.
2. Backer H.P. Cjmparison of FFT and Prony algorithm for bearing estimation of narrow-band signals in a realistic ocean environment. // – JASA. – Mar. – 1977. – V.61. – P. 756-762.
3.Марпл С.П. Цифровой спектральный анализ и его приложения. –М. –Мир. –1990. – 260 с.
4. Гительсон В.С., Глебова Г.М., Кузнецов Г.Н. Определение параметров коррелированных сигналов с использованием метода Прони. // Акустический журнал. – 1988. – Т.XXXIV. – 1. – 170-172/
5. Гордиенко В.А. Векторно-фазовые методы в акустике. –М.: –ФИЗМАТЛИТ, –2007. – 480 с.
6. Ларина Т.Н., Глебова Г.М., Винник Е.В. Модификация метода Прони при приеме сигналов векторно-скалярной антенной. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 1). – Режим доступа: http://ivdon.ru/magazine/archive/n4p1y2012/1094 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Cron B.F. Sherman C.H. Spatial-correlation function for various noise models // J. Acoust. Soc. Am. – 1962. – V. 34. – P.1732.
8.Шимко О.Е. , Глебова Г.М.Моделирование анизотропного шума на векторно-скалярных приемниках. [Электронный ресурс] // «Инженерный вестник Дона», 2007, №2 – Режим доступа: http://ivdon.ru/magazine/archive/n2p1y2007/504 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Глебова Г.М., Кузнецов Г.Н., Шимко О.Е. Векторно-скалярные шумовые поля, образованные взволнованной поверхностью моря // Акустический журнал, – 2013, – Т.59, №4, – 508-519.
10. Бреховских Л.М., Лысанов Ю.П. Теоретические основы акустики океана. – М.: – Наука, – 2007. – 370с.