Применение операции векторизации состояний для синтеза цифровых автоматов

Аннотация

Д.Н. Ильченко

Дата поступления статьи: 03.12.2013

Рассматривается оптимизация синтеза цифровых автоматов для решения задач поиска шаблонов с масками на ПЛИС. Это осуществляется за счет применения векторизации состояний автомата, позволяющей объединять состояния в вершины-массивы состояний. Векторизация состояний автомата упрощает логическую структуру цифрового автомата и его синтез, а также снижает количество используемых логических элементов.

Ключевые слова: цифровой автомат, граф автомата, синтез автомата, векторизация состояний автомата, программируемая логическая интегральная схема, реконфиругируемая вычислительная система, поиск шаблонов

05.13.11 - Математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей

Использование реконфигурируемых вычислительных систем (РВС) [1,2,3] для решения задач поиска шаблонов в потоке данных является одним из перспективных направлений. Одной из важнейших функций при решении подобного класса задач является возможность использования масок при формировании шаблонов. В качестве таких масок применяются специальные метасимволы ‘?’, обозначающий произвольный один символ, и ‘*’, обозначающий множество произвольных символов.

Одним из наиболее эффективных с точки зрения реализации на программируемых логических интегральных схемах (ПЛИС) и быстродействия классических алгоритмов поиска шаблонов является автоматный алгоритм Ахо-Корасик [4,5]. Однако использование масок при формировании шаблонов приведет к созданию автомата, синтез которого будет затруднен, поскольку граф такого автомата будет содержать большое количество вершин состояний автомата, для каждой из которых необходимо определить функции переходов и выходов [6]. При реализации таких автоматов на ПЛИС компиляторы систем автоматического проектирования (САПР), осуществляющие синтез автоматов, не выполняют оптимизацию графов, а лишь оптимизируют размещение элементов на кристалле, при этом все состояния автомата будут синтезированы классическим способом, при котором будут учтены все возможные функции переходов для всех состояний, представленных на графе автомата [7,8,9]. Все это усложняет синтез автомата, и использование такого автомата будет неоптимальным решением.

Необходимы новые методы, позволяющие упростить синтез таких автоматов и, по возможности, снизить используемый ресурс на их реализацию.

Метасимвол ‘*’ в маске шаблона может иметь бесконечный размер, однако в реальной жизни поиск шаблонов бесконечной длины не является актуальной задачей. Поэтому более осмысленным и целесообразным является поиск шаблонов, содержащих [1..m] символов в маске. Это будет равносильно замене шаблона с ‘*’ на множество шаблонов, включающих в себя следующий набор масок *[1..m] = {?₁, ?₁?₂, ?₁?₂?₃, ... , ?₁?₂?₃..?_m}. Также возможны более сложные комбинации при задании масок в шаблонах. Например, ‘*’ может определяться как набор [n..m], где n – минимальное количество любых символов шаблона, m – максимальное количество любых символов шаблона, при этом m > n.  Такая запись подразумевает возможность попадания в шаблон любых символов в количестве от n до m.  Это будет равносильно замене ‘*’ на комбинации шаблонов, включающих в себя следующий набор масок *[n..m] = {?₁...?_n, ?₁...?_n+1,..., ?₁..?_m}.

Очевидно, что использование таких масок в шаблонах приводит к избыточности графа автомата, решающего задачу поиска шаблонов. При этом автомат содержит множество состояний, функции переходов между которыми являются идентичными, но сами состояния не являются эквивалентными. Такая избыточность графа усложняет логическую структуру автомата и, следовательно, усложняется его синтез, поскольку каждому такому состоянию автомата необходимо определять функцию перехода и функцию выхода.

Эффективная разработка цифрового автомата, решающего задачу поиска шаблонов с масками ‘*’ и ‘?’, заключается прежде всего в минимизации затрат на логическую структуру автомата, что приводит к упрощению его синтеза.

Задачу поиска большого числа шаблонов можно решить двумя способами. Первый способ – это реализация тривиального метода (наивный алгоритм или алгоритм "грубой силы" [10]), который заключается в прямом сравнении шаблона и входного потока данных. Фактически такая реализация будет представлять собой некоторый автомат, состоящий из множества недетерминированных автоматов, каждый из которых в темпе поступления входных воздействий осуществляет поиск отдельного шаблона. Такой вариант будет неоптимальным, поскольку объем ресурса на его реализацию, а именно, количество регистров, будет находиться в прямой зависимости от количества состояний.

Вторым способом является построение автомата, который будет менять свои состояния в зависимости от входных воздействий, при этом количество регистров на хранение и кодирование состояний будет определяться по формуле

  N = ]log₂M[                (1)

где M – количество возможных состояний автомата.

Этот метод является более предпочтительным с точки зрения аппаратных затрат, однако использование масок усложняет синтез такого автомата.

Для упрощения синтеза цифрового автомата, решающего задачу поиска шаблонов с масками, применяется операция векторизации состояний автомата. Применение векторизации позволяет провести декомпозицию структуры автомата и вынести часть состояний автомата из основного графа, объединив эти состояния в вершины-массивы состояний. При этом автомат разбивается на группу автоматов. Операция векторизации дает возможность упростить реализацию автомата.

Основная идея метода векторизации состояний автомата заключается в том, что в исходном графе определяются вершины, соответствующие состояниям автомата, в которые он последовательно переходит при любых входных воздействиях. Например, это состояния автомата, соответствующие маске шаблона, которая подразумевает под собой группу любых символов, в данном случае не важно, в какое состояние перейдет автомат при попадании в маску шаблона, важно лишь условие, которое выведет автомат в строго определенное состояние, соответствующее конкретно-определенному символу шаблона, либо переведет автомат в начальное состояние. Такие состояния автомата заменяются вершиной-массивом состояний. При переходе автомата в вершину-массив состояний управление состояниями осуществляется некоторым управляющим автоматом, например, счетчиком, состояния которого соответствуют состояниям автомата в вершине-массиве. После перехода управляющего автомата в конечное состояние формируется сигнал выхода из вершины-массива, либо в процессе перехода по состояниям управляющего автомата и определенного входного воздействия, которое соответствует символу шаблона после маски, формируется сигнал перехода из вершины-массива состояний в следующую вершину.

Метод векторизации состояний автомата не уменьшает количество его состояний, но при этом существенно упрощается его структура, поскольку множество последовательных состояний автомата, имеющих идентичные функции переходов, будет объединено в одну вершину-массив состояний.

Следует отметить, что при использовании *[0,∞) в маске шаблона наиболее эффективным является использование всего одного состояния автомата – состояния ожидания автомата. В этом случае при переходе в состояние, соответствующее данной маске шаблона, автомат ожидает на входе следующего значимого символа после маски. Однако такой вариант шаблона в реальной жизни не актуален и не имеет никакого смысла, ведь шаблоны, как правило, имеют некоторый конечный размер, а поиск бесконечного шаблона может привести к неопределенности и зацикливанию программы. Корректное использование маски ‘*’ должно подразумевать либо некоторый конечный размер символов в маске, либо задание маски граничными значениями.

В качестве примера рассмотрим шаблон "a*b", где *[1..10]. Граф автомата для поиска этого шаблона представлен на рис.1. Синтез автомата, представленного данным графом и решающего задачу поиска довольно простого шаблона, сложен, поскольку необходимо определить функции переходов, функции возвратов и выхода для тринадцати вершин графа, соответствующих состояниям автомата.

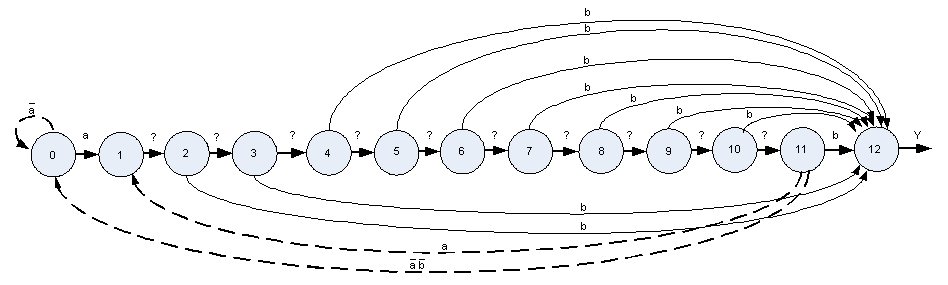
Рис. 1. – Невекторизированный граф автомата поиска шаблона

Применяя операцию векторизации состояний, автомат будет представлен в виде подграфа, в котором счетчик выполняет функцию автомата управления. Векторизированный граф автомата поиска шаблона - "a*b", где *[1..10] показан на рис.2.

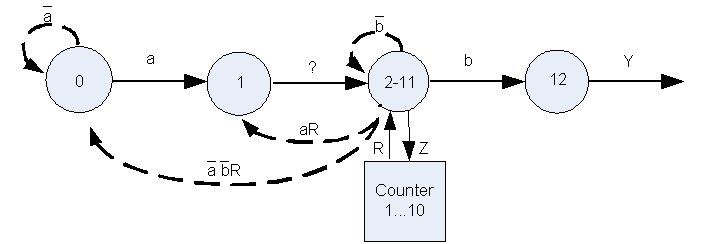
Рис. 2 – Векторизированный граф автомата поиска шаблона

Вершины 2,3,4,...11, представленные на невекторизированном графе, заменяются вершиной-массивом состояний с номером 2-11. Переход в эту вершину передает управление счетчику, и дальнейшие состояния автомата определяются состояниями этого счетчика. Диапазон работы счетчика соответствует количеству состояний в вершине-массиве, т.е. 1..10. При значении счетчика, равном 10, формируется выходная функция R.

Очевидно, что синтез такого подграфа будет проще, поскольку необходимо задать функции переходов, возвратов и выхода только для 4-х вершин графа, одна из которых будет являться вершиной-массивом состояний. Синтез счетчика тривиален и не зависит от графа основного автомата. Общее количество состояний автомата при векторизации не меняется.

Таким образом, векторизация состояний автомата не снижает общего количества состояний, но за счет объединения состояний в вершину-массив состояний упрощается адресация к этим состояниям и, следовательно, синтез автомата становится проще.

Для оценки эффективности метода векторизации состояний с точки зрения используемого количества триггеров и логических элементов («И» и «ИЛИ»), выведем формулу оценки ресурсов. Необходимое количество логических элементов при синтезе автомата можно оценить как

L ≈ 2 ⋅ M,                    (2)

где M – количество возможных состояний автомата.

Количество триггеров, необходимых для хранения и кодирования M состояний, определяется по формуле (1). Формулы (1) и (2) используются при оценке невекторизированного графа.

При оценке векторизированного графа автомата используемое количество триггеров и логических элементов будет определяться совокупностью элементов и триггеров основного автомата и счетчика, выступающего в роли управляющего автомата.

Синтез счетчика [11] является тривиальной задачей. Количество используемых триггеров определяется по формуле (1), а количество логических элементов определяется количеством триггеров счетчика и дополнительно 2-х логических элементов на реализацию функции выхода и функции инициализации счетчика. При этом количество состояний счетчика соответствует количеству состояний в вершине-массиве состояний и определяется как количество символов в маске шаблона, т.е. M_счет. = K_вект.

В общем случае количество логических элементов, используемых для реализации синтезируемого автомата, будет определяться по формуле

L ≈ 2 ⋅ (M_общ. - M_вект.) + (]log₂M_счет.[+2),                (3)

где M_общ. – общее количество состояний невекторизированного автомата,

M_вект. – количество состояний, объединенных в вершину-массив состояний, с учетом замены этих состояний одной вершиной в графе,

M_счет. – количество состояний счетчика управления.

Количество триггеров, используемых для хранения и кодирования состояний, в общем виде может быть рассчитано по формуле

N = ]log₂(M_общ. - M_вект.[ + ]log₂M_счет.[.                (4)

При использовании формул (3) и (4) для оценки невекторизированного графа составляющие счетчика и M_вект. не учитываются.

Если выразить состояния автомата и счетчика через общее количество символов в шаблоне K_общ. и количество символов в маске шаблона K_вект., то формулы (3) и (4) будут выглядеть следующим образом:

L ≈ 2 ⋅ (K_общ. - K_вект. + 2) + ]log₂K_вект.[+2

  N = ]log₂(K_общ. - K_вект. + 2[ + ]log₂K_вект.[

График количества используемого ресурса в зависимости от степени векторизации графа при фиксированном размере шаблона представлен на рис. 3.

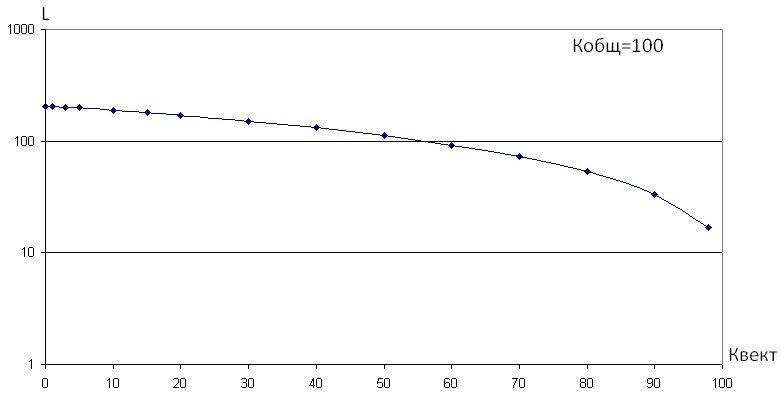
Рис. 3 – График зависимости количества логических элементов от степени векторизации состояний автомата при его синтезе

Для примера шаблон задан как "a*b", размер шаблона K_общ. = 100. При K_вект. = 0 граф не векторизирован. Минимальное количество векторизируемых вершин определим равным K_вект.= 3, максимальное – K_вект.= 98, т.е. при минимальной степени векторизации - *[1..3], при максимальной - *[1..98].

При минимальной степени векторизации состояний автомата количество используемых логических элементов практически неизменно, но с увеличением степени векторизации количество элементов логики существенно уменьшается.

Метод векторизации состояний автомата упростил синтез автомата, а также позволил существенно сократить количество используемых логических элементов. Таким образом, данный метод может быть эффективно применен при синтезе автоматов для решения задач сигнатурного анализа, например, при реализации аппаратного антивируса.

Литература:

1. Каляев А.В., Левин И.И. Модульно-наращиваемые многопроцессорные системы со структурно-процедурной организацией вычислений. - М.: Янус-К, 2003. – 380 с.

2. Строцев А.А., Андреев А.А. Оценка нахождения реконфигурируемой вычислительной системы в состояниях эффективного функционирования [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p1y2012/1212 (доступ свободный) – Загл. с экрана. – Яз. рус.

3. Андреев А.А. Методика выбора базовой архитектуры реконфигурируемой вычислительной системы на основе методов теоретико-игровой оптимизации [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1 – Режим доступа: http://ivdon.ru/magazine/archive/n1y2013/1569 (доступ свободный) – Загл. с экрана. – Яз. рус.

4. Alfred V. Aho and Margaret J. Corasick Efficient String Matching: An Aid to Bibliographic Search [Электронный ресурс] // Режим доступа: http://www.ece.ncsu.edu/asic/ece792A/2009/ECE792A/Readings_files/p333-aho.pdf (доступ свободный) – Загл. с экрана. – Яз. англ.

5. Гасфилд Д. Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология / Пер. с англ. И.В. Романовского. — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с.

6. Поликарпова Н.И., Шалыто А.А. Автоматное программирование - СПб.: СПбГПУ, 2008. - 227с.

7. Строганов А. Проектирование комбинационных схем в базисе ПЛИС [Электронный ресурс]   // «Компоненты и технологии», 2008, №5 – Режим доступа: http://www.kit-e.ru/articles/plis/2008_5_148.php (доступ свободный) – Загл. с экрана. – Яз. рус.

8. Соловьев В., Климович А. Синтез на ПЛИС совмещенных моделей конечных автоматов [Электронный ресурс]   // «ChipNews», 2003, №3 – Режим доступа: http://www.chip-news.ru/archive/chipnews/200303/4.html (доступ свободный) – Загл. с экрана. – Яз. рус.

9. Соловьев В. Структурные модели конечных автоматов при их реализации на ПЛИС [Электронный ресурс]   // «ChipNews», 2002, №9 – Режим доступа: http://www.chip-news.ru/archive/chipnews/200209/1.html (доступ свободный) – Загл. с экрана. – Яз. рус.

10. Apostolico A., Galil Z. Pattern Matching Algorithms – New York: Oxford University Press; 1997. – 377 p.

11. Глушков В.М. Синтез цифровых автоматов – М.: Физматгиз; 1962. – 476 с.