Формирование точного автомодельного решения задачи гидродинамического расчета упорного подшипника, обладающего повышенной несущей способностью и демпфирующими свойствами, работающего на двуслойной смазке в нестационарном режиме трения
Аннотация
Дата поступления статьи: 10.12.2013В данной работе дается метод формирования точного автомодельного решения задачи гидродинамического расчета упорного подшипника с адаптированным профилем опорной поверхности и обладающего демфирующими свойствами в нестационарном режиме трения. Получены и проведены оценки основных рабочих характерестик: безразмерной несущей способности, безразмерной силы трения и безразмерных расходов. Получены оптимальные параметры для основных рабочих характеристик.
Ключевые слова: упорный подшипник, двухслойная смазка, пористый слой, нестационарная задача.
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Как уже было отмечено в работе [1], при взаимодействии на границе раздела жидкости с твердой опорной поверхностью подшипника, происходит образование пристенного слоя жидкости другой вязкости, отличной от вязкости смазок в основном слое. В работе [1] в отличие от других работ, посвященных данной проблеме при анализе основных характеристик, режим течения в смазочном слое считался нестационарным. Однако, недостаток предыдущей работы заключался в том, что подшипник не обладал демпфирующими свойствами, поверхности подшипника являлись сплошными. Так как большинство пар трения работают в нестационарном режиме трения, поэтому разработка расчетной модели подшипников скольжения в нестационарном режиме трения с учетом сил инерции и демпфирующих свойств подшипника является актуальной задачей трибологии, непосредственно связанной с анализом устойчивости работы подшипника.
В данной статье, предложенный в работе [1] метод расчета основных рабочих характеристик подшипника обобщается на случай, когда на направляющей поверхности подшипника присутствует пористый
Постановка задачи. Начальные и граничные условия.
Рассматривается неустановившееся стратифицированное течение двухслойной вязкой несжимаемой жидкости в зазоре упорного подшипника скольжения с адаптированным профилем опорной поверхности.
Предполагается, что ползун неподвижен, а шип с пористым слоем движется в сторону сужения зазора с заданной скоростью u* , на которую накладываются возмущения![]()
![]() , где
, где ![]() - амплитуда,
- амплитуда, ![]() - частота возмущения (рис.1).
- частота возмущения (рис.1).
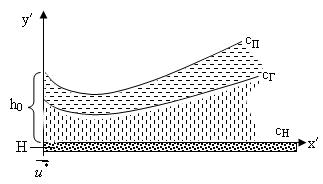
Рис. 1 Схематическое изображение двухслойной смазки в зазоре упорного подшипника при наличии пористого слоя на поверхности направляющей
В декартовой системе координат ![]() уравнение адаптированного контура CП ползуна, границы раздела СГ, а также направляющей СН с пористым слоем толщины Н, имеют вид:
уравнение адаптированного контура CП ползуна, границы раздела СГ, а также направляющей СН с пористым слоем толщины Н, имеют вид:
![]() (1)
(1)
Здесь ![]() соответственно амплитуда и частота контурных возмущений, характеризующих степень отклонения контура ползуна от прямолинейного,
соответственно амплитуда и частота контурных возмущений, характеризующих степень отклонения контура ползуна от прямолинейного, ![]() ,
, ![]() начальный зазор;
начальный зазор; ![]() - угловой коэффициент линейного контура.
- угловой коэффициент линейного контура.
В дальнейшем ![]() определяется из условия максимума несущей способности подшипника,
определяется из условия максимума несущей способности подшипника, ![]() одного порядка малости, где l – длина ползуна.
одного порядка малости, где l – длина ползуна.
В качестве основных уравнений, по аналогии с [2,3], в расчётах берутся безразмерная нестационарная система уравнений движения вязкой несжимаемой жидкости для случая «тонкого слоя», уравнения неразрывности и уравнение Дарси(в пористом слое режим считается квазистационарным):
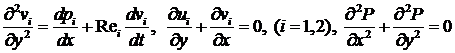 (2)
(2)
где размерные величины ![]() в смазочном слое связаны с безразмерными
в смазочном слое связаны с безразмерными ![]() соотношениями
соотношениями
![]()
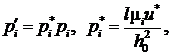
![]() ,
, ![]() (3)
(3)
Здесь ![]() - компоненты вектора скорости,
- компоненты вектора скорости, ![]() - гидродинамическое давление в смазочных слоях,
- гидродинамическое давление в смазочных слоях, ![]() - динамический коэффициент вязкости.
- динамический коэффициент вязкости.
В пористом слое переход к безразмерным переменным осуществляется по формулам: ![]() (4)
(4)
где ![]() - гидродинамическое давление в пористом слое.
- гидродинамическое давление в пористом слое.
Граничные условия на поверхности ползуна и направляющей записываются в виде:
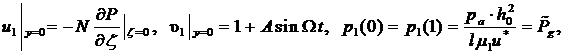
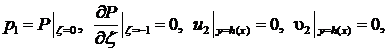
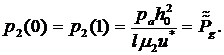 (5)
(5)
На границе раздела слоёв
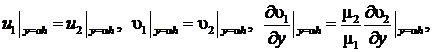
 (6)
(6)
![]() - проницаемость пористого слоя.
- проницаемость пористого слоя.
Граничные условия (5) означают прилипание смазки к поверхности ползуна и направляющей, а также, что переходя через пористую поверхность, давление меняется непрерывно, а нормальная составляющая скорости определяется законом Дарси.
Помимо этого, на непроницаемой поверхности направляющей нормальная составляющая скорости равна нулю. Давление в начальном и конечном сечениях равно атмосферному.
Условия (6) означают: условие существования слоистого течения смазки, т.е. требуется, чтобы скорость точек границы раздела слоёв в каждой точке была направлена по касательной к контуру раздела слоёв, а также равенство скоростей, касательных и нормальных напряжений на границе раздела слоев.
Полагая толщину пористого слоя достаточно малой, осредним уравнение Дарси по толщине этого слоя
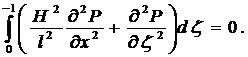 (7)
(7)
Точное автомодельное решение системы уравнений (2), удовлетворяющее граничным условиям (5) и (6), с учётом (7), будем искать в виде:
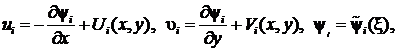
![]()
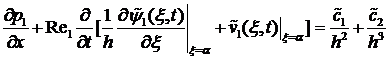

![]() (8)
(8)
Подставляя (8) в (2) и в граничные условия (5) и (6), с учётом (7), будем иметь: ![]() ,
,  ,
, 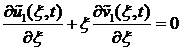 ,
, ![]() ,
,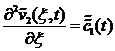 ,
, ![]() ; (9)
; (9)

![]()
![]()
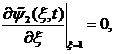
![]()
![]()
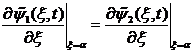 ,
, ![]() ,
,![]() ,
,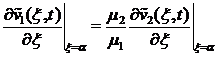 ,
, 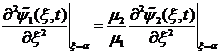 ,
,![]() ,
,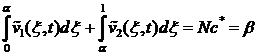 . (10)
. (10)
Решение задачи (9) – (10) находится непосредственным интегрированием.
Для определения постоянных ![]()
![]() придём к алгебраической системе, которая сводится к матричному уравнению вида:
придём к алгебраической системе, которая сводится к матричному уравнению вида:
![]() где
где ![]()
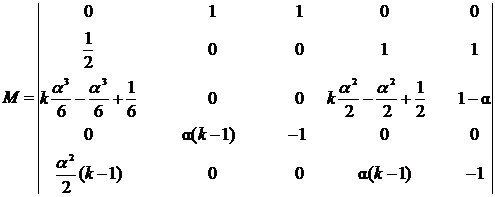
Выражения, полученные для постоянных ![]()
![]() в работе не приводятся в виду их громоздкости.
в работе не приводятся в виду их громоздкости.
Безразмерные расходы Q1 и Q2 двухслойной смазочной жидкости определяются выражениями:
![]() ,
, ![]() .
.
Безразмерная поддерживающей сила ![]() и безразмерная сила трения
и безразмерная сила трения ![]() , определяются выражениями:
, определяются выражениями:
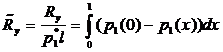
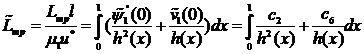
Результаты численного анализа полученных аналитических выражений для основных рабочих характеристик, показывают:
1. С увеличением вязкостного отношения, несущая способность возрастает.
2. С уменьшением параметра α, характеризующего протяженность слоев, при k>1, несущая способность увеличивается.
3. С увеличением параметра ![]() , несущая способность уменьшается, при этом для значений
, несущая способность уменьшается, при этом для значений ![]() теряется устойчивость.
теряется устойчивость.
4. При ![]() ,
, ![]() ,
, ![]() с ростом
с ростом ![]() , несущая способность увеличивается.
, несущая способность увеличивается.
5. С ростом ![]() безразмерный расход
безразмерный расход ![]() увеличивается,
увеличивается, ![]() - уменьшается.
- уменьшается.
6. С уменьшением параметра k, увеличением параметра ![]() , уменьшением
, уменьшением ![]() , при
, при ![]() -сила трения увеличивается.
-сила трения увеличивается.
7. С ростом параметра k, ростом ![]() -безразмерный расход
-безразмерный расход ![]() -увеличивается, а безразмерный расход
-увеличивается, а безразмерный расход ![]() - уменьшается.
- уменьшается.
![]()
![]()
![]()
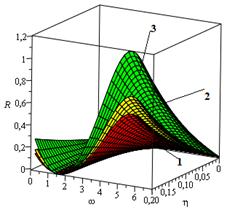
Рис. 2 Зависимость безразмерной несущей способности от параметров ω и η при разных значениях параметров α , k и Re1
![]()
![]()
![]()
![]()
![]()
![]()
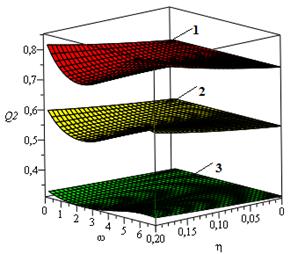
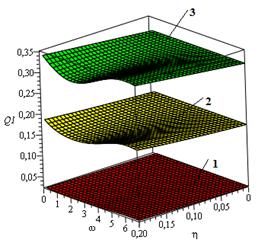
Рис.3 Зависимость расхода Q1 от Рис.4 Зависимость расхода Q2 от
параметров ω и η при разных параметров ω и η при разных
значениях параметров α , k и Re1 значениях параметров α , k и Re1
Литература:
1. Айзинбуд А.К. Разработка метода гидродинамического расчета упорного подшипника, работающего на двухслойной смазке в нестационарном режиме трения.//Вестник РГУПС №3,2013.-С. 170-177
2. Ахвердиев К.С., Александровна Е.Е., Мукутадзе М.А, Стратифицированное течение двухслойной смазки в зазоре упорного подшипника, обладающего повышенной несущей способностью и демпфирующими свойствами//Проблемы синергетики в трибологии, трибоэлектрохимии, материаловедении и мехатронике: материалы VIII Междунар. науч.-практ. конф. /ЮРГТУ- Новочеркасск, 2009.- С.14-22.
3. Александровна Е.Е., Мукутадзе М.А., Копотун Б.Е., Математическая модель двухслойной смазки в зазоре упорного подшипника, обладающего повышенной несущей способностью и демпфирующими свойствами //Труды Международной научно-практической конференции «Проблемы и перспективы развития транспортного комплекса: образование, наука, производство» - Ростов н/Д , 2009.- С.8-9.
4. Ахвердиев К.С., Воронцов П.А., Черкасова Т.С., Гидродинамический расчет подшипников скольжения с использованием моделей слоистого течения вязкой смазки//Трение и износ. 1998.- Т.16, №6-С 698-707
5. Фукс Г.И., Кутейникова З.А., Блехеров М.М., О двухслойной смазке// Вуз сб.: Исследования по физикохимии контактных взаимодействий. Уфа: Башиздат, 1971.-с.79-93.
6. Коровчинский М.В., Теоретические основы работы подшипников скольжения. М., Машгиз., 1959.-403с
7. Raimondi A.A. An adiabatic solution for the finite slider bearing.- Trans. ASLE , 1966.-V.9,3,-P.283-286.
8. Ахвердие К.С., Александрова Е.Е., Кручина Е.В., Мукутадзе М.А., Стратифицированное течение двухслойной смазки в зазоре упорного подшипника, обладающего повышенной несущей способностью///Вестник Дон. Гос.техн. ун-та-2010. - Т.10 №2(45). -С.217-223.
9. Мукутадзе М.А., Флекс Б.М., Задорожная Н.С., Полчков Е.В., Мукутадзе А.М., Расчетная модель гидродинамической смазки неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения при наличии принудительной подачи смазки [Электронный ресурс] // «Инженерный вестник Дона», 2013 г., №3 – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1765 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Gear C.W. Numarical Initial Value Problems in Ordinary Differential Equations / Prentice-Hall, Inc., Englewood Cliffs. - N.J., 1972. – С. 52.
11. Баранова Д.А., Математическая модель деформирования подкрепленных оболочек вращения при учете различных свойств материала [Электронный ресурс] // «Инженерный вестник Дона», 2012 г., №2 – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2012/745 (доступ свободный) – Загл. с экрана. – Яз. рус