Системотехника оптимального проектирования элементов строительных конструкций
Аннотация
Дата поступления статьи: 07.01.2014Показаны возможности использования методов математического программирования для получения оптимальных решений строительных конструкций. В качестве оптимизационного алгоритма использован метод частной оптимизации, основанный на свойстве монотонности используемых зависимостей. Подчеркивается целесообразность применения методов математического моделирования при обеспечении комплексной безопасности строительных объектов и уменьшения риска наступления отказа.
Ключевые слова: оптимальное проектирование, математическое моделирование, комплексная безопасность, частная оптимизация, листовые конструкции, риск.
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Опыт использования системотехники в различных направлениях инженерной деятельности, а также развитие системотехники строительства позволяет определить в качестве одной из областей ее применения исследование проблем проектирования. Большинство современных проблемы строительства можно отнести к системотехническим с условным разделением на следующие группы: технические, организационные, экономические, плановые и управленческие [1, 2, 3, 4, 5, 6]. К одной из технических проблем проектирования относится задача выбора оптимального проектного решения сложных строительных объектов.
Оптимизация проектных решений является одним из элементов технического проектирования. Эта процедура позволяет инженерам либо найти оптимальные геометрические и технические характеристики объекта при заданных условиях, либо вывести общие соотношения и построить необходимые методы расчета, если их еще не существует [7]. При этом процесс оптимального выбора основных характеристик проектируемого объекта становиться частью соответствующего метода решения задачи, а оптимизация проектных решений остается содержательной основой проектирования.
Цель поиска оптимального решения заключается в том, чтобы при проектировании объекта подобрать такие параметры и характеристики, которые с определенной точки зрения будут наилучшими [8]. При этом одним из основных подходов для решения оптимизационных задач является метод моделирования. Согласно одного из определений, моделирование является методом изучения объекта исследования путем построения соответствующих моделей, а математическое моделирование – исследование физического объекта путем создания его математической модели и оперирования ею с целью получение полезной информации о физическом объекте [1].
При решении практических задач строительного проектирования, выбор проектных решений часто основывается на инженерном опыте и интуиции. Однако, когда решение задач проектирования базируется на численном оптимизационном алгоритме, инженерная проблема может рассматриваться как чисто математическая. При этом подбор проектных решений полагается на итерационный оптимизационный процесс численных данных.
Для решения задачи оптимального проектирования используем метод математического моделирования. Исследование объектов с помощью этого метода позволяет проникнуть в сущность изучаемых объектов и дает возможность решения многокритериальных задач.
Одним из методов математического моделирования является предложенный Уайлдом метод последовательной частной оптимизации [7], используемый при решении инженерных задач, в случае, когда в задаче имеется несколько переменных. Суть метода заключается в том, что несколькими переменными оперируют поочередно, а не одновременно т.е. на каждом этапе оптимизация производится лишь для одной из переменных [9], при этом используется свойство монотонности функций, которое преобладает в инженерных задачах по оптимизации конструкций.
Решим задачу выбора оптимальных размеров для горизонтального цилиндрического резервуара высокого давления для хранения сжиженного газа. Объем резервуара примем
, внутреннее давление
;
Имеем следующие переменные: 
– толщина стенки; 
– внутренний радиус; 
– длина резервуара; 
– толщина днища.
На первом этапе решения задачи определим. как меняется стоимость днища 
в зависимости от переменных 
.
Общая стоимость изготовления резервуара зависит от 
,
,
,
, т.е. необходимо минимизировать функцию стоимости 
. Рассматриваем 
и определяем, что меняется в стоимости объекта в зависимости от изменения 
. Очевидно, что в первую очередь меняется стоимость днища. Поскольку стоимость днища зависит вообще от объема 
стали умноженный на стоимость стали, при этом стоимость стали принимается постоянной, значит стоимость днища меняется в зависимости от объема стали 
переменных 
и 
Соответственно имеем стоимость днища
– функция от радиуса и толщины.
Так как общая стоимость резервуара достигает минимума, когда минимизировано днище по 
, то возможные значения других переменных на данном этапе оптимизации не рассматриваем.
Примем, что нижняя граница для функции 
при постоянном 
, может быть определена как 
, т.е. 
– частный минимум функции по 
, т.е. мы меняем только 
. Процесс определения 
называется частная оптимизация по переменной 
.
Общую стоимость резервуара представим в виде суммы стоимости днища 
и стоимости стенки 
причем стоимость стенки не зависит от 
.
Рассматриваем весь объект относительно первой переменной 
. Последовательная частная минимизация общей стоимости резервуара относительно 
, состоит в том, чтобы найти
т.к. функция 
не зависит от 
.
В представленном уравнении частный минимум общей стоимости зависит от всех переменных задачи, кроме 
, поскольку 
– минимизируемая переменная и значение этой переменной оптимизируется вне оптимизации функции общей стоимости.
В конечном счете нас интересует минимизация общей стоимости резервуара по всем четырем переменным, что может быть записано как:
(1)
Требуемый результат можно получить определив частный минимум по 
и минимизируя полученную функцию по всем остальным переменным. Последовательность этих операций представляется как:
(2)
Два минимума функции общих затрат (1) и (2) должны быть равны между собой.
Правая часть данного уравнения указывает на то обстоятельство, что исходную задачу, включающую четыре переменные, следует решать на первом этапе путем частной оптимизации по 
.
Для этого достаточно исследовать функцию, характеризующую стоимость днища и установить ограничение по 
вида 
.
Согласно Справочнику проектировщика [10] сферические днища рассчитываются на прочность по формуле:
, откуда 
Примем 
, тогда
Для стали марки 09Г2С-15 (С345) при толщине 
; 
;
– коэффициент условия работы;
– коэффициент надежности по нагрузке для внутреннего давления.
Получим 
Задача последовательной частной оптимизации состоит в определении 
с учетом ограничения (условий прочности для днища). При этом радиус 
временно принимается как постоянная величина, а 
– как параметр, который может принимать соответствующие значения для различных проектных характеристик.
Стоимость днища пропорциональна объему металла и является возрастающей функцией от 
, которая имеет вид.
Объем стали днища 
,
Обозначим константу 
как параметр стоимости днища 
,
Таким образом,
,
Следовательно,
, поэтому для минимизации стоимости днища необходимо его толщину 
сделать как можно меньше, т.е. как можно ближе к нижней границе 
.
Таким образом, минимальная стоимость днища равна:
,
где 
– является параметром.
На следующем этапе решения задачи проведем частную оптимизацию общей стоимости резервуара по толщине стенки 
.
Про прочих равных условиях 
стоимость изготовления стенки резервуара увеличиваются при увеличении 
. Поэтому значение 
необходимо сделать как можно меньшим. Установим ограничение прочности на стенку резервуара. Согласно [10] напряжение в стенке резервуара составит:
,
где 
– расчетное сопротивление сварного шва при физических методах контроля;
– коэффициент условия работы;
– коэффициент надежности по назначению;
– коэффициент надежности по нагрузке для внутреннего давления;
– толщина стенки;
Представим накладываемое ограничение в виде 
, где
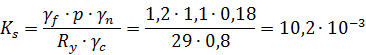
Функция стоимости стенки резервуара достигает минимума, когда величина 
соответствует точной нижней границе т.е. 
,
Таким образом,
Стоимость материала стенки пропорциональна его объему, который равен 
. Обозначим 
– параметр стоимости стенки.
Имеем 
Минимизируя 
подставим 
, тогда стоимость резервуара минимизируется по 
и составит
- является возрастающей функцией от 
и 
.
Итог частной оптимизации двух переменных будет выглядеть в виде:
(3)
Для того, чтобы осуществить минимизацию по 
и по 
, необходимо рассмотреть оставшиеся ограничения.
Объем резервуара составит:
(4)
Видно, что функции (3) и (4) при увеличении 
и 
возрастают. Соответственно, чем больше объем резервуара, тем больше его стоимость. Резервуар минимально допустимого объема 
соответствует минимальной стоимости.
Из уравнения объема резервуара можно получить явное выражение для 
, при этом 
– неизвестно.
Исключение 
из соотношения (3) приводит к зависимости:
,
- мы получили уравнение с 
в первом слагаемом.
Поскольку коэффициент 
является положительным, а коэффициент 
не зависит от 
, то общая стоимость резервуара представляет собой возрастающую функцию величины 
. Соответственно, радиус резервуара должен быть как можно меньше. В то же время из формулы объема резервуара 
видно, что величина радиуса ограничена снизу, т.к. существует верхняя граница длины стенки – максимальное значение 
.
; 
Соответственно принимаем 
, где 
- значение данной переменной при которой достигается минимум оптимизируемой функции.
У нас имеется два ограничения на толщину днища 
, нижняя граница определяется условием прочности, верхняя граница – ограничением общей длины резервуара 
. Так как с ростом 
стоимость днища увеличивается, то в точке минимума в качестве активного ограничения должна использоваться точная нижняя граница, т.е. 
. Для частной оптимизации по 
требуется использовать в качестве активного ограничения предельную величину объема резервуара 
.
Таким образом. имеются четыре ограничения:
- для толщины стенки 
;
- для толщины днища 
;
- для размеров, определяющих объем 
;
- для общей длины резервуара 
.
Окончательно имеем, что определение оптимального проектного решения обеспечивается использованием следующих уравнений:
- оптимальное значение длины резервуара 
;
- оптимальное значение радиуса стенки 
;
- оптимальное значение толщины днища 
;
- оптимальное значение толщины стенки.
В рассматриваемом примере заданы следующие основные проектные характеристики
; 
; 
; 
,
Тогда переменные имеют следующие оптимальные значения.
;
. Что соответствует 
– следовательно выполняется ограничение по соблюдению транспортного габарита.
;
.
Вывод.
Рассмотренный в статье метод частной оптимизации позволяет находить оптимальные параметры листовых конструкций. При решении задачи оптимизирования накладывались следующие ограничения: максимальная длина определяется условиями транспортного габарита резервуара, толщина днища и стенки определяются требованиями норм проектирования исходя из условия прочности. При этом каждое ограничение рассматривается как строгое равенство.
Резервуары для хранения сжиженных газов относятся к объектам повышенной опасности, что требует анализа работы конструкции с использованием научных методов. Применение методов математического моделирования при оптимальном проектировании конструкции позволяет снизить вероятность отказа и разрушения, а также уменьшить риск экологического и материального ущерба.
Литература:
1. Системотехника [Текст] / Под. ред. А.А.Гусакова. -М.: Фонд «Новое тысячелетие», 2002. -768 с.
2. Гуд Г.-Х. Системотехника. Введение в проектирование больших систем, пер. с англ. [Текст] / Г.-Х. Гуд, Р.-Э. Макол. -М., 1962. -357 с.
3. Касьянов В.Е., Котесов А.А., Котесова А.А. Аналитическое определение параметров закона Вейбулла для генеральной совокупности конечного объема по выборочным данным прочности стали [Электронный ресурс] // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2012/804 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Холкин Д.В. Системная инженерия - новая профессия для новой энергетики [Текст] / Д.В. Холкин // Энергоразвитие. -2010. -№3(13). –С.45-48.
5. Tippet. The Methods of statistics [Текст], J.,Wiley, N.J. -394 р.
6. Касьянов В.Е., Щулькин Л.П., Котесова А.А., Котова С.В. Алгоритм определения параметров прочности, нагруженности и ресурса с помощью аналитического перехода от выборочных данных к данным совокупности [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1236 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Уайлд Д. Оптимальное проектирование: Пер. с англ. [Текст] / Д. Уайлд. -М.: Мир, 1981. -272 с.
8. Сидоров В.Н. Математическое моделирование в строительстве. Учебное пособие [Текст] / В.Н.Сидоров, В.К. Ахметов. -М.: Изд-во АСВ, 2007. -336 с.
9. Yeh-Liang Hsu. Developing a fuzzy proportional-derivative controller optimization engine for engineering design optimization problems [Текст] / Hsu Yeh-Liang, Liu Tzu-Chi // Engineering Optimization.Vol. 39, No. 6, September 2007, 679–700.
10. Металлические конструкции. В 3 т. Справочник проектировщика [Текст] / Под ред. В.В.Кузнецова. -М.: Изд-во АСВ, 1998. -576 с.