Деформированные мартингалы и их свойства

Аннотация

И.В. Павлов, О.В. Назарько

Дата поступления статьи: 30.10.2013

С помощью так называемых деформаций, представляющих собой семейства вероятностных мер на сигма-алгебрах, образующих фильтрацию, водится понятие деформированного мартингала, обобщающего классическое понятие мартингала с дискретным временем. Существенным образом различаются два типа таких деформированных мартингалов, названных авторами деформированными мартингалами 1-го и 2-го рода. Аналогично вводятся деформированные суб- и супермартингалы 1-го и 2-го рода. Доказано, что инфимум произвольного семейства деформированных супермартингалов есть деформированный супермартингал, а выпуклая функция от деформированного мартингала есть деформированный субмартингал. Кроме того, для деформированных мартингалов 2-го рода получено телескопическое свойство.

Ключевые слова: Фильтрация, вероятностная мера, деформация, деформированный мартингал, телескопическое свойство

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Настоящая работа посвящена изучению некоторых основополагающих свойств деформированных мартингалов 1-го и 2-го рода. Актуальность научного направления, в рамках которого выполнена работа, подробно обоснована во введении статьи [1], которая посвящена моделированию деформаций (см. также работы [2–3]). Приложения данной тематики продемонстрированы, например, в работах [4–5].
Пусть  — фильтрованное пространство с дискретным временем, где  — произвольное множество, а  — возрастающая последовательность -алгебр на нем (фильтрация). Для удобства мы введем также . Рассмотрим семейство  вероятностных мер , определенных на . Семейство Q называется деформацией 1-го рода (D1), если при всех  выполняется соотношение абсолютной непрерывности , и деформацией 2-го рода (D2), если выполняются обратные соотношения. Если выполняются и те, и другие соотношения, то деформация Q называется слабой (WD). 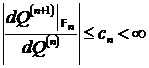D1 (соотв., D2) называется ограниченной — BD1 (соотв., BD2), если   -п.н. (соотв., 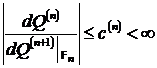 -п.н.). Основные свойства деформаций подробно изучены в [6].
Предположим, что при всех  случайные величины (с.в.)  интегрируемы по мере .
Определение 1. 1) Пусть Q – D1. Процесс  будем называть деформированным мартингалом первого рода (DM1), если  справедливо равенство

-п.н. (1)

2) Если Q есть D2, то процесс  будем называть деформированным мартингалом 2-го рода (DM2) при выполнении  равенства

-п.н. (2)

3) Предположим, что Q есть WD. Если процесс  является одновременно DM1 и DM2, то его будем называть слабо деформированным мартингалом (WDM).
Замечание 1. 1) Предположим, что  и  являются представителями условного матожидания в равенстве (1). Ясно, что , однако  может не равняться нулю. Поэтому некорректно требовать выполнение равенства (1) -п.н. Покажем корректность формулы (1). Если процесс  Q-неотличим от процесса , то для всех   -п.н. Известно, что  -п.н. Также  -п.н.   -п.н. Из всего этого вытекает, что  -п.н. Аналогичным образом обосновывается корректность формулы (2). Примеры деформированных мартингалов можно найти в [7].
Предложение 1. 1) Если  есть DM1, то

2) Если  есть DM2, то

Доказательство тривиально.
Определение 2.  Процесс  называется деформированным субмартингалом 1-го рода – DSubM1 (соотв., деформированным супермартингалом 1-го рода – DSupM1), если в формуле (1) знак “” поставить вместо знака “=” (соотв., знак “” поставить вместо знака “=”). По тому же принципу определяются деформированные субмартингалы и супермартингалы 2-го рода и слабо деформированные суб- и супермартингалы (DSubM2, DSupM2, SDSubM, SDSupM).
Предложение 2 (телескопическое свойство). Пусть Q есть D2 (соотв., BD2), а случайный процесс  таков, что   (соотв., ). Этот процесс является DM2 (соотв., DSubM2, DSupM2) если и только если  справедливо равенство

-п.н.

(соотв., равенство

-п.н.

и

-п.н.

Доказательство опускается.
Предложение 3. Пусть  – DSubM1 (соотв. DSubM2). Этот процесс является DM1 (соотв., DM2) в том и только в том случае, когда

(соотв.,

).

Доказательство опускается.
Предложение 4. Пусть  – некоторое семейство, состоящее из DSupM1 (соотв., DSupM2), где  — параметр. Определим , . Тогда процесс  есть DSupM1 (соотв., DSupM2).
Доказательство. Имеем :
.
Нетрудно проверить, что если деформация Q есть D1 (то есть речь идет о DSupM1), то записанные равенства и неравенства понимаются -п.н. Если же деформация Q есть D2 (то есть речь идет о DSupM2), то эту цепочку соотношений можно понимать -п.н., что и требовалось доказать.
Предложение 5. Если  есть деформированный мартингал 1-го или 2-го рода (соответственно, деформированный субмартингал 1-го или 2-го рода), а  – выпуклая (соответственно, выпуклая возрастающая) функция на , удовлетворяющая условию , , то процесс  – деформированный субмартингал того же рода, что и .
Доказательство. Обозначим . Если  – DM, то
.
Если  – DSubM, то  в силу монотонного возрастания функции . В обоих случаях . Применяя неравенство Йенсена, получаем :
.
Легко видеть, что если  – D1 и  – DM1 (соотв., DSubM1), то все записанные в этом доказательстве соотношения можно понимать -п.н. Если же  – D2 и  – DM2 (соотв., DSubM2), то все соотношения можно понимать -п.н. Доказательство закончено.
В заключение отметим, что классические варианты доказанных в данной работе результатов можно найти в [8-9]. Применение метода хааровских интерполяций к деформированным финансовым рынкам продемонстрировано в [10].
Данная работа выполнена при поддержке РФФИ, грант № 13-01-00637а.

Литература:

1. Назарько О.В., Павлов И.В. Рекуррентный метод построения слабых деформаций по процессу плотностей в рамках модели стохастического базиса, снабженного специальной хааровской фильтрацией [Текст] // Вестник РГУПС, 2012. – №1. – С. 200–208.
2. Назарько О.В.(B,S)-рынки на деформированных стохастических базисах [Текст] // Известия ВУЗов. Северо-Кавказский регион. Естественные науки, 2008. – Вып. 3. – С. 19–21.
3. Назарько О.В. Слабые деформации на бинарных финансовых рынках [Текст] // Известия ВУЗов. Северо-Кавказский регион. Естественные науки, 2010. – Вып. 1. – С. 12–18.
4. Назарько О.В., Павлов И.В., Чернов А.В. Моделирование оптимальной полосы пропускания телекоммуникационных каналов при условии гарантированной и негарантированной доставки пакетов [Электронный ресурс] // «Инженерный Вестник Дона», 2012, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2012/652 (доступ свободный). – Загл. с экрана. – Яз. рус.
5. Красий Н.П. О вычислении спрэда для обобщённой модели (B,S)-рынка в случае скупки акций [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1378 (доступ свободный). – Загл. с экрана. – Яз. рус.
6. Назарько О.В., Павлов И.В., Чернов А.В.Деформации и деформированные стохастические базисы [Текст]// В сб.: «Математические методы в современных и классических моделях экономики и естествознания: материалы региональной научно-практической конференции профессорско-преподавательского состава и молодых ученых РГЭУ (РИНХ)», 2012. – Ростов-на-Дону: Ростовский государственный экономический университет (РИНХ). – С. 37–53.
7. Назарько О.В., Павлов И.В. Два «классических» примера деформированных мартингалов 1-го рода [Текст] // Тезисы международной научно-практической конференции «Строительство 2012», 2012. – Ростов-на-Дону, РГСУ.
8. Neveu J. Discrete-Parameter Martingales [Текст] // North-Holland Pub. Company, Amsterdam, 1975. – 236 p.
9. Long R. Martingale Spaces and Inequalities [Текст] // Peking University Press, 1993. – 346 p.
10. Павлов И.В., Назарько О.В. Хааровские интерполяции финансовых рынков на деформированных стохастических базисах (Электронный ресурс) // Тезисы докладов международной научной конференции «Теория операторов, комплексный анализ и математическое моделирование», 2011. – ЮМИ ВНЦ РАН и РСО-А, Волгодонск. – С. 155-156.