Определение прогибов балок с гофрированной стенкой с учетом сдвиговых деформаций
Аннотация
Дата поступления статьи: 10.01.2013Настоящая статья посвящена вопросам аналитического определения прогибов балок с гофрированной стенкой. Получена зависимость для приведенного модуля сдвига, который необходимо учитывать при определении составляющей части прогиба от сдвиговых деформаций. С помощью энергетического метода в форме Ритца решена задача определения прогибов с учетом изгибных и сдвиговых деформаций. В качестве примера рассмотрена шарнирно опертая балка по двум сторонам постоянного и переменного сечения и даны окончательные зависимости при трех видах нагрузки. Представлены результаты расчета числовых примеров для трех основных очертаниях гофров стенки. Полученные числовые результаты с большой точностью согласуются с расчетами по методу конечных элементов.
Ключевые слова: балка, гофрированная стенка, энергия, работа, прогиб, сдвиг
Двутавровые балки с гофрированными стенками (БГС) активно применяют в современном строительстве. Согласно работам [1, 2] прогибы БГС реко¬мендуется вычислять с учетом изгибных и сдвиговых деформаций. Несмотря на широкое изучение БГС, расчетные зависимости для определения их прогибов окончательно не разработаны. Цель работы - разработать методику аналитического расчета прогибов двутавровых балок с гофрированной стенкой при действии поперечной нагрузки. В данной работе рассматриваются балки с различными очертаниями гофров при различных видах нагружения. Гофрированная балка представляется в виде трехслойной конструкции и считается, что пояса воспринимают равномерные нормальные напряжения, а стенка – равномерные напряжения сдвига по высоте сечения. Внешние слои (полки) плоские и такие тонкие по отношению к высоте поперечного сечения, что собственной жесткостью на изгиб можно пренебречь. Исходя из этих предположений, можно применить основные зависимости для многослойных конструкций, изложенные в [3]. Проверка точности решения производится численными расчетами методом конечных элементов (МКЭ). Для определения прогибов гофрированная стенка заменяется на плоскую ортотропную пластинку такой же толщины. При этом необходимо определить упругие постоянные, которые зависят от вида и размеров гофра и определяются путем сравнения деформации гофрированной и плоской ортотропной пластинки при одних и тех же нагрузках. Для расчета прогибов с учетом сдвига достаточно определить только модуль сдвига в вертикальном направлении (вдоль гофров).
|
|
|
|
а |
б |
|
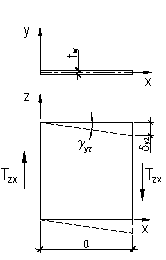
Рис. 1. – К определению приведенного модуля сдвига G*
а – сдвиг гофрированной стенки; б – сдвиг плоской ортотропной стенки |
|
оставляющая часть прогиба от сдвиговых деформаций для гофрированной стенки будет равна (рис. 1)
 (1)
(1)
где α – коэффициент, зависящий от распределения касательных напряжений по сечению; Tzx – сдвигающая сила; G – модуль сдвига изотропного тела; s – длина дуги или панели полуволны; Aw – площадь поперечного сечения стенки.
Составляющая часть прогиба для стенки, выполненной из плоского ортотропного листа, равна
![]() (2)
(2)
где G* – приведенный модуль сдвига стенки; а – длина пластинки (длина полуволны).
Приравнивая (1) и (2), определим приведенный модуль сдвига стенки в вертикальном направлении:
![]() (3)
(3)
|
|
|
|
|
Волнистый
s = a·k
где {C}{C}{C}{C}{C}{C} |
Треугольный
s = a1
{C}{C}{C}{C}{C}{C} |
Трапецеидальный
s = a1 + a3
|
|
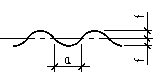
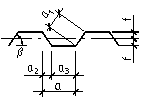
Рис. 2. – Профиль гофрированной стенки |
||
Приведенный модуль сдвига определяется для трех основных очертаний гофрированных стенок, применяемых для балок в современной практике: волнистый, треугольный, трапецеидальный (рис. 2).
|
|
|
|
а |
б |
|
Рис. 3. – К расчету прогибов балки:
а – размеры поперечного сечения; б – деформированный элемент трехслойной балки |
|
На основании предпосылки о малой толщине полок можно допустить, что продольные перемещения всех точек по толщине полки одинаковые и их можно заменить значениями перемещения соответствующего центра тяжести полки, тогда (рис. 3б)
![]() (4)
(4)
где af1 и af2 – расстояния от центра тяжести полок до центра тяжести балки;
γ1 - угол сдвига стенки от действия поперечных сил, равный
![]() (5)
(5)
где γ – угол поворота сечения стенки;
![]() – угол поворота поперечного сечения от действия изгибающих моментов;
– угол поворота поперечного сечения от действия изгибающих моментов;
ω – общий прогиб балки
Деформации нижнего и верхнего пояса с подстановкой (4) составляют:
![]() (6)
(6)
Закон Гука для деформации стенки при сдвиге выглядит следующим образом:
![]() ,
,
где γk – полный угол сдвига стенки.
Между углами сдвига γ и γk существует зависимость (рис. 3б): {C}{C}{C}{C}{C}{C}![]() ,
,
где hf = hw + 0.5·tf1 + 0.5·tf2 – расстояние между центрами тяжести полок.
hw – высота стенки.
Ввиду малой толщины полок можно принять hf = hw, тогда γk = γ, а напряжения будут
![]() . (7)
. (7)
Закон Гука для деформации внешних слоев при продольном растяжении имеет вид:
![]() (8)
(8)
где E – модуль упругости нижней и верхней полки соответственно.
При определении прогибов чаще всего прибегают к использованию приближенных методов, к которым относится энергетический метод. Энергия деформации U изогнутой многослойной балки длиной L с тонкими внешними слоями получается из формулы:
![]() (9)
(9)
Подставив в уравнение (9) напряжения и деформации согласно (5)-(9) и выполнив интегрирование по ширине и высоте балки и с учетом переменных по длине значений поперечного сечения, получим
![]() (10)
(10)
где If(x) – момент инерции полок относительно оси центра тяжести сечения;
Aw(x) – площадь стенки.
Внешняя нагрузка многослойной балки состоит из поперечной нагрузки q(х) и вертикальной сосредоточенной силы P. Работа внешних сил равна
![]() (11)
(11)
Поперечная нагрузка и сосредоточенная сила считаются положительными, если их направление совпадает с направлением оси z, а значит {C}{C}{C}{C}{C}{C}![]() {C}{C}{C}{C}{C}{C}; {C}{C}{C}{C}{C}{C}
{C}{C}{C}{C}{C}{C}; {C}{C}{C}{C}{C}{C}![]() .
.
Тогда работа внешних сил (11) выглядит следующим образом:
![]() (12)
(12)
Полная энергия деформаций определяется по формуле:
Э = U - T (13)
Полная энергия деформации (13) является функционалом. Условие достижения экстремума (минимума) полной энергии деформаций имеет вид:
dЭ = dU - dT = 0, (14)
где d - знак вариации функционала.
В случае решение задачи методом Ритца ω(x) и γ(x) могут быть записаны в форме:
![]() (15)
(15)
где ωj(x), γj(x) (j = 1,2,..., n) – произвольные функции, удовлетворяющие кинематическим граничным условиям опирания балки;
aj, bj - неопределенные коэффициенты.
Неопределенные коэффициенты aj, bj определяются из условий минимума функционала полной энергии деформаций (14). Условиями экстремума функции многих переменных являются условия равенства нулю первых производных по всем аргументам:
![]() (16)
(16)
Условия (16) дают бесконечную систему алгебраических уравнений, из решения которой определяются коэффициенты aj, bj. Если получить решение системы с произвольным числом членов ряда, то на основе метода Ритца можно получить точное решение задачи.
Для применения метода Ритца рассмотрим шарнирно опертую балку по двум сторонам.
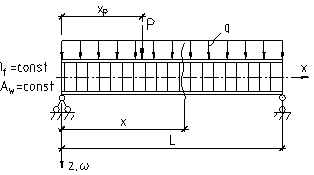
Пример 1. Балка находится под действие постоянной равномерно распределенной нагрузке q (x) = q. Значения поперечного сечения If и Aw постоянны (рис. 4 а). Граничные условия {C}{C}{C}{C}{C}{C}![]() .
.
В качестве сравнительных функций подходят тригонометрические функции:
![]() ,
, ![]() .
.
|
|
|
|
а |
б |
|
Рис. 4. – Расчетные схемы БГС а – постоянного сечения; б – переменного сечения |
|
Принимая один член ряда j=1 и дифференцируя принятые функции, получим:
![]()
Внося значения ![]() ,
, ![]() ,
, ![]() ,
, ![]() в равенства (10) и (12) и, используя (13), находим полную энергию деформации:
в равенства (10) и (12) и, используя (13), находим полную энергию деформации:
{C}{C}{C}{C}{C}{C}![]()
где ![]() - момент инерции полок балки;
- момент инерции полок балки;
Af1 = bf1·tf1, Af2 = bf2·tf2 – площадь нежней и верхней полки соответственно;
Aw = hw·tw - площадь стенки.
Дифференцируя полную энергию по a1 и b1, получаем систему, из которой находим коэффициенты:
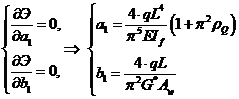
где ![]() .
.
Подставляя коэффициенты и принятые сравнительные функции в уравнения (15), получаем функции прогиба и угол поворота сечения стенки БГС. Для расчетов удобно перейти к безразмерным координатам, приняв ξ = x/L, тогда функция прогиба балки будет
![]() (17)
(17)
Пример 2. Рассмотрим балку под действием сосредоточенной силы P, расположенной на расстоянии xp. Значения поперечного сечения If и Aw постоянны (рис. 4 а). Если принять безразмерную координату точки приложения силы ε = xp/L, получим общий прогиб балки в произвольном сечении равный
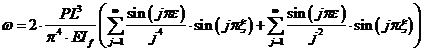 , где j = 1,3,5,7 … (18)
, где j = 1,3,5,7 … (18)
В упрощенном виде прогиб (18) можно представить как
![]() , (19)
, (19)
где α и β – параметры, зависящие от количества членов ряда, места расположения силы и сечения на балке:
- при j = 7; сила P в середине пролета - ε = 0,5; прогиб в ξ = 0,5: α = 1,02, β = 1,2.
- при j = 7; сила P в 1/3 пролета - ε = 1/3; прогиб в ξ = 0,5: α = 0,87, β = 0,8.
Прогибы от действия нескольких сил можно определить путем суммирования прогибов от каждой силы по формуле (18) на основе принципе независимости действия сил.
С целью проверки применимости полученных выше выражений (17) и (19) для оценки деформаций шарнирно опертых БГС были выполнены две серии расчетов.
В первой серии рассчитывалась балки при действии двух сосредоточенных сила P = 65 кН, действующих на расстоянии l/3 от каждой из опор. Длина полуволны и высота гофра, а также ширина и толщина полок всех балок приняты одинаковыми. Балки различались только профилем стенки (рис. 2). Все размеры балок и результаты расчета приняты из [4]: длина балки L = 6 м; сечение балки: hw = 500 мм; tw = 2,5 мм; bf1 = bf2 = 200 мм; tf1 = tf2 = 6 мм; a = 77,5 мм; f = 20 мм; гибкость стенки балок равняется λw = hw/tw = 200.
Модуль упругости стали E = 2,06·105 МПа, модуль сдвига G< = 0,8·105 МПа.
Для проверки надежности полученных результатов по (17) и (19) были выполнены расчеты этих же балок методом конечных элементов в программном комплексе «Лира». Моделирование балок и принятая сетка конечных элементов описано в [4]. Результаты расчета МКЭ приведены в табл. 1.
Таблица №1
Результаты расчета балок постоянного сечения с одинаковой гибкостью
|
Вид профиля стенки |
Пролет L, м |
Нагрузка |
Прогиб в середине пролета (ξ=0,5), ω, мм |
δ % |
||||
|
Метод Ритца |
МКЭ ω2 |
|||||||
|
ωM |
ωQ |
ωQ·100%/ ωM |
ω1 |
|||||
|
Волнистый |
6 |
2P |
15,92 |
1,48 |
9,3 |
17,4 |
17,52 |
0,7 |
|
Треугольный |
15,92 |
1,43 |
9,0 |
17,35 |
17,32 |
0,2 |
||
|
Трапецеидальный |
15,92 |
1,54 |
9,7 |
17,46 |
17,86 |
2,2 |
||
Сравнительный анализ показывает удовлетворительное соответствие результатов расчета по предложенной методике и МКЭ. Расчет по предлагаемой методике дает расхождение в прогибах не выше 2,2% при использовании (19). Из табл. 1 видно, что составляющая часть прогиба от сдвиговых деформаций зависит от профиля стенки при одинаковых параметрах сечения. Расчеты по предложенной методике показывают, что БГС с гофром треугольного очертания имеет лучшую изгибную жесткость, это же и видно из расчета МКЭ. Хотя разница в прогибах между балками очень мала (1%).
Таблица №2
Параметры гофрированных балок (рис. 2, 3а)
|
№ п.п |
Пролет L, м |
hw, мм |
tw, мм |
λw = =hw/tw |
bf1= bf2, мм |
tf1= tf2, мм |
a, мм |
f, мм |
a1, мм |
a2, мм |
a3, мм |
|
1 |
9 |
750 |
2.5 |
300 |
200 |
12 |
77.5 |
20 |
- |
- |
- |
|
2 |
6 |
500 |
6 |
83 |
200 |
10 |
150 |
40 |
170 |
- |
- |
|
3 |
6 |
500 |
5 |
100 |
220 |
10 |
240 |
20 |
56,57 |
40 |
200 |
Во второй серии рассчитывались балки при двух видах нагружения: равномерно распределенной нагрузкой интенсивностью q=100 кН/м; одной сосредоточенной силой P = 120 кН, приложенной в середине пролета. Также проводилась оценка влияния гибкости стенки λw на общий прогиб балки (табл. 2). Это связано с тем, что при небольшой гибкости стенки участки, примыкающие к полкам, начинают воспринимать нормальные напряжения и их надо учитывать при определении геометрических характеристик. Результаты расчета МКЭ приведены в табл. 3
Таблица №3
Результаты расчета балок постоянного сечения с различной гибкостью
|
Вид профиля стенки |
Пролет L, м |
Нагрузка |
Прогиб в середине пролета (ξ=0,5), ω, мм |
δ % |
||||
|
Метод Ритца |
МКЭ ω2 |
|||||||
|
ωM |
ωQ |
ωQ·100%/ ωM |
ω1 |
|||||
|
Волнистый |
9 |
q |
59,52 |
8,08 |
13,6 |
67,6 |
69,17 |
2,3 |
|
P |
12,82 |
2,05 |
16,0 |
14,87 |
14,99 |
0,8 |
||
|
Треугольный |
6 |
q |
31,5 |
2,19 |
7,0 |
33,69 |
33,96 |
0,8 |
|
P |
10,17 |
0,83 |
8,2 |
11,0 |
11,01 |
0,1 |
||
|
Трапецеидальный |
6 |
q |
28,63 |
2,47 |
8,6 |
31,1 |
31,04 |
0,2 |
|
P |
9,25 |
0,94 |
10,2 |
10,19 |
10,07 |
1,2 |
||
Из табл. 3 видно, что при гибкости стенки λw=83 не наблюдается серьезной погрешности при определении прогибов балок. Расчет по предлагаемой методике дает расхождение в прогибах не выше 2,3% при использовании зависимостей (17) и (19).
Прогибы от сдвиговых деформаций для представленных балок (табл. 1, 3) составляют 6-16% от изгибных деформаций. С целью определения влияния сдвиговых деформаций было рассчитано 20 балок с разными параметрами. Анализ данных показал, что сдвиговые деформации могут составлять 3-50% от изгибных деформаций.
Наряду с расчетом БГС постоянного сечения предложенную методику, основанную на методе Ритца, удобно применять и для балок, у которых значения поперечного сечения If и Aw являются постоянными лишь по участкам или переменными по длине участка.
Пример 3. Рассмотри балку переменного сечения. Балка находится под действие постоянной равномерно распределенной нагрузке q (x) = q. Высота поперечного сечения балки изменяется по длине балки (рис. 4 б). Характеристики поперечного сечения If и Aw изменяются по следующим законам:
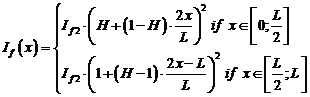 ;
;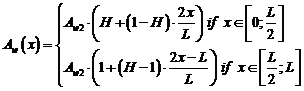
где ![]() ;
; ![]() ;
; ![]() ;
;
hf1, hf2 - расстояние между центрами полок на опоре и в пролете соответственно;
hw2 – высота стенки балки в пролете.
Полная энергия деформации с учетом двух участков определяется по формуле
![]() Для определения функции прогибов балки проводим математические действия аналогично примеру 1. После расчета получаем
Для определения функции прогибов балки проводим математические действия аналогично примеру 1. После расчета получаем
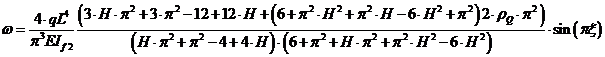
Вычисления целесообразно проводить на ЭВМ, например, с помощью с математического пакета Mathcad.
Таблица № 4
Параметры БГС переменного сечения и результаты расчета при q = 100 кН/м (рис. 2, 4б)
|
Пролет L, м |
Вид профиля стенки |
hw1, мм |
hw2, мм |
tw, мм |
bf1= bf2, мм |
tf1= tf2, мм |
a, мм |
f, мм |
Прогиб в середине пролета (ξ=0,5), ω, мм |
δ % |
|
|
Метод Ритца |
МКЭ |
||||||||||
|
6 |
Волнистый |
300 |
500 |
3 |
200 |
10 |
77,5 |
20 |
46,4 |
46,04 |
0,8 |
Разница в прогибах при расчете балки переменного сечения составляет 0,8%.
Выводы.
- предложенная методика, основанная на методе Ритца, для определения прогибов БГС постоянного и переменного сечения с различной гибкостью стенок дает хорошие результаты, подтверждаемые расчетами МКЭ;
- прогибы от сдвиговых деформаций могут составлять 3-50% от изгибных деформаций и зависят от длины балки и от параметров поперечного сечения;
- прогибы БГС во всех случаях необходимо определять с учетом изгибных и сдвиговых деформаций;
- при определении составляющей части прогиба от сдвиговых деформаций необходимо применять приведенный модуль сдвига (3).
Литература
1. Бирюлев, В.В. Проектирование металлических конструкций: Специальный курс [Текст] / В.В. Бирюлев, И.И. Кошин, И.И. Крылов, А.В. Сильвестров, под ред. В.В. Бирюлева. – Л.: Стройиздат, 1990. – 432 с.