Оптимальное управление порожними вагонами различных форм собственности

Аннотация

К. Р. Рахимов

  Полувагоны, как известно, являются универсальным подвижным составом. На сегодняшний день в РЖД и в транспортных ВУЗах страны активно ведутся работы научно-исследовательского характера по оптимизации регулирования и эксплуатации универсальным подвижным составом. В статье поставлена задача по оптимальному управлению порожными вагонами различных форм собственности с использованием транспортной задачи.

Ключевые слова: Парк полувагонов, вагоны собственные привлеченные (ВСП), порожный вагонопоток, Первая грузовая компания (ПГК), Вторая грузовая компания (ВГК), базисный план

05.22.08 - Управление процессами перевозок

Введение
Для Российских железных дорог, парк универсальных вагонов является важным сегментом, ведь на полувагоны приходится более 50% сетевой погрузки и почти две трети (57%) грузооборота. При этом универсальный парк растет наиболее динамичными темпами: за последние пять лет он увеличился почти в 1,5 раза и достиг 480 тыс. ед. В то же время погрузка в полувагоны в 2011 году была на 11% ниже, чем в 2006-м (31 тыс. ед. в сутки), что свидетельствует о снижении эффективности использования вагонного парка в условиях изменения формы собственности. Еще один факт: доля порожнего пробега полувагонов увеличилась с 27% в 1988 году до более чем 40% в 2011-м. Это вызвано нерациональными перевозками порожних вагонов, принадлежащих множеству собственников и операторов, значительно увеличившими нагрузку на инфраструктуру [1].
В 20 декабря 2011 года Правительством РФ было принято постановление №1051, которое установило порядок привлечения в аренду универсальных полувагонов ОАО «Вторая грузовая компания» и других собственников подвижного состава под управление единого перевозчика РЖД.
Во исполнение правительственного постановления в течении февраля-марта 2012 года на базе ресурсов ОАО «ВГК» был сформирован парк ВСП (вагоны собственные привлеченные). Между РЖД и ВГК подписан договор, регулирующий порядок и условия привлечения перевозчиком 107 тыс. полувагонов своей дочерней компании.

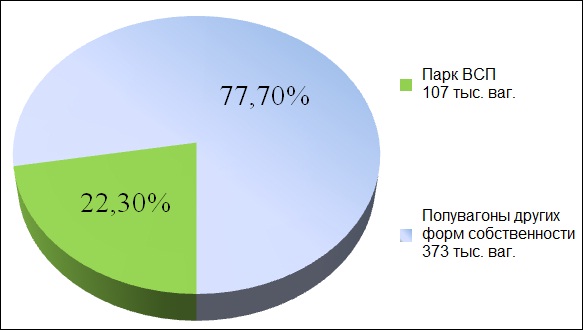
Рис. 1. Соотношение парка полувагонов ВСП к общему парку полувагонов в процентом исчислении.

Как известно, управление привлеченными полувагонами осуществляется на принципах обезличенности, что позволяет снизить влияние таких негативных факторов, как длительные простои порожнего приватного подвижного состава в ожидании наиболее выгодных перевозок, массовое встречное перемещение однотипного порожняка, принадлежащего разным собственникам, увеличение сортировочной работы и т.д.[2].

Постановка задачи
Поскольку управление порожними вагонами является транспортной задачей, рассмотрим задачу, где участвуют вагоны различных форм собственности.
Пусть в пунктах A₁,A₂, ...,A_m находятся порожние вагоны, причем в пункте A_i находится, соответственно, a_i вагонов под управлением перевозчика (вагоны парка ВСП) и a*_i вагонов других форм собственности (фирм, иностранных и т. д.).
Эти вагоны должны быть поданы под погрузку в пункты B₁,B₂, …, B_n, причем заявки этих пунктов составляют, соответственно, b₁,b₂, ..., b_n вагонов. В общем случае исходными данными являются:
Удобно задачу представить в табличном виде:
Таблица 1

Задача, отображающая таблицу, не является классической транспортной задачей и не может быть решена методами решения транспортных задач из-за наличия в пунктах отправления принципиально разных  вагонов с точки зрения затрат на перемещение этих вагонов в пункты назначения. Однако, эта задача может быть преобразована в другую, которая уже будет классической транспортной задачей.
Идея преобразования состоит в том, чтобы реальным пунктам A₁, A₂, ..., A_m поставить в соответствие эти пункты, но с запасами a₁,a₂,…,a_m и, якобы другие, но по существу те же пункты с другими индексами A_m+1, A_m+2, …, A_m+m с запасами a₁*,a₂*,…,a_m* и соответствующими стоимостями перемещений вагонов. Тогда вышеприведенная таблица преобразуется в таблицу
Таблица 2

Задача, соответствующая этой таблице, уже может быть решена методами решения транспортной задачи.
Пример
Решить задачу оптимального управления порожними вагонами, заданную следующей таблицей
Таблица 3

В соответствии с предложенным выше алгоритмом для вагонов других форм собственности из пункта A₁ вводим фиктивный пункт A₃, а для соответствующих вагонов из пункта A₂ – фиктивный пункт A₄. Кроме того, так как суммарное число заявок (140) меньше суммарного числа запасов (160), то для приведения задачи к классической транспортной задаче вводим фиктивный пункт назначения B₄ с заявкой 20 (160-140=20) и с нулевыми стоимостями перевозок. Тогда задача преобразуется в задачу, представленную таблицей
Таблица 4.

Эта задача является классической сбалансированной транспортной задачей, и она может быть решена методами решения этой задачи.
Начальный базисный план будем получать по методу наименьшей стоимости по строчкам. Этот план представлен нижеприведенной таблицей 5.
Значение критерия (стоимость перевозок) для этого базисного плана будет равно:
f(X_б)=80×35+110×05+90×20+100×45+260×30+220×05+00×20=18550.
Чтобы улучшить этот базисный план или убедиться, что план оптимальный, применим метод потенциалов. Выберем для пунктов отправления A_i потенциалы - u_i, а для пунктов назначения B_j, соответственно, потенциалы v_j. Составим систему уравнений для потенциалов, основываясь на базисных клетках таблицы 5:
v₂ – u₁ = 80, v₁ – u₂ = 110, v₂ – u₂ = 90, v₃ – u₂ =100,
v₁ – u₃ =260, v₁ – u₄ = 220, v₄ – u₄ = 0.

Таблица 5

Полагая u₁ = 0, для остальных значений потенциалов из этой системы получим: v₂ = 80, v₁ = 100, u₂ = - 10, v₃ = 90, u₃ = - 160, u₄ = - 120, v₄ = - 120. Вычислим теперь значения  псевдостоимостей  Ĉ_ij= v_j– u_i  для свободных клеток: Ĉ₁₁ = 100, Ĉ₁₃ = 90, Ĉ₁₄ = - 120, Ĉ₂₄ = - 110, Ĉ₃₂ = 240, Ĉ₃₃ = 250, Ĉ₃₄ = 40, Ĉ₄₂ = 200, Ĉ₄₃ = 210, Ĉ₄₄ = 0. Для всех свободных клеток, кроме трех, выполняются неравенства Ĉ_ij≤C_ij. Для клеток (3,2), (3,3) и (3,4) имеет место противоположный знак. На основе клетки (3,2) осуществим циклическое перемещение перевозок с целью получения лучшего базисного плана. Переместим 20 единиц груза (20 вагонов) из базисной клетки (2,2) в свободную клетку (3,2), затем для соблюдения баланса из 30 вагонов клетки (3,1) 20 вагонов переместим в клетку (2,1). Цикл замкнулся. Новый базисный план, соответствующий этим перемещениям в таблице, представлен в новой таблице:

Таблица 6

Значение критерия для этого базисного плана равно:
f(X_б) = 80×35+110×25+100×45+260×10+190×20+220×05+00×20 = 17550.
Как видно из значения критерия полученный базисный план лучше предыдущего плана. Проделав еще несколько итераций в методе потенциалов, получим базисный план, соответствующий таблице:
Таблица 7

Составляя систему уравнений для потенциалов базисных клеток этой таблицы, получим:
v₂ – u₁= 80, v₃ – u₁ =90, v₃ – u₂ = 100, v₁ – u₂ = 110,
v₂ – u₃ = 190, v₁ – u₄ =220, v₄ – u₄ = 00.
Решая эту систему, для потенциалов получим следующие значения:
u₁ = 0, v₂ = 80, v₃ =90, v₁ = 100, u₂ = -10,
u₃ = -110, u₄ = - 120, v₄ = -120.
Отсюда для псевдостоимостей свободных клеток получим:
Ĉ₁₁ = 100, Ĉ₁₄ = - 120, Ĉ₂₂ = 90, Ĉ₂₄ = - 110,Ĉ₃₁ = 220,
Ĉ₃₃ = 200, Ĉ₃₄ = -10, Ĉ₄₂ = 200,Ĉ₄₃ = 210.
Нетрудно убедиться, что для  всех клеток выполняются условия, Ĉ_ij≤С_ij, а это означает, что полученный базисный план является оптимальным. Итак, 40 вагонов, необходимых для пункта B₁, доставляются в этот пункт следующим образом – 35 вагонов перевозчика из пункта A₂ и 5вагонов других форм собственности из этого же пункта; соответственно, 55 вагонов для B₂ доставляются – 25 вагонов перевозчика из пункта A₁ и 30вагонов других форм собственности из этого же пункта; аналогично, 45 вагонов для B₃ доставляются – 10 вагонов перевозчика из пункта A₁ и 35 вагонов перевозчика из пункта A₂. В фиктивный пункт назначения из-за нулевой стоимости перевозок ничего не направляется, 20 вагонов других форм собственности остаются в пункте A₂.

Заключение
Классические методы решения транспортных задач используются довольно с долгих времен, и считаются самыми эффективными. И в нынешних условиях применения таких методов, безусловно, принесут положительные результаты в организации порожних вагонопотоков.

Литература

1.Управление парками: адаптация к современным условиям. Интервью с вице-президентом ОАО «РЖД» Анатолием Краснощеком. РЖД-Партнер №9 (229) май 2012. С 66-69.
2.Нам требуется гибкая политика. Интервью с первым вице-президентом ОАО «РЖД» Вадимом Морозовым. РЖД-Партнер №7 (227) апрель 2012. С 16-19.