Программная реализация трехмерной математической модели транспорта взвеси в мелководных акваториях

Аннотация

Е.Е. Дегтярева, Е.А. Проценко, А.Е. Чистяков

Работа посвящена моделированию транспорта взвесей в мелководных акваториях. Результаты математического и численного моделирования могут быть применены на практике для обоснования проектирования и строительства гидротехнических сооружений, для прогноза формирования рельефа дна (в частности прогнозирования транспорта взвесей), для решения проблем, связанных с защитой от заносимости портов и каналов, прогнозом силового воздействия на конструкции, для определения оптимальных трасс морских подходных каналов и т.п.

Ключевые слова: математическое моделирование, гидродинамика, транспорт веществ, уравнение Навье-Стокса, уравнение диффузии-конвекции-реакции

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Целью работы является моделирование механизмов формирования поля концентрации взвесей и его пространственно–временной изменчивости на основе натурных данных и численного моделирования; построение и исследование математических моделей, способных адекватно описывать процессы подъема, переноса и осаждения, а также построение эффективных алгоритмов для описания изменения концентрации взвесей и транспорта наносов; реализация эффективных численных методов и алгоритмов в виде проблемно-ориентированного программного комплекса для проведения вычислительного эксперимента.
Исходными уравнениями модели являются:
- уравнение движения водной среды[1-3]:

- уравнение транспорта взвешенных частиц[4-6]:

- уравнение транспорта наносов[7-8]:
           
где
Здесь  - концентрация взвешенных частиц,  - скорость движения водной среды, - скорость осаждения,  - глубина водоема,  - напряжение на дне,  - критическое напряжение,  - коэффициент турбулентного обмена,  - плотность водной среды,  - давление,  - пористость грунта,  - экспериментальные коэффициенты,  - внешняя сила,  - критический угол при котором начинается транспорт наносов,  – функция Хэвисайда,  - функция, описывающая распределение и мощность источников примесей.
Для аппроксимации модели движения водной среды по временной переменной использовался метод поправки к давлению, применены аддитивные двумерно – одномерные разностные схемы, устойчивость которых исследовалась на основе сеточного принципа максимума. Исходная непрерывная задача была преобразована в систему линейных алгебраических уравнений, которая была решена при помощи построенного проблемно - ориентированного программного комплекса. Для решения сеточных уравнений использован адаптивный попеременно-треугольный итерационный метод [9-10]. На рис. 1представлены результаты численного моделирования распределения концентрации взвешенного вещества на расчетном интервале 24 ч и 150ч.

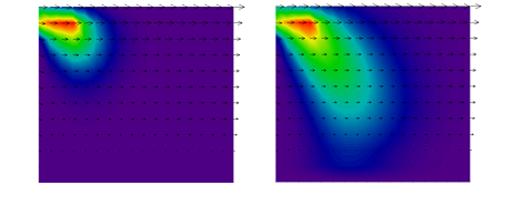
Рис.1 - Значение концентрации взвешенного вещества в центральной части расчетной области на расчетном интервале через 24 ч и 150ч

На рис. 3 представлены значения глубины в расчетном интервале 100 ч.

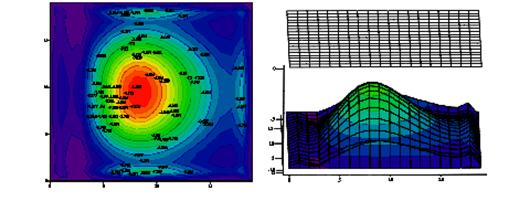
Рис. 2- Значение глубины в расчетном интервале 100 ч

 Результаты эксперимента позволяют проанализировать динамику изменения геометрии дна, функции возвышения уровня, образования структур и наносов. Данная математическая модель и разработанный комплекс программ позволяют предсказать динамику изменения рельефа дна, появление морских гряд и кос, их рост и трансформацию, а также прогнозировать изменение поля концентрации в случае выброса от источника.
Выводы. Разработана трехмерная математическая модель для расчета транспорта взвешенного материала применительно к мелководным акваториям, которая в отличие от известных моделей учитывает наиболее полно процессы диффузии-конвекции, подъема, переноса и осаждения взвеси, транспорта наносов, движения водной среды, с учетом турбулентного обмена по вертикальному направлению, а также сложную геометрию дна и береговой линии.
На основе построенных математических моделей и адаптированных к объединенной дискретной модели гидродинамики и транспорта взвесей численных алгоритмов разработан и реализован комплекс программ, обладающий проблемно-ориентированным интерфейсом и средствами визуализации для численного решения задач транспорта взвешенного материала на языке  С++  и проведены на его основе численные эксперименты, результаты которых согласуются с реальными физическими процессами.

Литература

1. Алексеенко Е.В., Сидоренко Б.В., Колгунова О.В., Чистяков А.Е. Сравнительный анализ классических и неклассичнских моделей гидродинамики водоемов с турбулентным обменом// Известия ЮФУ. Технические науки. –2009. №8 (97). – С 6-18.
2. Сухинов А.И., Чистяков А.Е. Параллельная реализация трехмерной модели гидродинамики мелководных водоемов на супервычислительной системе// Вычислительные методы и программирование: Новые вычислительные технологии. – 2012. – Т.13, №1  – С. 290–297.
3. Сухинов А.И., Чистяков А.Е., Тимофеева Е.Ф., Шишеня А.В. Математическая модель расчета прибрежных волновых процессов// Математическое моделирование. – 2012. – Т.24, №8, – С. 32–44.
4. Дегтярева Е.Е., Чистяков А.Е. Моделирование транспорта наносов по данным экспериментальных исследований в Азовском море// Известия ЮФУ. Технические науки. –2012. №2 (127). – С 112-118.
5. Сухинов А.И., Дегтярева Е.Е., Чистяков А.Е. Математическое моделирование транспорта донных отложений с учетом гидродинамических процессов// Известия ЮФУ. Технические науки. –2012. №6 (131). – С 57-62.
6. Чистяков А.Е. Трехмерная модель движения водной среды в Азовском море с учетом транспорта солей и тепла// Известия ЮФУ. Технические науки –2009. №8 (97). – С 75-82.
7. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Построение дискретной двумерной математической модели транспорта наносов// Известия ЮФУ. Технические науки. – 2011. №8 (121). – С 32-44.
8. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Двумерная гидродинамическая модель, учитывающая динамическое перестроение геометрии дна мелководных водоемов// Известия ЮФУ. Технические науки. –2011. №8(121). – С 159-167.
9. Сухинов А.И., Чистяков А.Е. Адаптивный модифицированный попеременно-треугольный итерационный метод для решения сеточных уравнений с несамосопряженным оператором// Математическое моделирование. – 2012. – Т.24, №1, – С. 3–20.
10. Никитина А.В., Чистяков А.Е., Н.А.Фоменко Н.А. Применение адаптивного модифицированного попеременно–треугольного итерационного метода для численной реализации двумерной математической модели движения водной среды// Инженерный вестник Дона. – 2012, – Т.20,  №2, – С. 335–339.