К вопросам построения интегральных операторов с осциллирующими коэффициентами в пространстве L2(Bn)
Аннотация
Дата поступления статьи: 30.10.2013Статья посвящена многомерным интегральным операторам с однородными ядрами и осциллирующими коэффициентами специального вида. Изучаются операторы, представляющие собой сумму слагаемых: канонический интегральный оператор с однородным ядром, оператор с осциллирующим коэффициентом и однородным ядром. Для данных операторов определено понятие символа, в терминах которого получен критерий нетеровности и формула вычисления индекса. Решение поставленной задачи основано на редукции многомерного интегрального уравнения к бесконечной диагональной системе одномерных уравнений.
Ключевые слова: Интегральные операторы с однородными ядрами, интегральные операторы с осциллирующими коэффициентами, критереий нетеровости, многомерные интегральные уравнения
05.13.18 - Математическое моделирование, численные методы и комплексы программ
В настоящее время имеется немало работ, посвященных многомерным интегральным операторам c однородными степени (-n) ядрами (см., например, [1-4], [7-8]). Для таких операторов получены необходимые и достаточные условия нетеровости и обратимости, описаны банаховы алгебры, порожденные этими операторами, найдены критерии применимости проекционного метода, интегральные операторы с однородными ядрами и переменными коэффициентами ([2], [3]). В данной статье рассматриваются операторы с радикальными осциллирующими коэффициентами вида![]() . Подчеркнем, что операторы с однородными ядрами и радикальными (по крайней мере в окрестности точки x=0) коэффициентами находят применение в некоторых задачах математической физики. В работе используются следующие обозначения:
. Подчеркнем, что операторы с однородными ядрами и радикальными (по крайней мере в окрестности точки x=0) коэффициентами находят применение в некоторых задачах математической физики. В работе используются следующие обозначения:![]()
![]() ;
;  -площадь сферы
-площадь сферы![]() ;
;![]()
В пространстве ![]() рассмотрим оператор (1)
рассмотрим оператор (1)
![]() ,
, ![]() где
где ![]() , а функция
, а функция ![]() удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) однородность степени (-n), то есть![]() ;
;
2) инвариантность относительно группы вращений![]() , то есть
, то есть ![]() ;
;
3) суммируемость, то есть 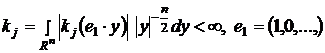
Рассмотрим в ![]() интегральный оператор (2) ,
интегральный оператор (2) ,![]() ,
,![]() ядро которого удовлетворяет условию (1).
ядро которого удовлетворяет условию (1).
Оператору ![]() сопоставим оператор
сопоставим оператор![]() , который определим формулой
, который определим формулой ![]() , (3)
, (3)
где ![]() - оператор вида (2) с ядром
- оператор вида (2) с ядром ![]() . Здесь и ниже мы отожествляем функции
. Здесь и ниже мы отожествляем функции ![]() и
и ![]() с операторами умножения на эти функции. Рассмотрим разность
с операторами умножения на эти функции. Рассмотрим разность![]() . Имеем
. Имеем ![]() . Так как
. Так как ![]() , то оператор
, то оператор![]() является компактным в
является компактным в![]() Следовательно, T-компактный оператор. Поскольку
Следовательно, T-компактный оператор. Поскольку ![]() , то оператор
, то оператор ![]() нетёров тогда и только тогда, когда нетёров оператор
нетёров тогда и только тогда, когда нетёров оператор![]() , причем
, причем ![]() .
.
Приступим к исследованию оператора![]() . В пространстве
. В пространстве ![]() рассмотрим уравнение, порожденное этим оператором:
рассмотрим уравнение, порожденное этим оператором:
![]() . (4)
. (4)
Поскольку функции ![]() удовлетворяют условию (2), то существуют такие функции
удовлетворяют условию (2), то существуют такие функции![]() , что
, что ![]() . Учитывая это, и переходя в последнем соотношении к сферическим координатам
. Учитывая это, и переходя в последнем соотношении к сферическим координатам![]() , получим
, получим
 (5) ,
(5) ,
![]() (6)
(6) ![]()
Функция ![]() удовлетворяет следующему условию суммируемости
удовлетворяет следующему условию суммируемости
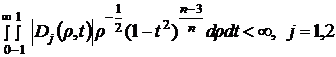 (7)
(7)
Умножая обе части уравнения (5) на сферические гармоники![]() , интегрируя по единой сфере, и применяя формулу Функа-Гекке, получим следующую бесконечную диагональную систему одномерных интегральных уравнений (8)
, интегрируя по единой сфере, и применяя формулу Функа-Гекке, получим следующую бесконечную диагональную систему одномерных интегральных уравнений (8)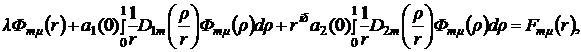
где![]() , а
, а ![]() - размерность пространства сферических гармоник порядка m.
- размерность пространства сферических гармоник порядка m.
![]()
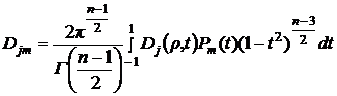 (9),
(9),
при этом ![]() - многочлены Лежандра.
- многочлены Лежандра.
В пространстве ![]() рассмотрим оператор
рассмотрим оператор![]() , формирующий левую часть уравнения (8)
, формирующий левую часть уравнения (8)
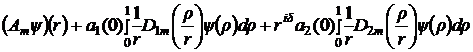 .
.
Лемма 1. Пусть![]() . Тогда существует число
. Тогда существует число ![]() такое, что оператор
такое, что оператор![]() обратим для всех
обратим для всех ![]() .
.
Доказательство. В пространстве![]() рассмотрим оператор
рассмотрим оператор , где
, где ![]() . По теореме Харди-Литтлвуда справедлива оценка
. По теореме Харди-Литтлвуда справедлива оценка  (10).
(10).
Из равенства (9) и свойств многочленов Лежандра следует, что![]() при
при![]() для почти всех
для почти всех![]() . Тогда, используя мажоратную теорему Лебега с учетом оценки (7), получаем, что интеграл в неравенстве (10) стремится к нулю при
. Тогда, используя мажоратную теорему Лебега с учетом оценки (7), получаем, что интеграл в неравенстве (10) стремится к нулю при![]() .Следовательно,
.Следовательно, ![]() . Поэтому существует число
. Поэтому существует число ![]() такое, что
такое, что ![]() для всех
для всех ![]() . Значит, оператор
. Значит, оператор ![]() обратим для всех
обратим для всех ![]() Лемма доказана.
Лемма доказана.
Лемма 2. Пусть ![]() и
и ![]() - число, указанное в лемме 1. Оператор
- число, указанное в лемме 1. Оператор ![]() вида (1) нётеров в пространстве
вида (1) нётеров в пространстве ![]() тогда и только тогда, когда нётеровы в пространстве
тогда и только тогда, когда нётеровы в пространстве ![]() все операторы
все операторы ![]() , причем
, причем 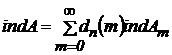 (11)
(11)
Литература:
- Авсянкин О.Г. О С* - алгебре, порожденной многомерными интегральными операторами с однородными ядрами и операторами мультипликативного сдвига [Текст] // Докл. РАН. 2008. Т.419. №6. С.727-728
- Авсянкин О.Г. О С* -алгебре, порожденной многомерными интегральными операторами с однородными ядрами и коэффициентами вида |x|ia[Текст] // Известия вузов. Северо-Кавказский регион. Естеств. науки. 2008.№5. С. 10-14.
- Авсянкин О.Г. О многомерных интегральных операторах с однородными ядрами и осциллирующими радикальными коэффициентами [Текст] // Дифференц. уравнения. 2007. Т.43. №9. С. 1193-1196.
- Авсянкин О.Г., Карапетянц Н.К. Многомерные интегральные операторы с однородными степени (-n) ядрами [Текст] //Докл. РАН. 1999. Т.368. С. 727-729
- Павлов И.В., Скориков А.В. Lp со смешанной нормой на бесконечномерном торе [Текст] //Изв. вузов. Матем. 1986. №2. С 69-72.
- Павлов И.В. О крайних лучах и интегральном представлении в конусе супермартингалов [Текст] //ТВП. 25:3(1980). С. 602-605
- Karapetians N., Samko S. Equations with involute operators// Boston, Basel, Berlin: Birkhauser. 2001.427 p.
- Avsyankin O.G., Karapetians N.K. Multidimensional integral operators with homogenous kernels [Текст] // J. Natur. Geometry. 16(1999).1-18p.
- Михайлов Л.Г., Мухсинов А. Формула представления решений одного трехмерного немодельного сингулярного уравнения в частных производных [Текст] // Докл. РАН. 2010. Т.431. №1, С. 20-21.
- Лаптев А.Г., Бородин Е.Н. Математическая модель процесса адсорбации при очистке сточных вод ТЭС от нефтепродуктов. [Электронный ресурс] //Инженерный вестник Дона. 2010. №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/261 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Кадомцев М.И., Ляпин А.А., Тимофеев С.И. К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт». [Электронный ресурс] // Инженерный вестник Дона. 2012. №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/719 (доступ свободный) – Загл. с экрана. – Яз. рус.